２：形(Form)

点と線

点と線は基本的なジオメトリ(形状)の描画に使用できます。次のサンプルの変数dの値を変更すると、形状を拡大縮小することができます。４つの変数は、dの値にもとづいて位置を設定します。

function setup() {
    const d = 70;
    const p1 = d;
    const p2 = p1 + d;
    const p3 = p2 + d;
    const p4 = p3 + d;

    print("p1 : " + p1); // 70
    print("p2 : " + p2); // 140
    print("p3 : " + p3); // 210
    print("p4 : " + p4); // 280

    createCanvas(400, 400);
    background(0);

    // 緑の線の箱型を描画
    stroke(0, 255, 0);
    line(p3, p3, p2, p3); // (210,210) => (140, 210)への線
    line(p2, p3, p2, p2); // (140,210) => (140, 140)への線
    line(p2, p2, p3, p2); // (140,140) => (210, 140)への線
    line(p3, p2, p3, p3); // (210,140) => (210, 210)への線

    // 白い点を描画
    strokeWeight(4);
    stroke(255);
    point(p1, p1); // (70, 70)
    point(p1, p3); // (70, 210)
    point(p2, p4); // (140, 280)
    point(p3, p1); // (210, 70)
    point(p4, p2); // (280, 140)
    point(p4, p4); // (280, 280)
}

-解説-

point()とline()関数については、「2_2：p5.js 点を描く」と「2_3：p5.js 線、四角形、三角形、長方形を描く」で述べています。

プリミティブなシェイプ(基本的な図形)

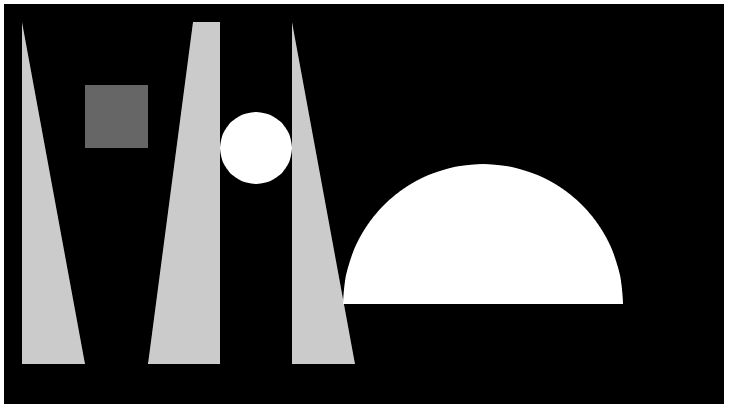
プリミティブなシェイプを作成する関数には、triangle()やrect()、quad()、ellipse()、arc()があります。正方形はrect()から、円はellipse()から作成できます。、これらの関数には、シェイプの位置やサイズを決めるパラメータを渡す必要があります。

function setup() {
    createCanvas(720, 400);
    background(0);
    noStroke();

    fill(204);
    // 三角形を描画
    triangle(18, 18, 18, 360, 81, 360);

    fill(102);
    // 長方形を描画
    rect(81, 81, 63, 63);

    fill(204);
    // 四辺形を描画
    quad(189, 18, 216, 18, 216, 360, 144, 360);

    fill(255);
    // 円を描画
    ellipse(252, 144, 72, 72);

    fill(204);
    // 三角形を描画
    triangle(288, 18, 351, 360, 288, 360);

    fill(255);
    // 円弧を描画
    arc(479, 300, 280, 280, PI, TWO_PI);
}

-解説-

triangle()やrect()、quad()、ellipse()、arc()については、「2_3：p5.js 線、四角形、三角形、長方形を描く」と「2_4：p5.js 楕円(円)、円弧を描く。度とラジアンの扱い。」で述べています。

おまけ：困った顔の作成

次のコードは、基本的なシェイプ関数を使って”困った顔”を描画しようとする例です。図形の位置決めには、方眼紙を使って鉛筆でざっと図形を描いてみる方法が役立ちます。

function setup() {
    createCanvas(400, 400);
    background(0);
    noStroke();

    // 縦長で肌色の楕円 => 顔全体
    fill(255, 204, 204);
    ellipse(200, 200, 300, 340);

    // グレーの三角形２つ => 眉毛
    fill(88);
    triangle(100, 120, 180, 100, 170, 80);
    triangle(220, 100, 300, 120, 230, 80);

    // 白い円２つ => 白目
    fill(255);
    ellipse(150, 150, 30, 30);
    ellipse(250, 150, 30, 30);

    // 黒い円２つ => 黒目
    fill(0);
    ellipse(150, 150, 10, 10);
    ellipse(250, 150, 10, 10);

    // 少し赤い三角形 => 鼻
    fill(255, 149, 175);
    triangle(200, 180, 180, 300, 220, 300);

    // グレーの台形 =>　口ひげ
    fill(88);
    quad(180, 310, 170, 330, 230, 330, 220, 310);

    // 赤い線の円弧 => への字の口
    noFill();
    stroke(255, 0, 0);
    strokeWeight(5);
    arc(200, 380, 60, 80, radians(240), radians(300))
}

円グラフ(パイチャート)

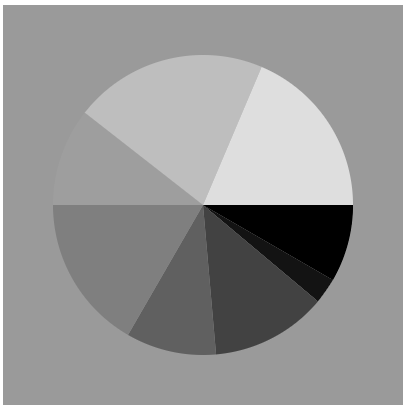
arc()関数を使用すると、配列などに保持したデータから円グラフが作成できます。

const angles = [30, 10, 45, 35, 60, 38, 75, 67];

function setup() {
    createCanvas(400, 400);
    noStroke();
    noLoop();
}

function draw() {
    background(155);
    pieChart(300, angles);
}

function pieChart(diameter, data) {
    let startAngle = 0;
    for (let i = 0; i < data.length; i++) {
        let gray = map(i, 0, data.length, 0, 255);
        fill(gray);
        let stopAngle = startAngle + radians(angles[i]);
        arc(
            width / 2,
            height / 2,
            diameter,
            diameter,
            startAngle,
            stopAngle
        );
        startAngle += radians(angles[i]);
    }
}

-解説-

しかしこの例では、forループを使って複数の円弧を一気に作成しているので、少し分かりづらいかもしれません。次のコードでは分かりやすくするため、１つの円弧を作成する関数を定義し、それを必要な回数だけ呼び出す方法を取っています。またグラフに色付けも行っています。

function setup() {
    createCanvas(400, 400);
    noStroke();
    noLoop();
}

function draw() {
    background(155);
    // // https://www.w3schools.com/colors/colors_names.asp
    // drawPie()関数に、円弧の角度(度数)とカラー名を渡す
    drawPie(30, 'CornflowerBlue');
    drawPie(10, 'DodgerBlue');
    drawPie(45, 'LightCoral');
    drawPie(35, 'Orange');
    drawPie(60, 'NavajoWhite');
    drawPie(38, 'SlateGray');
    drawPie(75, 'Thistle');
    drawPie(67, 'Magenta');
}

// 角度を積算していく開始角度用変数
let startAngle = 0;

// 指定された角度で円弧を描き、色付けする
function drawPie(angle, col) {
    // 渡された角度をラジアン値に変換し、それを開始角度に足して、終了角度とする
    let stopAngle = startAngle + radians(angle);
    // 渡されたカラーで塗る
    fill(col);
    // 開始角度から終了角度まで円弧を描画する
    arc(200, 200, 300, 300, startAngle, stopAngle);
    // 開始角度に、渡された角度を足して次の呼び出しに備える
    startAngle += radians(angle);
}

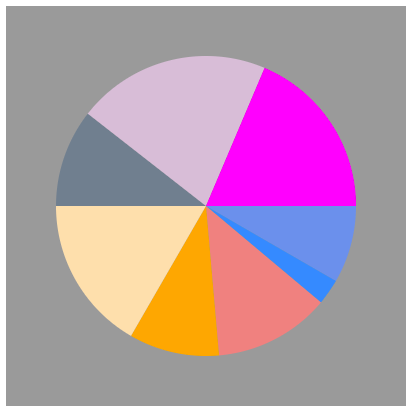
arc()関数で円グラフを描く場合、円の中心座標と円の大きさは一定なので、同じ数値を与えれば事足ります。問題なのは開始角度と終了角度、つまり円の中心からX軸の方向(0度)を基準として、円の何度から何度までのパイ部分を描くのか、の指定です。

arc(x, y, w, h, start, stop, [mode], [detail])

draw()関数内での、最初のdrawPie()関数への呼び出し、drawPie(30, ‘CornflowerBlue’)からは、次のパイが描かれます。

このとき変数startAngleは0なので、0度 + 30度が計算されて、30度がstopAngleに代入されます(実際にはラジアン値)。そして、塗り色がCornflowerBlueに設定され、(200, 200)を中心とする直径300の円が想定されて、その円の0度から30度までのパイ部分がCornflowerBlueで塗られて描かれます。最後、次の呼び出しに備えて、描いたパイ部分だけ、startAngleに足しておきます。これが次の開始角度になります。

正多角形(Regular Polygon)

どんな正多角形が描きたいですか？　五角形それとも六角形、七角形？　違いますか、では二十角形はどうでしょう？　このために作成した次のpolygon()関数はどんな正多角形でも描くことができます。polygon()関数に渡す数値を変えていろいろと試してみてください。

function setup() {
    createCanvas(720, 400);
}

function draw() {
    background(102);

    // 左の三角形に関する座標変換(移動と回転)
    push();
    translate(width * 0.2, height * 0.5);
    rotate(frameCount / 200.0);
    polygon(0, 0, 82, 3);
    pop();

    // 真ん中の二重角形に関する座標変換(移動と回転)
    push();
    translate(width * 0.5, height * 0.5);
    rotate(frameCount / 50.0);
    polygon(0, 0, 80, 20);
    pop();

    // 右の七角形に関する座標変換(移動と回転)
    push();
    translate(width * 0.8, height * 0.5);
    rotate(frameCount / -100.0);
    polygon(0, 0, 70, 7);
    pop();
}

// (x,y)位置と半径、頂点数を受け取り、多角形を描画する
function polygon(x, y, radius, npoints) {
    let angle = TWO_PI / npoints;
    beginShape();
    for (let a = 0; a < TWO_PI; a += angle) {
        let sx = x + cos(a) * radius;
        let sy = y + sin(a) * radius;
        vertex(sx, sy);
    }
    endShape(CLOSE);
}

-解説-

draw()関数内では、作成する正多角形ごとに、push()とpop()関数で囲み、移動と回転の変換を行っています。これにより、その変換がpush()とpop()で囲んだシェイプのみに限定できます。polygon()関数はこのままではいかにも難しそうに見えるので、以下で細かく見ていきます。

function setup() {
    createCanvas(720, 400);
}

function draw() {
    background(102);
    translate(width * 0.5, height * 0.5);
    // 正三角形
    polygon(0, 0, 82, 3);
    // 正二十角形
    //polygon(0, 0, 80, 20);
    // 正七角形
    // polygon(0, 0, 70, 7);
}

function polygon(x, y, radius, npoints) {
    // 等分に刻む角度。正三角形なら 360/3 = 120度
    let angle = TWO_PI / npoints;
    print(degrees(angle));
    // シェイプの描画を開始
    beginShape();
    for (let a = 0; a < TWO_PI; a += angle) {
        // 円周上の座標値(sx, sy)を求める
        // https://himco.jp/2019/02/23/7_6%ef%bc%9a%e5%86%86%e9%81%8b%e5%8b%95-p5-js-javascript/
        let sx = x + cos(a) * radius;
        let sy = y + sin(a) * radius;
        vertex(sx, sy);
    }
    // シェイプの描画を終了
    endShape(CLOSE);

    // 確認用
    // 頂点を少し大きな点で描画する
    for (let a = 0; a < TWO_PI; a += angle) {
        let sx = x + cos(a) * radius;
        let sy = y + sin(a) * radius;
        strokeWeight(10);
        stroke(0);
        point(sx, sy);
        strokeWeight(1);
    }
    // 確認用
    // 多角形を囲む円を描画する
    noFill();
    stroke(255, 0, 0);
    ellipse(0, 0, radius * 2, radius * 2);
    fill(255);
}

上記コードでは、キャンバスのセンターに移動する変換だけを適用しているので、シェイプは重なって描画され、回転しません。draw()内の二十角形と七角形を作成する行にコメントをつけ、正三角形だけを描画すると、次の結果が表示されます。

正三角形は赤い円で囲まれ、頂点には黒い丸がついています。これらは正多角形を作成するpolygon()関数を理解しやすくするために追加しています。

polygon(x, y, radius, npoints)関数

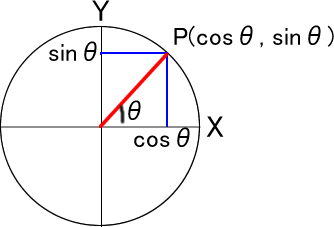
polygon()関数は引数として、正多角形を中に収めるために想定する円の中心座標(x, y)とその半径(radius)、描画したい正多角形の頂点数(npoints)を取ります。polygon(0, 0, 82, 3)の場合には、(0,0)を中心とする半径82の円を想定し正三角形を描け、という意味になります。下図は、これの説明のための図です。

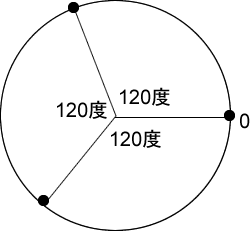
描きたい正三角形の頂点の数は3で、これはpolygon(0, 0, 82, 3)の４つめの引数です。この3で円周の360度を割って、等分に刻む角度とします。360/3は120です。

let angle = TWO_PI / npoints;

そして、(0, 0)を中心とする半径82の円を想定し、円の右端(円の中心からX軸方向に進んだ線と円との交点)を0度として、１つめの頂点とします。ここを起点とし、時計回りに120度進んだ円上の点を２つめの頂点、さらに120度進んだ円上の点を３つめの頂点として、これら３つの頂点を直線で結ぶと、正三角形になります。この３つの頂点を求めているのが、次のforループです。

for (let a = 0; a < TWO_PI; a += angle) {
    // 円周上の座標値(sx, sy)を求める
    let sx = x + cos(a) * radius;
    let sy = y + sin(a) * radius;
    vertex(sx, sy);
}

このsxとsyの計算は、「半径1の円(単位円)の円周上の点(x,y)がx軸の正方向と角度θをなすとき、その座標は(cosθ,sinθ)で表される」という数学の三角関数、サインコサインの定義にもとづいています。ごく簡単に言うと、角度が分かれば、円周上の点の座標(sxとsy)はサインコサインで計算できる、ということです。これが、正多角形の描画に円を想定する理由です。サインコサインと円については「7_6：円運動 p5.js JavaScript」で述べています。

なお、polygon()関数に渡すxとyはどれも0なので、draw()関数内のtranslate(width * 0.5, height * 0.5)による移動先の(360,200)が(0, 0)として扱われます。

星形

この例に特化したstar()関数はさまざまなタイプの星型が作成できます。draw()内のstar()関数の呼び出しにさまざまな数値を入れて、試してみてください。

function setup() {
    createCanvas(720, 400);
}

function draw() {
    background(102);

    push();
    translate(width * 0.2, height * 0.5);
    rotate(frameCount / 200.0);
    star(0, 0, 5, 70, 3);
    pop();

    push();
    translate(width * 0.5, height * 0.5);
    rotate(frameCount / 50.0);
    star(0, 0, 80, 100, 40);
    pop();

    push();
    translate(width * 0.8, height * 0.5);
    rotate(frameCount / -100.0);
    star(0, 0, 30, 70, 5);
    pop();
}

function star(x, y, radius1, radius2, npoints) {
    let angle = TWO_PI / npoints;
    let halfAngle = angle / 2.0;
    beginShape();
    for (let a = 0; a < TWO_PI; a += angle) {
        let sx = x + cos(a) * radius2;
        let sy = y + sin(a) * radius2;
        vertex(sx, sy);
        sx = x + cos(a + halfAngle) * radius1;
        sy = y + sin(a + halfAngle) * radius1;
        vertex(sx, sy);
    }
    endShape(CLOSE);
}

-解説-

では、ここでも星型がどのようにして作られているか、上記コードに手を加えて見ていきましょう。

function setup() {
    createCanvas(720, 400);
}

function draw() {
    background(102);
    translate(width * 0.5, height * 0.5);
    // 頂点数5の星型
    //star(0, 0, 5, 70, 3);
    // 頂点数5の星型
    star(0, 0, 30, 70, 5);
    // 頂点数40の星型
    //star(0, 0, 80, 100, 40);
    noLoop();
}


function star(x, y, radius1, radius2, npoints) {
    // 等分に刻む角度 =>外側の大きな円に使用
    let angle = TWO_PI / npoints;
    // その半分の角度 => 内側の小さな円に使用
    let halfAngle = angle / 2.0;
    beginShape();
    for (let a = 0; a < TWO_PI; a += angle) {
        // 外側の大きな正npoints角形の頂点
        let sx = x + cos(a) * radius2;
        let sy = y + sin(a) * radius2;
        vertex(sx, sy);
        // 内側の小さな正npoints角形の頂点
        // (sx, sy)は、時計回りの方向にhalfAngle分だけずれて、radius1の小さな円周上を移動する
        sx = x + cos(a + halfAngle) * radius1;
        sy = y + sin(a + halfAngle) * radius1;
        vertex(sx, sy);
    }
    endShape(CLOSE);

    // 確認用
    noFill();
    ellipse(0, 0, radius1 * 2);
    ellipse(0, 0, radius2 * 2);
    for (let a = 0; a < TWO_PI; a += angle) {
        let sx = x + cos(a) * radius2;
        let sy = y + sin(a) * radius2;
        strokeWeight(10);
        stroke(0);
        point(sx, sy);
        sx = x + cos(a + halfAngle) * radius1;
        sy = y + sin(a + halfAngle) * radius1;
        point(sx, sy);
        strokeWeight(1);
    }
}

下図の左は、star()関数内に２つあるvertex()への呼び出しを行わない結果で、右は行った結果です。

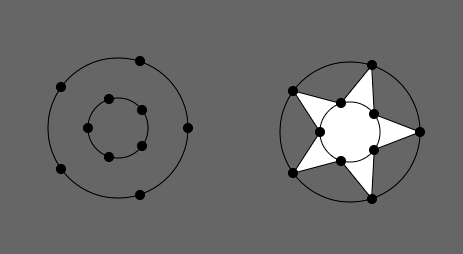
ここでは、星型を作るために、大きな円と小さな円を２つ想定しています。大きな円でも小さな円でも、頂点の座標を求める方法は前の正多角形の方法と変わりませんが、小さな円では、頂点を時計回りの方向にhalfAngle分だけずれるようにしています。大小２つの円上の頂点をforループで一気に作成すると、星型の作成に必要な頂点が得られます。

トライアングルストリップ(接続された一連の三角形)

Ira Greenberg作によるサンプル。vertex()関数とbeginShape(TRIANGLE_STRIP)モードを使って、閉じられたリング(環)を生成します。変数outsideRadiusとinsideRadiusはそれぞれ、リングの半径を制御します。

let x;
let y;
// 外側の円の半径
let outsideRadius = 150;
// 内側の円の半径
let insideRadius = 100;

function setup() {
    createCanvas(720, 400);
    background(204);
    x = width / 2;
    y = height / 2;
}

function draw() {
    background(204);

    let numPoints = int(map(mouseX, 0, width, 6, 60));
    let angle = 0;
    let angleStep = 180.0 / numPoints;

    beginShape(TRIANGLE_STRIP);
    for (let i = 0; i <= numPoints; i++) {
        let px = x + cos(radians(angle)) * outsideRadius;
        let py = y + sin(radians(angle)) * outsideRadius;
        angle += angleStep;
        vertex(px, py);
        px = x + cos(radians(angle)) * insideRadius;
        py = y + sin(radians(angle)) * insideRadius;
        vertex(px, py);
        angle += angleStep;
    }
    endShape();
}

マウスを左右に動かすと、マウスの位置によってリング内に作成される三角形が増減します。

-解説-

beginShape()関数に定数TRIANGLE_STRIPを指定すると、vertex()関数で作成した頂点を結ぶ三角形が描画されます。上記サンプルでは、map()関数を使って、その時点でのマウスのx位置を6から60までの数値に変換し(比の計算)、それを頂点数(numPoints)としています。これにより、マウスが左にあるほど頂点数は少なく、右にあるほど多くなるという、ダイナミックな処理が可能になります。map()関数については「4_7：マッピング(対応付け) p5.js JavaScript」で述べています。

let numPoints = int(map(mouseX, 0, width, 6, 60));

このサンプルのポイントはこれ以降のコードです。以下では、頂点数を取るdrawTriangleStrip()関数を定義して、この処理を見ていきます(引数を固定的に取るので、ダイナミックにはなりません)。

let x;
let y;
// 外側の円の半径
let outsideRadius = 150;
// 内側の円の半径
let insideRadius = 100;

function setup() {
    createCanvas(720, 400);
    background(204);
    x = width / 2;
    y = height / 2;
    noLoop();
    textSize(50);
}

function draw() {
    background(204);
    // 頂点数６個を指定
    drawTriangleStrip(6);
}

// numPointsは頂点の数
function drawTriangleStrip(numPoints) {
    let angle = 0;
    // numPointsが6の場合、angleStepは 360/6/2 = 30
    // 1回のforループで、angleに２回angleStepを足すので、
    // 360.0 / numPointsを2で割る => 180/numPointsと同じ
    let angleStep = 360.0 / numPoints / 2;
    // print(angleStep);

    // 確認用　外側の円と内側の円を実際に描画する
    noFill();
    stroke(255, 0, 0)
    ellipse(x, y, outsideRadius * 2);
    ellipse(x, y, insideRadius * 2)

    fill(255, 120);
    stroke(0)

    // 頂点を共有する一連の接続された三角形
    beginShape(TRIANGLE_STRIP);
    //beginShape();
    for (let i = 0; i <= numPoints; i++) {
        let px1 = x + cos(radians(angle)) * outsideRadius;
        let py1 = y + sin(radians(angle)) * outsideRadius;
        // 外側の円上の頂点を作成
        // 2回め以降は、下の計算でangleStepを足したangleを使って、外側の円周上の頂点を作成
        vertex(px1, py1);
        angle += angleStep;

        // 確認用
        strokeWeight(10);
        point(px1, py1);
        //text(i, px1, py1)

        // 引きつづき、angleStepを足したangleを使って、内側の円周上の頂点を作成
        // => 頂点はangleStep分、時計回りに移動する
        let px2 = x + cos(radians(angle)) * insideRadius;
        let py2 = y + sin(radians(angle)) * insideRadius;
        vertex(px2, py2);
        angle += angleStep;

        // 確認用
        point(px2, py2);
        strokeWeight(1);
        //text(i, px2, py2)
    }
    endShape();
}

これを実行すると、次の結果が得られます。

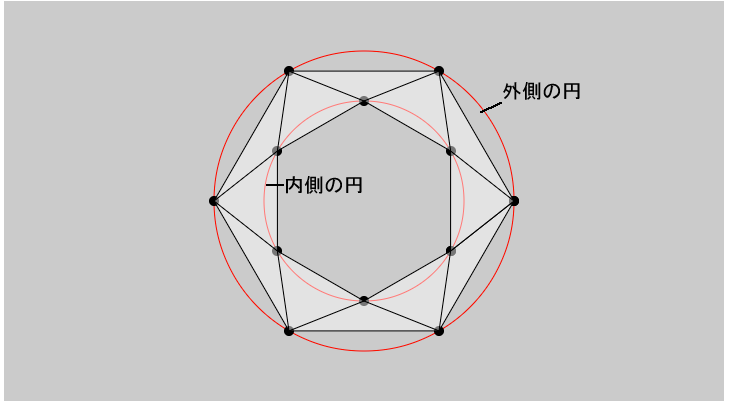
p5.jsのサンプルでリングと呼んでいるのは、上図の大きな円と小さな円にはさまれた部分で、ここに頂点を順に結んだ三角形のストリップが描かれます。ここではdrawTriangleStrip()関数に6を渡しているので、六角形が２つ生成されることになります。

drawTriangleStrip()関数ではまず、ローカル変数angleを0で初期化しています。これは２つの円上に頂点を作成するときの角度になります。次いで、360をnumPoints(今の場合は6)で割り、それを2で割って、ローカル変数angleStepに代入しています。これは増やす角度の分量です。p5.jsのサンプルでは、180をnumPointsで割っていますが、これは360.0 / numPoints / 2と同じことです。下にあるforループでは、1回の繰り返しで2回、angleにangleStepを足しているので、円の全周に合わせるため2で割ります。

let angleStep = 360.0 / numPoints / 2;
let angleStep = 180.0 / numPoints;

その後、参考用に大小２つの円を描画し、drawTriangleStrip()関数の核心であるforループに入っていきます。

ここでもやっていることは、正多角形や星型のときと同じ、sin()とcos()を使った、円上での頂点の作成です。しかし正多角形や星型のサンプルでは、変数aが360度以下であるときにaにangleを足す、というforループであるのに対し、ここでは、

for (let i = 0; i <= numPoints; i++) {　

が使われています。これは、このサンプルではnumPointsをダイナミックに変更するのでこのようにしているのかと思われますが、どちらの方法でも三角形ストリップは描画できます。

またi < numPointsでは、最後の線が描画されないので、<=にする必要があります。下図は、上記コードで２カ所あるtext()関数を実行した結果です。i <= numPointsとすることで、実際にはiが0と6のときに頂点が重複していることが分かります。

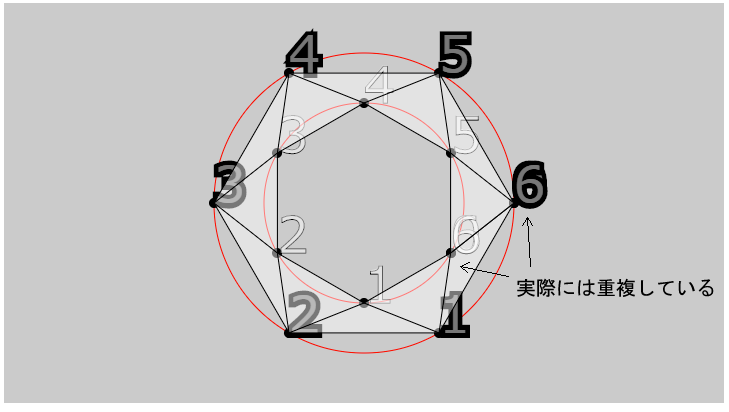
ベジェ曲線

bezier()関数の最初の２つのパラメータはベジェ曲線の最初の点を指定し、最後の２つのパラメータは最後の点を指定します。中央のパラメータは曲線の形状を定義するコントロールポイント(制御点)を設定します。

bezier(x1, y1, cpx1, cpy1, cpx2, cpy2, x2, y2);
学習用ページへのリンク

function setup() {
    createCanvas(720, 400);
    stroke(255);
    noFill();
}

function draw() {
    background(0);
    for (let i = 0; i < 200; i += 20) {
        bezier(
            mouseX - i / 2.0,
            40 + i,
            410,
            20,
            440,
            300,
            240 - i / 16.0,
            300 + i / 8.0
        );
    }
}

マウスを左右に動かすと、描画されるベジェ曲線がダイナミックに変化します。

-解説-

このサンプルで、ベジェ曲線がダイナミックに変化するのは、draw()関数内forループで呼び出しているbezier()関数の引数にmouseXを渡しているからです。

ベジェ曲線については、「ベジェ曲線講座」などで解説されています。ごく簡単に言うと、固定したい点(アンカーポイント)２つと、制御する点(コントロールポイント)２つから、一定の決まりにもとづいて描かれる滑らかな曲線です。

ベジェ曲線は有名な「Adobe Illustrator」やフリーツールの「Inkscape」などの描画アプリケーションで作成できます。

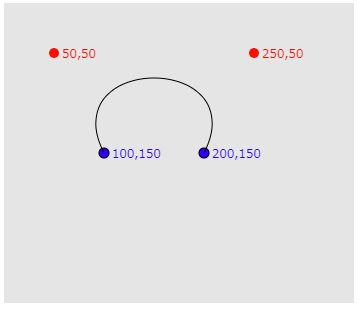
下図はInkscapeで作成した例です。白い丸がコントロールポイントで、青い四角がアンカーポイントです。マウスでコントロールポイントをドラッグすると、コントロールポイントが移動でき、その結果作成される曲線が変化します。

以下は上図のような曲線を作成するbezier()関数の例です。

function setup() {
    createCanvas(350, 300);
    noLoop();
}

function draw() {
    background(230);

    // アンカーポイントを青い円で描画
    // x1, y1, x2, y2 => 開始点と終了点
    fill(0, 0, 255);
    ellipse(100, 150, 10, 10);
    ellipse(200, 150, 10, 10);
    text('100,150', 108, 155);
    text('200,150', 208, 155);

    // コントロールポイントを赤い円で描画
    // cpx1, cpy1, cpx2, cpy2 => ベジェ曲線を制御する点
    noStroke();
    fill(255, 0, 0);
    ellipse(50, 50, 10, 10);
    ellipse(250, 50, 10, 10);
    text('50,50', 58, 55);
    text('250,50', 258, 55);

    // ベジェ曲線を黒い線で描画
    noFill();
    stroke(0);
    bezier(100, 150, 50, 50, 250, 50, 200, 150)
}

下図はこの実行結果です。アンカーポイントやコントロールポイントをドラッグできるようにすると、ダイナミックに変化するベジェ曲線が描画できます。

3D プリミティブ

3Dオブジェクトを数学的な方法で疑似空間に配置します。box()とsphere()関数は、サイズの指定に最低でも１つのパラメータを取ります。作成したシェイプはtranslate()関数によって位置取りできます。

function setup() {
    createCanvas(710, 400, WEBGL);
}

function draw() {
    background(100);

    noStroke();
    fill(50);
    push();
    translate(-275, 175);
    rotateY(1.25);
    rotateX(-0.9);
    box(100);
    pop();

    noFill();
    stroke(255);
    push();
    translate(500, height * 0.35, -200);
    sphere(300);
    pop();
}

下図はこの実行結果です。

-解説-

とはいえこれでは面白くないので、もう少し3Dが実感できる例を紹介します。

function setup() {
    createCanvas(500, 500, WEBGL);
    angleMode(DEGREES);
    // デバッグモードにする
    debugMode();
}

function draw() {
    background(200);
    // 画面をぐりぐりできるようにする
    orbitControl();
    // 3Dオブジェクトを作成する
    box(); // 直方体
    cone(); // 円錐
    torus(); //　円環
}

マウスでグリグリできます。

3D空間を作成するには、createCanvas()関数の第３引数に定数WEBGLを指定します。debugMode()関数はデバッグモードを有効にします。これにより、3D空間に地面のグリッドと、X、Y、Zの３軸の向きを示すカラーの線が描画されるようになります。またorbitControl()関数でマウスのドラッグによる3D空間の制御が可能になります。

p5.jsで3Dを始めたいときには「Getting started with WebGL in p5」が参考になります。