Pathfinding(パスファインディング)とは、パスをファインドすること、つまり目的地までの経路を見つけることで、一般的には「ある場所から他の場所に移動するときの最短経路を導き出す方法」を言います。
その導き出し方(アルゴリズム)はいくつもあり(「最短経路問題」)、最も有名なのが「A*(A-star, エースター)探索アルゴリズム」です。ただしどの方法もそうやすやすと始められる代物ではありません。
本稿では、最も取り組みやすそうな「幅優先探索アルゴリズム」をp5.jsで実装する方法を見ていきます。
以下は「A basic pathfinding algorithm (implemented in Javascript)」(基本的な経路探索アルゴリズム(JavaScriptによる実装))ページに記載されている記事の翻訳です。
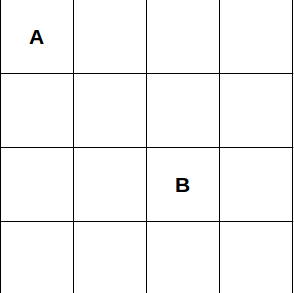
こんな状況を思い浮かべてみてください。みなさんは2次元のボードにある”A”という名前の付いた正方形の上にいて、”B”という名前の正方形までの最短経路を見つける必要があり、この地図が与えられています。
さほど難しくはありませんね。人間なので、正方形”A”から”B”への最適な経路はいくつか簡単に見つけることができます(0.5秒もかからないうちに)。
ではもう少し複雑な場合はどうでしょう? 次のような場合です。

(少し)難しいですが、ほどなく解けるでしょう。しかし障害物がもっと多いと、問題の解決にはもっと多くの努力が要るでしょう。
とは言え、コンピュータはごく単純なアルゴリズムでこれが解決でき、さらに気が遠くなるほど難しい経路探索(パスファインディング)問題すらも解決できることが分かっています。以下ではこのアルゴリズムの書き方を学んでいきます。
目次
基本的な経路探索アルゴリズム(JavaScriptによる記述)
使用するのは「幅優先探索(Breadth-First Search)」と呼ばれる手法です。
Googleで調べてみても構いませんが、基本的には、通ることのできる長さが1の経路を全部調べ、次に通るのことのできる長さが2の経路を全部調べるということを、正方形”A”から”B”への最短経路が見つかるまでつづけるという方法です。
これは言うほど非効率的ではありません(非常に大きな経路探索問題も、今時のコンピュータが実行不可能だと音を上げる前に解決するでしょう)が、覚えておいていただきたいのは、この手法を使った経路探索問題の解決に必要なメモリと時間は、ボードのサイズが大きくなるにつれ、比較的急速に増大する、ということです。
ステップ1:キューが要る
まず必要なのは、最適な経路決定のために調べる正方形全部を追跡するキュー(待ち行列)のデータ構造です。これは経路に順位付けをする”to-do”リストと考えてください。
キュー(queue)は”待ち行列”と訳され、FIFO(先入れ先出し)の方法でデータを扱います。
// "キュー"データ構造は配列を使ってシミュレーションする
var q = [];
// * 上級レベルの読者へ:このキューは技術的に言って、リンク付けしたリストを実装する方が高速になる。しかしこの方がよりシンプル。ステップ2:新しい位置を”発見した”とき、それをキューに追加する必要がある
キューは探索する位置の”to-do”リストのようなものだということを思い出してください。そして探索は最も近い位置から始めます(これは、近い位置は遠い場所よりも先にキューに追加するということです)
では、ボード上でスタート位置に最も近いのはどの位置でしょう? これはひっかけ問題です。最も近いのはスタート位置です。したがって、このスタート位置をキューに入れることから始めます。
ステップ3:探索開始!
探索は次の流れで進めます:
- キューから最初の位置を取り出す
- キューから取り出した位置から1だけ”移動”した位置を走査する(この例では、現在のタイルの北と南、東、西にあるタイル)
- これらの位置の1つが目的地なら、終了!
- そうでない場合;まだ調べていなくて有効な位置(つまりボード上にあり”障害物”でない位置)なら、その新しい位置をキューの末尾に追加する
- この過程を繰り返す(キューから最初の位置を取り出す…)
探索は、目的地の状態が見つかるか(上記の3)、探索する位置がなくなる(キューが空になる)までつづけます。
目的地が見つかった場合には、その最短経路が答えだと分かります(つねに最も近い位置を最初に追加しているので、それが最短経路だと分かります)。
探索する位置がなくなった場合には、それは、終了位置までの有効な経路がなかったということです(キューが空になったということは、探索する有効な位置がなくなったということです)
上記の手順を進めるとこの結果になる、ということはもう十分お分かりかも知れませんが、すっきりしない方のために(ただ文字を追っているだけなので無理からぬことです)、具体的な例を見ていきましょう。
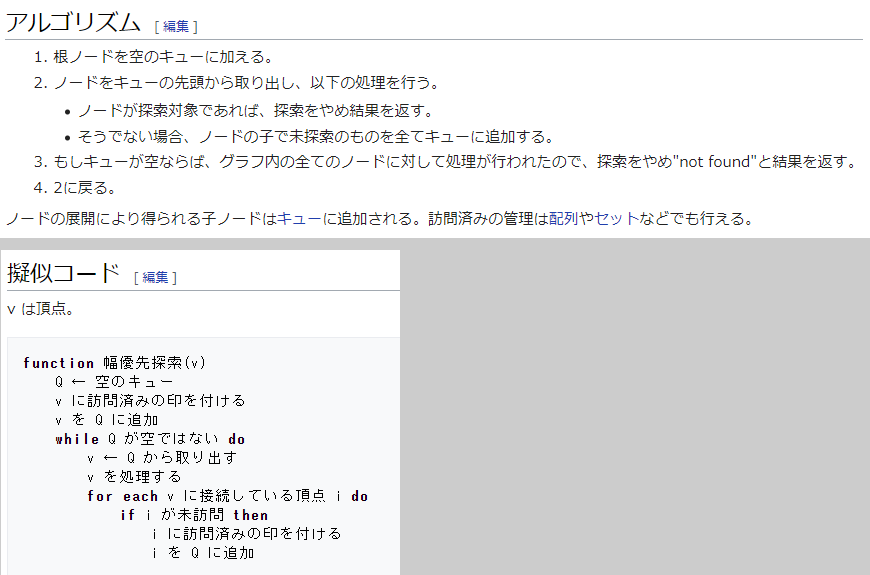
参考;下図は上記「幅優先探索」ページに掲載されているアルゴリズムと疑似コードです。
クィックサンプル:アルゴリズムを1つずつ見ていく
上の例を再利用して、位置”A”から位置”B”に行きたいとします。この(実にシンプルな)問題をここまで見てきたアルゴリズムを使って解決してみましょう。

ステップ1:キューが要る。これはJavaScriptの配列で表す
Queue = []
ステップ2:スタート位置をキューに追加する必要がある
位置は座標として次のように表すことにします。
(上端からの距離、左端からの距離)
Queue = [(0,0)]
ステップ3:サブステップの流れ通りに…
- キューから最初の位置を取り出す:
- 位置: (0,0), Queue = []
- この位置周辺を走査する:
- 北: 無効(グリッド上端外)
- 東: 新しい位置: (0,1), Queue: [ (0,1) ]
- 南: 新しい位置: (1,0), Queue: [ (0,1), (1,0) ]
- 西: 無効(グリッド左端外)
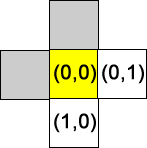
- この過程を繰り返す(変化のあるときにキューの状態を示しています:
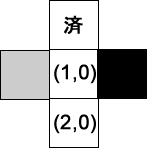
- キューから次の位置を得る…位置: (0,1), Queue = [ (1,0) ]
- キューに近隣の有効な位置を追加する…Queue = [ (1,0), (0,2) ]
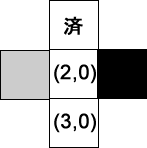
- キューから次の位置を得る…位置: (1,0), Queue = [ (0,2) ]
- キューに近隣の有効な位置を追加する…Queue = [ (0,2), (2,0) ]
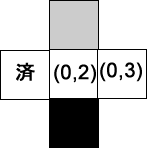
- キューから次の位置を得る…位置: (0,2), Queue = [ (2,0) ]
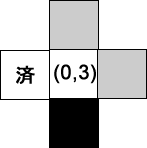
- キューに近隣の有効な位置を追加する…Queue = [ (2,0), (0,3) ]
- キューから次の位置を得る…位置: (2,0), Queue = [ (0,3) ]
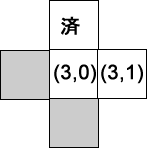
- キューに近隣の有効な位置を追加する…Queue = [ (0,3), (3,0) ]
- キューから次の位置を得る…位置: (0,3), Queue = [ (3,0) ]
- キューに近隣の有効な位置を追加する…Queue = [ (3,0) ](右上隅には、有効で未訪問な近隣位置がないので、キューには何も追加しない)
- キューから次の位置を得る…位置: (3,0), Queue = [ ]
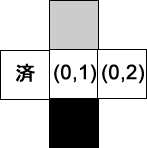
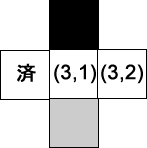
- キューに近隣の有効な位置を追加する…Queue = [ (3,1) ]
- キューから次の位置を得る…位置: (3,1), Queue = [ ]
- キューに近隣の有効な位置を追加する…Queue = [ (3,2) ]
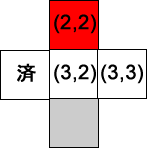
- キューから次の位置を得る…位置: (3,2), Queue = [ ]
- 最後! (3,2)の正方形に隣接する有効な位置を追加するとき、(2,2)が目的地であることを知るので、アルゴリズムは停止する。これで位置Aと位置B間の最短経路を見つけることができた
コードにする
では、”グリッド”をコードにするとどのように見えるかをやってみましょう。
// 4 x 4 グリッド
// このグリッドは2次元配列で表す
var gridSize = 4;
var grid = [];
for (var i = 0; i < gridSize; i++) {
grid[i] = [];
for (var j = 0; j < gridSize; j++) {
grid[i][j] = 'Empty';
}
}
// 最初のインデックスは"上端の行からの距離"
// 2つめのインデックスは"左端の列からの距離"
// 上記の障害物はこのように表す
grid[0][0] = "Start";
grid[2][2] = "Goal";
grid[1][1] = "Obstacle";
grid[1][2] = "Obstacle";
grid[1][3] = "Obstacle";
grid[2][1] = "Obstacle";“グリッド”を表すことができたので、スタート位置とボード配列を取り、最短経路の配列を返す関数を記述しましょう(そして全部をひとまとめにします)。
注意:実際に最短経路を返すにはもう少し複雑になります(この後分かります)。しかし、その根幹では、ここまで述べてきたアルゴリズムをただ実装しているにすぎないことが分かります。
// スタート位置は次の形式:
// [distanceFromTop, distanceFromLeft]
var findShortestPath = function(startCoordinates, grid) {
var distanceFromTop = startCoordinates[0];
var distanceFromLeft = startCoordinates[1];
// 各"location"はその座標と、到達に必要な最短経路を保持する
var location = {
distanceFromTop: distanceFromTop,
distanceFromLeft: distanceFromLeft,
path: [],
status: 'Start'
};
// 内部にすでにスタート位置を持っているlocationでqueueを初期化
var queue = [location];
// グリッドを繰り返し処理して目的地を探索する
while (queue.length > 0) {
// キューから最初の位置を取る
var currentLocation = queue.shift();
// 北を調べる
var newLocation = exploreInDirection(currentLocation, 'North', grid);
if (newLocation.status === 'Goal') {
return newLocation.path;
}
else if (newLocation.status === 'Valid') {
queue.push(newLocation);
}
// 東を調べる
var newLocation = exploreInDirection(currentLocation, 'East', grid);
if (newLocation.status === 'Goal') {
return newLocation.path;
}
else if (newLocation.status === 'Valid') {
queue.push(newLocation);
}
// 南を調べる
var newLocation = exploreInDirection(currentLocation, 'South', grid);
if (newLocation.status === 'Goal') {
return newLocation.path;
}
else if (newLocation.status === 'Valid') {
queue.push(newLocation);
}
// 西を調べる
var newLocation = exploreInDirection(currentLocation, 'West', grid);
if (newLocation.status === 'Goal') {
return newLocation.path;
}
else if (newLocation.status === 'Valid') {
queue.push(newLocation);
}
}
// 有効な経路は見つからなかった
return false;
};
// locationのstatusを調べる関数
// (グリッド上にあり、"obstacle"でなく、アルゴリズムが未チェックなら"valid")
// "Valid"か "Invalid"、"Blocked"または"Goal"を返す
var locationStatus = function(location, grid) {
var gridSize = grid.length;
var dft = location.distanceFromTop;
var dfl = location.distanceFromLeft;
if (location.distanceFromLeft < 0 ||
location.distanceFromLeft >= gridSize ||
location.distanceFromTop < 0 ||
location.distanceFromTop >= gridSize) {
// locationはグリッド上にないので'Invalid'を返す
return 'Invalid';
}
else if (grid[dft][dfl] === 'Goal') {
return 'Goal';
}
else if (grid[dft][dfl] !== 'Empty') {
// locationは障害物か既にチェックしたかのどちらか
return 'Blocked';
}
else {
return 'Valid';
}
};
// 指定された位置から指定された方向にグリッドを調べる
var exploreInDirection = function(currentLocation, direction, grid) {
var newPath = currentLocation.path.slice();
newPath.push(direction);
var dft = currentLocation.distanceFromTop;
var dfl = currentLocation.distanceFromLeft;
if (direction === 'North') {
dft -= 1;
}
else if (direction === 'East') {
dfl += 1;
}
else if (direction === 'South') {
dft += 1;
}
else if (direction === 'West') {
dfl -= 1;
}
var newLocation = {
distanceFromTop: dft,
distanceFromLeft: dfl,
path: newPath,
status: 'Unknown'
};
newLocation.status = locationStatus(newLocation, grid);
// この新しい位置が有効なら、'Visited'の印をつける
if (newLocation.status === 'Valid') {
grid[newLocation.distanceFromTop][newLocation.distanceFromLeft] = 'Visited';
}
return newLocation;
};
// 必要な関数が定義できたので、最短経路の取得を実行!
// 4 x 4 グリッド
// このグリッドは2次元配列で表す
var gridSize = 4;
var grid = [];
for (var i = 0; i < gridSize; i++) {
grid[i] = [];
for (var j = 0; j < gridSize; j++) {
grid[i][j] = 'Empty';
}
}
// 最初のインデックスは"上端の行からの距離"
// 2つめのインデックスは"左端の列からの距離"
// 上記の障害物はこのように表す
grid[0][0] = "Start";
grid[2][2] = "Goal";
grid[1][1] = "Obstacle";
grid[1][2] = "Obstacle";
grid[1][3] = "Obstacle";
grid[2][1] = "Obstacle";
console.log(findShortestPath([0, 0], grid));ハードルが少し高いかも知れませんが、コードをコピーして、ブラウザのコンソールにペーストするか、Node.jsを使って実行すると、最短経路が次のように表示されることが分かります。
‘South’, ‘South’, ‘South’, ‘East’, ‘East’, ‘North’
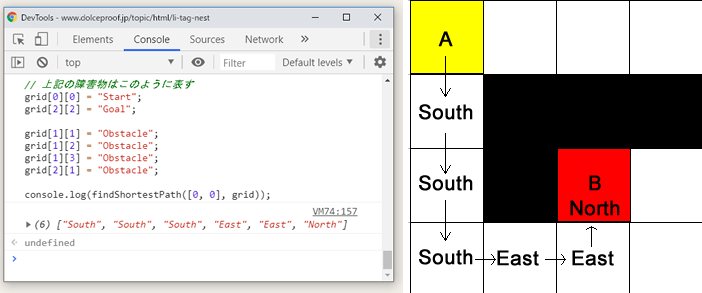
何より重要なのは、非常に複雑な経路探索問題であっても、目的地までの最短経路を高速で計算できることです。