目次
配列
配列はデータのリストです。配列に含まれるそれぞれのデータは、配列内での位置を表すインデックス番号によって識別されます。配列はゼロベースです(0から数え始める)。これは、配列の最初の要素は[0]として、2つめの要素は[1]として参照する、ということを意味します。次のサンプルでは、coswaveと名付けた配列にコサイン値を入れています。このデータは画面上に3つの異なる方法で表示されます。
let coswave = [];
function setup() {
createCanvas(720, 360);
for (let i = 0; i < width; i++) {
let amount = map(i, 0, width, 0, PI);
coswave[i] = abs(cos(amount));
}
background(255);
noLoop();
}
function draw() {
let y1 = 0;
let y2 = height / 3;
for (let i = 0; i < width; i += 3) {
stroke(coswave[i] * 255);
line(i, y1, i, y2);
}
y1 = y2;
y2 = y1 + y1;
for (let i = 0; i < width; i += 3) {
stroke((coswave[i] * 255) / 4);
line(i, y1, i, y2);
}
y1 = y2;
y2 = height;
for (let i = 0; i < width; i += 3) {
stroke(255 - coswave[i] * 255);
line(i, y1, i, y2);
}
}このサンプルを実行すると、次の結果が表示されます。

解説
上記サンプルの変数coswaveをprint()関数で出力すると、1以下の小さな数値の要素を720個持つ配列であることが分かります。上記コードではこの小さな数値を使って、上図に見られる3つの帯状の描画を作り出しています。このコードを見ただけですぐ理解できる方はそれでよいでしょうが、そんな方はごく少数でしょう。
三角関数の理解や扱いは簡単ではありませんが、滑らかな変化が欲しい場合に役立ちます。以降では、配列よりもこの、滑らかに変化する小さな数値を中心に見ていくことにします。
視覚化
配列coswaveが要素として持つ小さな数値がどのようなものか(coswaveは配列なので、要素の並びの順番も重要です)を理解するために、グラフで表してみます。そのために以降では、Plotly.jsというグラフの描画に便利なJavaScriptライブラリを使用します。
次のHTMLコードは、Plotly.jsの読み込みと、グラフの描画に必要なJavaScriptファイルの読み込み、CSS、HTML要素の定義の要領を示しています。
<!doctype html>
<html lang="ja">
<head>
<meta charset="UTF-8">
<title>p5.js Examples</title>
<script src="https://cdnjs.cloudflare.com/ajax/libs/p5.js/0.8.0/p5.min.js"></script>
<!-- Plotly.jsを読み込む -->
<script src="https://cdn.plot.ly/plotly-latest.min.js"></script>
<!-- グラフ描画用のJavaScriptファイルを読み込む -->
<script src="js/graph.js"></script>
<!-- グラフを描画する領域を定めるCSS -->
<style>
.graph-area {
margin: 10px;
width: 500px;
height: 500px;
border: 1px solid black;
}
.container {
display: flex;
}
</style>
</head>
<body>
<script src="sketch.js"></script>
<!-- グラフを描画する<div>要素 -->
<div id="chart" class="graph-area"></div>
</body>
</html>グラフを描画する次の関数plot()はgraph.jsファイルに記述し、jsフォルダ内に置きます、
// Plotlyを使ってグラフを描く
function plot(xArray, yArray) {
const trace = {
x: xArray,
y: yArray,
type: 'scatter'
};
const data = [trace];
const layout = {
xaxis: {
range: [0, 800],
title: 'i値'
},
yaxis: {
range: [-1, 1],
title: 'cosValue'
}
};
Plotly.newPlot('chart', data, layout, {
displayModeBar: false
});
}sketch.jsは次のように修正します。
// コサイン波用配列
const coswave = [];
function setup() {
createCanvas(720, 360);
// グラフの描画に使用するi値の配列
const iArray = [];
// iを0から720未満(719)まで1ずつ大きくする
for (let i = 0; i < width; i++) {
// サンプルのコード
// let amount = map(i, 0, width, 0, PI);
// coswave[i] = abs(cos(amount));
// 分かりやすいようにPIを180に置き換え、変換も1つずつ行う
let amount = map(i, 0, width, 0, 180);
// print(amount)// => 0, 0.25, 0.5,..., 179.5, 179.75という、0から179.75まで0.25ずつ大きくなる数値
// cos()関数に渡すのでラジアン値に変換
let radian = radians(amount);
let cosValue = cos(radian);
// cosValueは全部正の数にしたい。
// 負の数があるので、絶対値に変換
cosValue = abs(cosValue);
// 配列coswaveに追加
coswave.push(cosValue);
// i値を追加
iArray.push(i);
}
background(255);
noLoop();
// cosValueはどのような値なのかを確認するためにグラフに描画する
plot(iArray, coswave);
// print(coswave);
//print(coswave.length); // 720
}
function draw() {
let y1 = 0;
let y2 = height / 3; // 120
for (let i = 0; i < width; i += 3) {
// たとえば、1に近い0.9は、0.9*255=229.5 => 白に近い
// 0に近い0.1は、0.1*255=25.5 => 黒に近い
// => 左か右に行くほど白く、真ん中ほど黒に近いグラデーションになる。
stroke(coswave[i] * 255);
// (i,0)から(i, 120)まで線を描く
line(i, y1, i, y2);
}
y1 = y2; // 120
y2 = y1 + y1; // 240
for (let i = 0; i < width; i += 3) {
// 1つめのグラデーションの数値を4で割るので、変化の度合いが弱まり黒に近くなる
stroke((coswave[i] * 255) / 4);
// (i,120)から(i, 240)まで線を描く
line(i, y1, i, y2);
}
y1 = y2; // 240
y2 = height; // 360
for (let i = 0; i < width; i += 3) {
// 255から引くので、白黒が反転することになる
// => 1つめと白黒が反転したグラデーションになる
stroke(255 - coswave[i] * 255);
// (i,240)から(i, 360)まで線を描く
line(i, y1, i, y2);
}
}このコードを実行すると、下図のグラフが描画できます。グラフ上をマウスでなぞると、Plotly.jsの機能によって、曲線のXとY値がキャンバスに表示されます。。
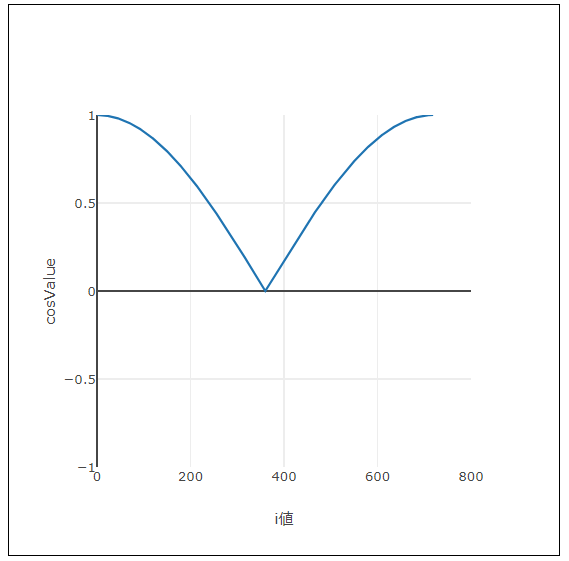
グラフから分かることは、Xが0のときYは1で、そこからXが大きくなるにつれてYは滑らかに小さくなり、Xが360のときにYはほぼ0になってここで反転して大きくなり、Xが719のときほぼ1になる、ということです。上記サンプルではこのように変化する数値を持つ配列を作り出しているのです。
上記コードのsetup()内のforループでは、サンプルでは2行で表されているコードを、分かりやすいように次のように置き換えています。
// サンプルのコード
// let amount = map(i, 0, width, 0, PI);
// coswave[i] = abs(cos(amount));
// 分かりやすいようにPIを180に置き換え、変換も1つずつ行う
let amount = map(i, 0, width, 0, 180);
// print(amount)// => 0, 0.25, 0.5,..., 179.5, 179.75という、0から179.75まで0.25ずつ大きくなる数値
// cos()関数に渡すのでラジアン値に変換
let radian = radians(amount);
let cosValue = cos(radian);
// cosValueは全部正の数にしたい。
// 負の数があるので、絶対値に変換
cosValue = abs(cosValue);
// 配列coswaveに追加
coswave.push(cosValue);map()はp5.jsの便利な関数で、比の計算を行います。
幅が720のときの位置0は、角度が360度のとき何度に相当するか?
0 : 720 = x : 360 => 720x = 0 => x = 0 => xは0
同様に位置1と2は何度に相当するか?
1 : 720 = x : 360 => 720x = 360 => x = 0.5 => xは0.5
2 : 720 = x : 360 => 720x = 360 * 2 = x = 1 => xは1
draw()関数では、coswave配列を使って、3つの帯を描きます。ここでは帯の位置をずらすためにletで宣言した変数(つまり上書きできる)のy1とy2が賢く利用されています。もちろん、個別の固定的な変数(const)を使うこともできます。
// 上の帯
let y1 = 0;
let y2 = height / 3; // 120
// 真ん中の帯
y1 = y2; // 120
y2 = y1 + y1; // 240
// 下の帯
y1 = y2; // 240
y2 = height; // 360上の帯は白からだんだん黒くなり、また白くなっていきます。これは、coswaveの数値に255を掛けた結果をstroke()関数に与えることで実現されています。たとえば1は1*255で白になり、0.9は0.9*255で、少し黒に近くなります。coswaveには上記グラフで見たように滑らかに小さくなって大きくなる数値が並んでいるので、帯の色もそのように見えることになります。
真ん中の帯では、白から黒、黒から白にだんだん変化する数値を使っていますが、4で割っているので、値自体が小さくなります。これは変化の度合いが弱まり、全体が黒に近くなることを意味します。
下の帯では、coswaveの数値に255掛けたものを、255から引いています。これによりたとえばcoswaveの1は1*255=255が255から引かれ0に、0.9は0.9*255=229.5が255から引かれ25.5になります。これは256個の階調で表される白の度合いを黒の度合いに、黒の度合いを白の度合いに変換する操作です。この計算によって、下の帯は上の帯とまったく逆の白さ加減、黒さ加減で描かれることになります。
2次元配列
2次元(2D)配列を作成するシンタックスを例で示します。2次元配列の値には、2つのインデックス値を通してアクセスします。2次元配列はイメージの保持に役立ちます。次のサンプルの各点の濃度は、イメージのセンターからの距離に関連付けて決めています。
let distances = [];
let maxDistance;
let spacer;
function setup() {
createCanvas(720, 360);
maxDistance = dist(width / 2, height / 2, width, height);
for (let x = 0; x < width; x++) {
distances[x] = []; // ネストされた配列を作成
for (let y = 0; y < height; y++) {
let distance = dist(width / 2, height / 2, x, y);
distances[x][y] = (distance / maxDistance) * 255;
}
}
spacer = 10;
noLoop();
}
function draw() {
background(0);
// この埋め込み(2重)ループは、spacer変数の値にもとづいて、
// 配列の値をスキップ(飛ばす)ので、配列には、ここで描画されるよりも
// 多くの値がある。spacer変数の値を変更すると、点の密度を変えることができる。
for (let x = 0; x < width; x += spacer) {
for (let y = 0; y < height; y += spacer) {
stroke(distances[x][y]);
point(x + spacer / 2, y + spacer / 2);
//point(x + spacer / 2, y + spacer / 2);
// 結果を明瞭にするため、点を円に変更
ellipse(x + spacer / 2, y + spacer / 2, 1);
}
}
}下図はこの実行結果です。キャンバスのセンター辺りが、ちょうどブラックホールのように、ぼんやりと黒くなっているように見えます。

解説
2次元配列は、要素として配列を持つ配列のことで、このサンプルでは変数distancesが2次元配列です。distancesは要素を720個持ち、その要素である配列がそれぞれ、360個の数値を要素として持っています。
// distances配列は要素を720個持っている。
// その各要素は配列で、それぞれが360個の数値を持っている。
// [[255,254,717,252.435,...],[],...[]]
print(distances);下図はdistancesの出力結果です。ここからは、たとえばdistances配列の最初の要素の配列(distances[0])は、255, 254.71729699588303, 254.43585744850418, 254.15568555513374といった数値を持っていること分かります。

2次元配列distancesを調べる
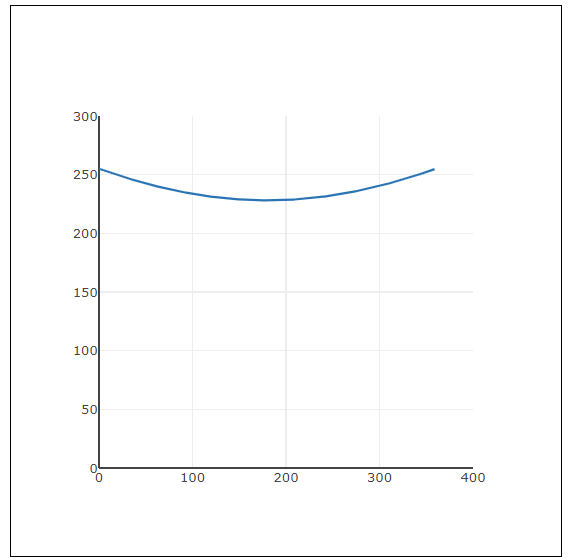
ではこのdistances[0]が持つ数値はどのようなものなのでしょう? 数値の数が360個と多く、またそれぞれに微小な違いしかないようなので、これもグラフ化してみます。すると、下図の結果で示すように、255からスタートして次第に小さくなり、真ん中辺りで反転して次第に255辺りまで大きくなる数値の並びであることが分かります。
function setup() {
createCanvas(720, 360);
maxDistance = dist(width / 2, height / 2, width, height);
// x値を保持する配列
let xData = [];
for (let x = 0; x < width; x++) {
distances[x] = []; // ネストされた配列を作成
// x値を追加
xData.push(x);
for (let y = 0; y < height; y++) {
let distance = dist(width / 2, height / 2, x, y);
distances[x][y] = (distance / maxDistance) * 255;
}
}
spacer = 10;
noLoop();
// distances[0]の数値をグラフで視覚化してみる
plot(xData, distances[0]); // => 両端が高く、真ん中が低く見える曲線
}
つづいて、distances[0]以降の配列、つまりdistances[1]やdistances[2]…などがどんな数値を持っているかをグラフで見てみましょう。なおこのためには、既存のグラフに追加するPlotly.addTraces()を使った関数addPlot()をgraph.jsに定義しておきます。
// distances[0]以降の配列が持つ数値もグラフ化してみる
// 両端がより下がり、真ん中が下によりくびれて見える曲線
// 曲線は実は2本がほぼ重なっている(似た数値を持つ配列が2つある)
for (let i = 1; i < width; i += 20) {
addPlot(distances[i]);
}
// graph.jsに新たに定義
function addPlot(yArray) {
Plotly.addTraces('chart', { y: yArray });
}下図はこの結果です。描かれる曲線は次第に下に移り、真ん中辺りのくびれが大きくなっていくように見えます。
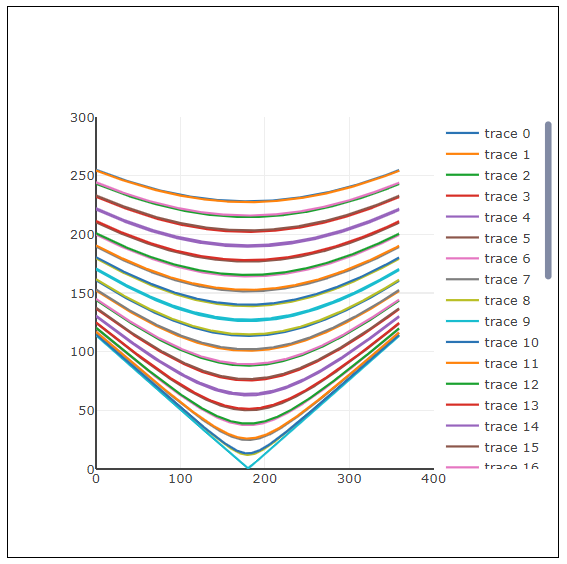
そして注意が必要なのは、ここで描かれている曲線は実はほとんどが2本ずつ重なっているように見えている、ということです。これは曲線にマウスを重ねることで表示される、曲線ごとの具体的な数値を見ても分かります。描かれる曲線はtrace0からスタートし、trace1,2と下に移動しますが、trace26で反転して以降上に移動しています。
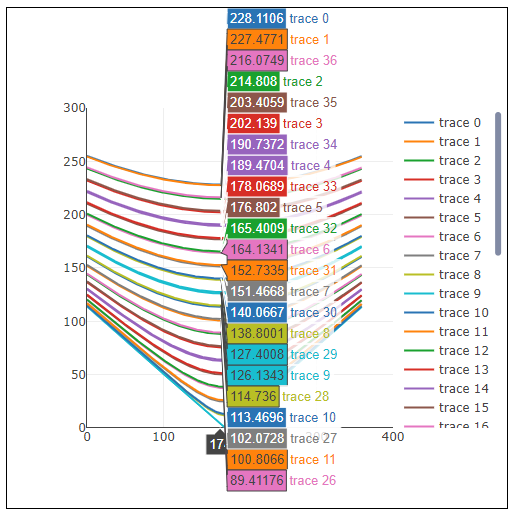
distances2次元配列のこうした数値の並びを利用しているのが、draw()関数内のforループのstroke()関数です。ここでは、spacer分だけ右に進むたびにspacer分だけ下に進んで、distances配列の配列から数値を取り出し、それをstroke()に指定しています。
// spacer分だけ右に進むたびにspacer分だけ下に進む
for (let x = 0; x < width; x += spacer) {
for (let y = 0; y < height; y += spacer) {
stroke(distances[x][y]);
ellipse(x + spacer / 2, y + spacer / 2, 1);
}
}たとえば変数xが小さいうちは、distances[x]によって、distances配列に含まれる初めの方の配列が選ばれます。これは下図左に示すような、くびれの小さな曲線で表される数値の並びです。これをstroke()関数に与えると、白から始まり少しだけグレーがかるものの、また白近くに戻るという濃度変化が生まれます。
同様に、変数xがループの中頃に来ると、distances配列に含まれる中頃の配列が選ばれます。これは下図右に示すようなくびれの大きな曲線で現れる数値の並びです。これをstroke()関数に与えると、グレーから始まり、大きな変化の度合いで黒に近づきまたグレーに戻るという濃度変化が生まれます。
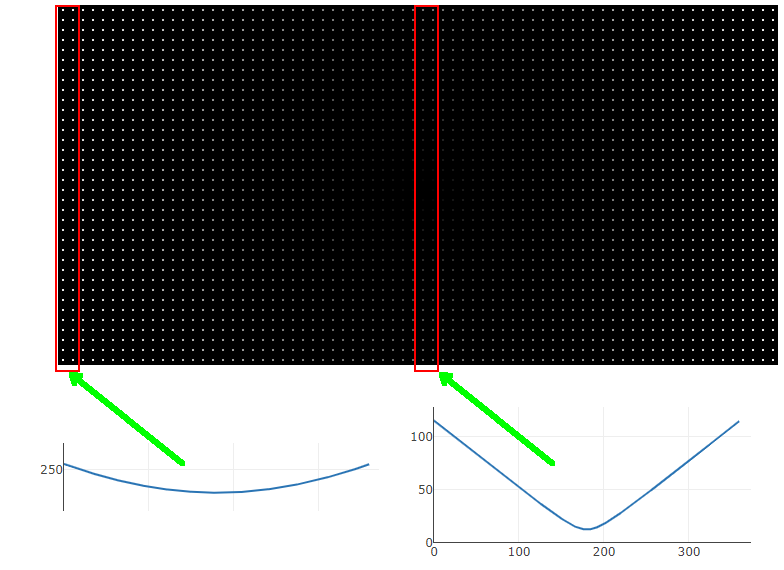
distances配列の数値の作り方
では、上で見たくびれた曲線で表される数値はどうやって作成されているのでしょう?
ここではまず、キャンバスのセンターから右下隅までの距離(maxDistance)を求めています。
// キャンバスの中央から右下隅までの長さ
maxDistance = dist(width / 2, height / 2, width, height);そして、キャンバスセンターから、キャンバスの全ピクセルの座標((0,0),(0,1),(0,2)…)までの距離(distance)を求め、maxDistanceに対する比率を計算して、それに255を掛けています。255を掛けることで、比率を255を最大値とする数値に置き換えることができます。これによって、maxDistanceに近いものほど255に近く、maxDistanceに近くないほど255に近くなくなります。
// xは0から720未満まで
for (let x = 0; x < width; x++) {
distances[x] = [];
// yは0から360未満まで
for (let y = 0; y < height; y++) {
// キャンバスの中央から(x, y)までの距離
let distance = dist(width / 2, height / 2, x, y);
// distanceのmaxDistanceに対する比率(0.99や0.98など)
// それに255を掛けると、各距離を、最大が255の数値に置き換えることができる。
// その数値をdistances2次元配列の[x][y]番めの配列の値に設定
// => 720行360列の2次元配列になる
distances[x][y] = (distance / maxDistance) * 255;
}
}なお、キャンバスセンターとキャンバスの全ピクセルの座標を結ぶ線は、次のように表すことができます(全ピクセルまで白い線を引くと、結果としてキャンバスは全面が白くなるので、下図では10ピクセルごとに引いています)。見方を変えると、この線が長いほどその線の先端の点は白くなり、短いほど黒くなると考えることもできます。

キャンバスセンターとキャンバスのピクセルを結ぶ線からは放射状の模様が作成できます。模様は、変数spacerに代入する数値を変えることで、さまざまに変えることができます。
// spacerに割り当てる数値を変える
spacer = 20;
function draw() {
background(0);
stroke(255);
for (let x = 0; x < width; x += spacer) {
for (let y = 0; y < height; y += spacer) {
line(width / 2, height / 2, x, y);
}
}
}下図はその例です。

オブジェクトの配列
カスタムオブジェクトの配列を作成するシンタックスを例で示します。
// Moduleクラス
class Module {
// コンストラクタ関数
constructor(xOff, yOff, x, y, speed, unit) {
this.xOff = xOff;
this.yOff = yOff;
this.x = x;
this.y = y;
this.speed = speed;
this.unit = unit;
this.xDir = 1;
this.yDir = 1;
}
// 変数を更新するカスタムメソッド
update() {
this.x = this.x + this.speed * this.xDir;
if (this.x >= this.unit || this.x <= 0) {
this.xDir *= -1;
this.x = this.x + 1 * this.xDir;
this.y = this.y + 1 * this.yDir;
}
if (this.y >= this.unit || this.y <= 0) {
this.yDir *= -1;
this.y = this.y + 1 * this.yDir;
}
}
// このオブジェクトを描画するカスタムメソッド
draw() {
fill(255);
ellipse(this.xOff + this.x, this.yOff + this.y, 6, 6);
}
}
// Moduleクラス定義ここまで
let unit = 40;
let count;
let mods = [];
function setup() {
createCanvas(720, 360);
noStroke();
let wideCount = width / unit;
let highCount = height / unit;
count = wideCount * highCount;
let index = 0;
for (let y = 0; y < highCount; y++) {
for (let x = 0; x < wideCount; x++) {
mods[index++] = new Module(
x * unit,
y * unit,
unit / 2,
unit / 2,
random(0.05, 0.8),
unit
);
}
}
}
function draw() {
background(0);
for (let i = 0; i < count; i++) {
mods[i].update();
mods[i].draw();
}
}解説
オブジェクトの配列とは、要素としてオブジェクトを持った配列を言います。上記サンプルの場合、オブジェクトはModuleオブジェクトで、modsという名前の配列に入れて管理しています。
上記サンプルはまた、JavaScriptのクラスと呼ばれる方法でオブジェクトを作成する、オブジェクト指向プログラミングの例でもあります。この手法は、同じようなたくさんのものを同じように動かしたい場合に役立ちます。
上記サンプルでは、1つのJavaScriptファイル(sketch.js)にクラスを定義するコードと、通常のp5.js関数(setup()やdraw()など)が記述されていますが、クラスを定義するコードを別に設けることもできます。
以降では、クラスをメインのコードと分けて記述する方法を見ていきます。また、上記サンプルでは、初見では理解しづらい難しい書き方がされている箇所もあるので、そういった部分も複数にばらして見ていきます。
Moduleクラスのコード
上記サンプルのModuleクラスのコード(class Module { から } // Moduleクラス定義ここまで)は、Moduleクラスを定義するJavaScriptファイルとして、メインのコードとは別に配置できます。以降では、index.html(とsketch.js)ファイルのあるフォルダにjsフォルダを作成し、その中にModule.jsという名前で保存します(クラスを定義したファイルは慣習としてクラス名を使って大文字で始められます)。
js/Module.js
class Module {
constructor(xOff, yOff, x, y, speed, unit) {
// オフセット量 => キャンバスの(0, 0)からどれだけずらして配置するか
// => キャンバスの右、下のオブジェクトほどこの量は大きくなる
this.xOff = xOff;
this.yOff = yOff;
// 自分の位置
this.x = x;
this.y = y;
// 自分のスピード
this.speed = speed;
// 自分の占有範囲、縄張り
this.unit = unit;
// 自分の進む向き
this.xDir = 1;
this.yDir = 1;
//
this.color = color(random(255, 0), random(255, 0), random(255, 0));
}
// 変数を更新するカスタムメソッド
update() {
// 自分の位置を更新(毎フレーム、スピード分だけ、右か左に移動する)
this.x = this.x + this.speed * this.xDir;
// 自分の縄張りを超えたら反転
if (this.x >= this.unit || this.x <= 0) {
// 右なら左、左なら右に向きを変える
this.xDir *= -1;
// 位置を微調整
this.x = this.x + 1 * this.xDir;
this.y = this.y + 1 * this.yDir;
}
if (this.y >= this.unit || this.y <= 0) {
this.yDir *= -1;
this.y = this.y + 1 * this.yDir;
}
}
// このオブジェクトを描画するカスタムメソッド
draw() {
// 塗りは白
fill(this.color);
// 自分のオフセット量にその時点での自分の位置を中心に、半径6の円を描く
ellipse(this.xOff + this.x, this.yOff + this.y, 6, 6);
}
}Module.jsファイルはindex.htmlの<head>タグ内で、ほかのライブラリなどと同じ要領で読み込みます。
index.html
<script src="https://cdnjs.cloudflare.com/ajax/libs/p5.js/0.8.0/p5.min.js"></script>
<!-- Module.jsを読み込む -->
<script src="js/Module.js"></script>
</head>
<body>
<script src="sketch.js"></script>
</body>class Module { の次の行にあるconstructor(xOff, yOff, x, y, speed, unit) { は、コンストラクタと呼ばれる関数で、Moduleオブジェクトのインスタンスが作成されるときに1回だけ呼び出されます。カッコ内のxOffやyOff, x, y, speed, unitはコンストラクタに渡されるパラメータで、そのインスタンスの特徴の決定に使用されます。
その後のthis.xOff = xOff; 以降は、インスタンスの作成時に渡されたパラメータをそのインスタンスのプロパティとして設定するコードです。たとえばthis.color = color(random(255, 0), random(255, 0), random(255, 0));では、random()関数によってインスタンスごとに決まる色が異なることになるので、そのインスタンスを特徴づける固有の色になります。キーワードthisはそのインスタンスを指し示すために使用します。
その後はインスタンスで使用できる関数(メソッド)を定義しています。update()はそのインスタンスの位置を更新し、draw()はそのインスタンスを描画します。draw()はp5.jsのdraw()と名前が同じですが、これはModuleクラスのメソッドであり、Moduleクラスのインスタンスでないと呼び出せません。
sketch.jsは次のように記述します。
sketch.js
const unit = 40;
let count;
let mods = [];
function setup() {
createCanvas(720, 360);
noStroke();
const wideCount = width / unit; // 720 / 40 = 18 => 水平方向の個数
const highCount = height / unit; // 360 / 40 = 9 => 垂直方向の個数
count = wideCount * highCount; // 18 * 4 = 72 => 総数
let index = 0; // mods配列のインデックス番号を参照する変数
// yを0から9未満まで、1ずつ大きくする
for (let y = 0; y < highCount; y++) {
// xを0から18未満まで、1ずつ大きくする
for (let x = 0; x < wideCount; x++) {
// Moduleオブジェクトを作成する。
// new Module( xOff, yOff, x, y, speed, unit)
const mod = new Module(
x * unit,
y * unit,
unit / 2,
unit / 2,
random(0.05, 0.8),
unit
);
// mods配列のindex番めにModuleオブジェクトを割り当てる
mods[index] = mod;
// 変数indexを1大きくする
index++;
}
}
// print(mods.length); // 162
// print(count); // 162
}
function draw() {
background(0);
// Moduleオブジェクトの数分だけ、mods配列内のModuleオブジェクトの
// update()とdraw()メソッドを呼び出す
for (let i = 0; i < count; i++) {
mods[i].update();
mods[i].draw();
}
}Moduleクラスのインスタンスを作成しているのは、setup()関数のforループにある次のコードです。
const mod = new Module(
x * unit,
y * unit,
unit / 2,
unit / 2,
random(0.05, 0.8),
unit
);クラスのインスタンスは、new クラス名()を呼び出すことでクラスに定義したコンストラクタが呼び出され、作成されます。ここでは、Moduleクラスのコンストラクタで定義したxOff, yOff, x, y, speed, unitパラメータとして、 x * unit, y * unit, unit / 2, unit / 2, random(0.05, 0.8), unit を渡しています。インスタンスは作成されると返されるので、変数modが参照することになります。
いささか感覚的すぎる言い方ですが、インスタンスの作成は、コンピュータのメモリの中に新しい生命を誕生させるようなものです。それまでは存在しなかったものが、メモリの中に確かに存在するようになり、自分の位置や方向、色などを持って動き出すのです。
mod配列へのインスタンスの割り当ては次のコードで行っています。
// mods配列のindex番めにModuleオブジェクトを割り当てる
mods[index] = mod;
// 変数indexを1大きくする
index++;インスタンスのメソッドを呼び出すには、そのインスタンスへの参照に.(ドット)とメソッドをつなげて呼び出します。上記の例ではインスタンスは全部mods配列の要素として参照しているので、次のforループから呼び出すことができます。
// Moduleオブジェクトの数分だけ、mods配列内のModuleオブジェクトの
// update()とdraw()メソッドを呼び出す
for (let i = 0; i < count; i++) {
mods[i].update();
mods[i].draw();
}