５：制御(Control)

繰り返し

for構造を使った繰り返し。同じ形状を反復する図形の描画に利用できます。次の例では、分かりやすいように、p5.jsのサンプルコードを少し書き換えています。

// このプログラムを通して、 矩形の開始位置として
// 何度も上書きして使用するグローバル変数
let y;
// これは固定的なグローバル変数
const num = 14;

function setup() {
    createCanvas(720, 360);
    background(102);
    noStroke();

    // 白い横棒を５本、縦に並べて描く
    fill(255); // 塗りを白に
    // yを60に設定
    y = 60;
    printY();

    // iを0から14/3未満(=4)まで、1ずつ大きくする => iは0,1,2,3,4と変化する
    for (let i = 0; i < num / 3; i++) {
        print('1つめのforループ');
        printY();
        // rect(x, y, w, h)
        // yは20ずつ大きくなるので、描かれる矩形の左上隅は20ずつ下がる
        rect(50, y, 475, 10);
        // 繰り返しのたびにyを20大きくする
        y += 20;
    }

    // 赤い矩形描く
    fill(255, 0, 0); // 赤
    y = 40;
    printY();
    // 左の矩形を14本、縦に並べて描く
    for (let i = 0; i < num; i++) {
        print('2つめのforループ');
        printY();
        rect(405, y, 30, 10);
        y += 20;
    }

    y = 50;
    printY();
    // その右下に、少しずらして赤い矩形を14本、縦に並べて描く
    // このずらし方で、複雑な形状になる
    for (let i = 0; i < num; i++) {
        print('3つめのforループ');
        printY();
        rect(425, y, 30, 10);
        y += 20;
    }

    // 薄青の細い矩形を描く
    y = 45;
    printY();
    fill(0, 200, 200);
    // iを0からnum-1未満(13)まで、1ずつ大きくする
    for (let i = 0; i < num - 1; i++) {
        rect(120, y, 40, 2);
        print('4つめのforループ');
        printY();
        y += 20;
    }
}

function printY() {
    print('yは今 : ' + y);
}

上記コードをブラウザで開くと、下図の結果が得られます。

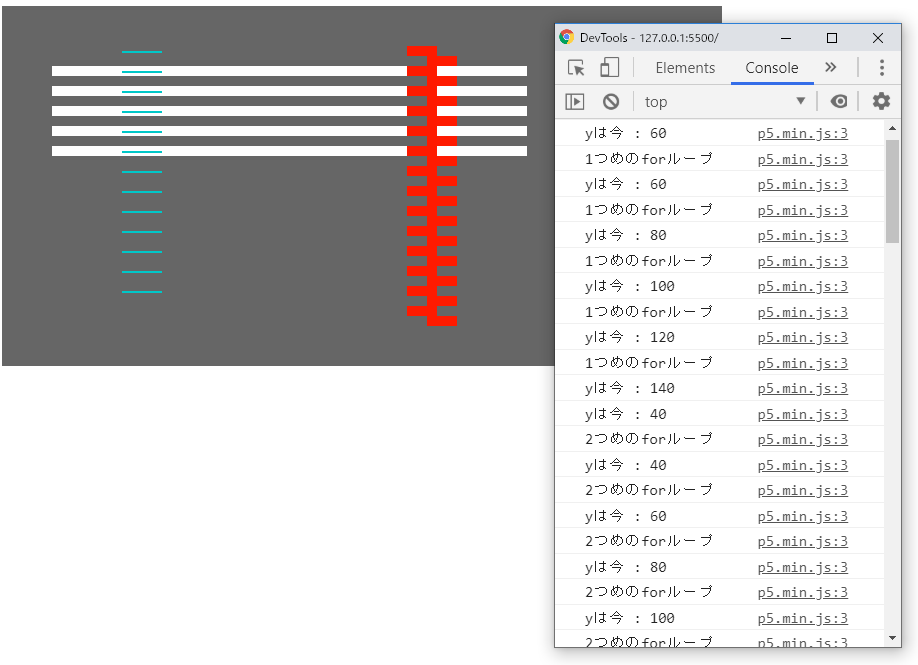
解説

ここでは、繰り返しのforループを４つ使い、そのたびに変数yの値を調整して幅と高さの異なる矩形を描画し、結果として少し複雑に見える”模様”を表現しています。

変数yはコードの冒頭で宣言されており、このプログラム(sketch.js)のどこからでも見ることのできるグローバルな変数として、forループの内外で何度も値が再代入されています。これは、「3：データ(Data)」の「変数」で見た使い方ですが、あくまでも変数の働きを示すための例だろうと思われます。

変数yは値が何度も上書きされ、ある時点での値が実際にいくつなのか分かりづらくなっています。このサンプルのような何らかの模様を描くことが目的の場合には、各部分に専用の変数をローカルで設定するのが適切だろうと思われます。変数yの値がどのように変化していくかは、コードのいくつかの箇所に仕込んだprint()関数の出力結果で確認できます。

forループでは同様の処理を何回も繰り返すことができるので、このサンプルのように、矩形の描画位置を少しずつずらすことで、形状の並びを一気に作成することができます。forループの働きが難しく思えるときには、変化する変数を実際の値に置き換えて、繰り返しを１つずつ追ってみると、理解しやすくなります。

for (let i = 0; i < num / 3; i++) {
    rect(50, y, 475, 10);
    y += 20;
}

このforループは、0からスタートしたiが14/3未満つまり4になるまで、iを1ずつ大きくします。したがってiは0,1,2,3,4と変化し、ループは5回繰り返されます。

1回めの繰り返しでは、yは60なので、rect(50, 60, 475, 10)となり、(50, 60)から475×10の矩形が描かれます。その後yは80になります。2回めの繰り返しでは、yは80なので、rect(50, 80, 475, 10)となり、(50, 80)から475×10の矩形が描かれます(つまり矩形は下にずれて描画される)。その後yは100になります。以降も同様です。

２つめと３つめのループで描いている赤い矩形から結果として表現される模様は少し複雑ですが、その仕掛けはいたって単純で、３つめのループで描く矩形の開始位置を、下に10、右に20移しているだけです。

繰り返しの埋め込み(二重ループ)

for構造を埋め込むことで２次元での繰り返しが可能になります。

function setup() {
    createCanvas(720, 360);
    background(0);
    noStroke();

    let gridSize = 35;

    //let num = 0;

    // xを35から開始し、720-35=685以上になるまで、35ずつ大きくする
    for (let x = gridSize; x <= width - gridSize; x += gridSize) {
        // yを35から開始し、360-35=325以上になるまで、35ずつ大きくする
        for (let y = gridSize; y <= height - gridSize; y += gridSize) {
            print('x : ' + x, 'y : ' + y);

            noStroke();
            fill(255);

            // text(num, x, y);
            // num++;

            // 小さな白い正方形を(x-1,y-1)に描画
            rect(x - 1, y - 1, 3, 3);
            // 線を半透明の黄にする
            stroke(255, 255, 0, 50);
            // (x,y)とキャンバスのセンターを結ぶ線を描画
            line(x, y, width / 2, height / 2);

        }
    }
}

上記コードからは次の結果が表示されます。コンソールに出力されるxとy値も合わせて確認してください。

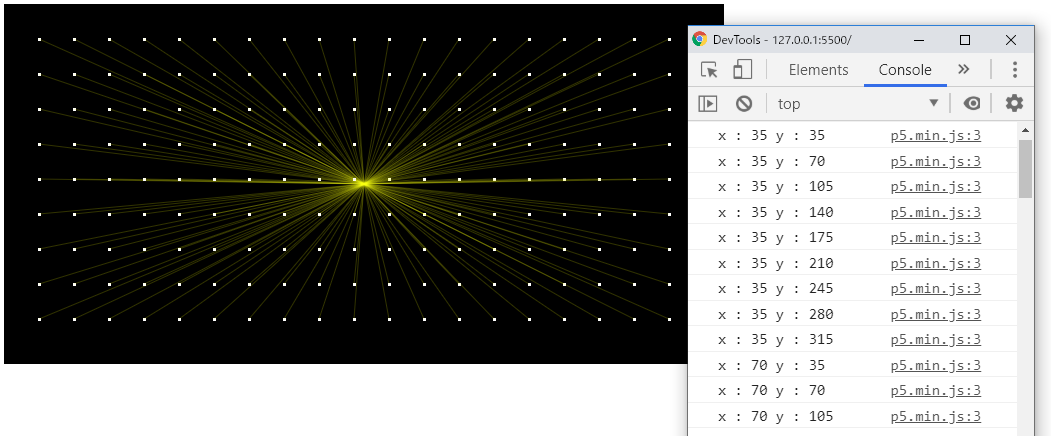
解説

２次元と聞くと難しく思えるかもしれませんが、縦横の２方向が扱えるようになる、ということです。

上記サンプルで出力されるxとyの値を見ると、外側のforループの１回めの繰り返しでxが35のとき、内側のforループでは繰り返しが9回実行され、yは35,70,105,140,175,210,245,280,315と変化します。このxとyがrect(x – 1, y – 1, 3, 3)で使われるので、3×3の正方形がキャンバス左端に縦に９個並ぶことになります。

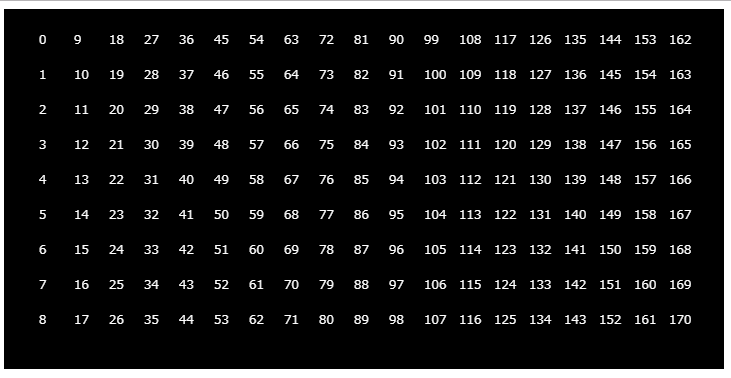
正方形がどういう順番で描画されているかは、矩形を描く代わりに順番を表す数字を描画すると確認しやすくなります(上記サンプルで//をつけているコード行)。

条件１

条件は質問のようなものです。条件を使用することで、質問に対する答えが真の場合にあるアクションを取り、答えが偽の場合には別のアクションを取ることが可能になります。プログラム内の質問はつねに論理的か相関的なステートメントです。たとえば変数iが0に等しいなら、線を描画します。

function setup() {
    createCanvas(720, 360);
    background(0);
    // iを10から開始し、720未満まで、10ずつ大きくする
    for (let i = 10; i < width; i += 10) {
        print(i); // 10,20,30,...,700,710

        // iが20で割り切れる場合には(余りが0)、短い白線を描画し、
        // そうでない場合には、長い赤線を描画する
        // iは10ずつ大きくなるので、白線と赤線は交互に引かれることになる。
        if (i % 20 === 0) {
            print('20で割り切れる');
            stroke(255);
            line(i, 80, i, height / 2);
        }
        else {
            print('20で割り切れない');
            stroke(255, 0, 0);
            line(i, 20, i, 180);
        }
    }
}

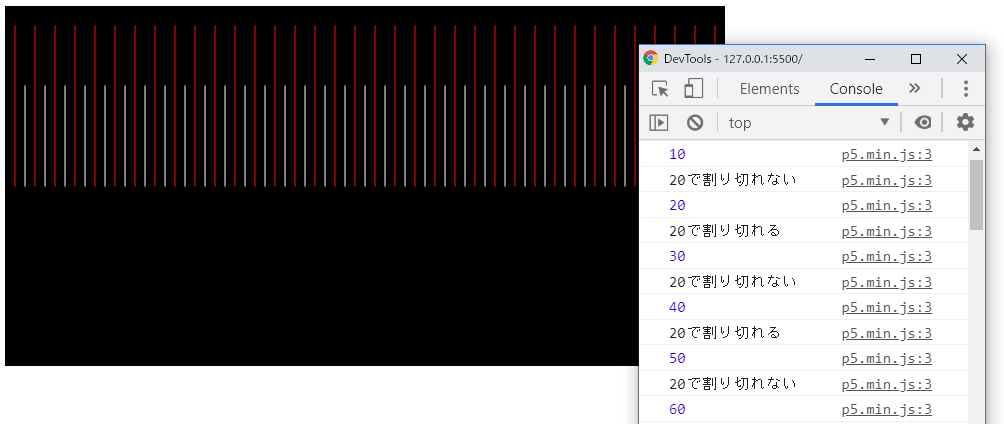
解説

上記サンプルでは、forループの変数iは10から710まで10ずつ大きくなります。その中のifステートメントでは、i % 20 === 0、つまりiが20で割り切れるかどうかを調べているので、条件に当てはまる場合とそうでない場合が交互に来ることになります。

この規則性を利用すると、たとえば次のような星型と円を交互に描画するプログラムが簡単に作成できます。星型の作成については「２：形(Form)」で述べています。

条件２

キーワードelseを追加することで、前のサンプルの条件の言語が拡張できます。これにより、それぞれが異なるアクションを持った、２つ以上の連続する質問を行う条件が可能になります。

function setup() {
    createCanvas(720, 360);
    background(0);

    // iを2から開始し、720-2(=718)未満まで、7ずつ大きくする
    for (let i = 2; i < width - 2; i += 7) {
        print('iは今 : ' + i);
        // iが20で割り切れる場合には(余りが0)、白線を描く
        if (i % 20 === 0) {
            print('20で割り切れる');
            stroke(255);
            line(i, 80, i, height / 2);
            // そうでなく、iが10で割り切れる場合には、赤線を描く
        }
        else if (i % 11 === 0) {
            print('10で割り切れる');
            stroke(255, 0, 0);
            line(i, 20, i, 180);
            // 上の２つの条件がどれも満たされない場合には、黄線を描く
        }
        else {
            // print('20でも10でも割り切れない');
            stroke(255, 255, 0);
            line(i, height / 2, i, height - 20);
        }
    }
}

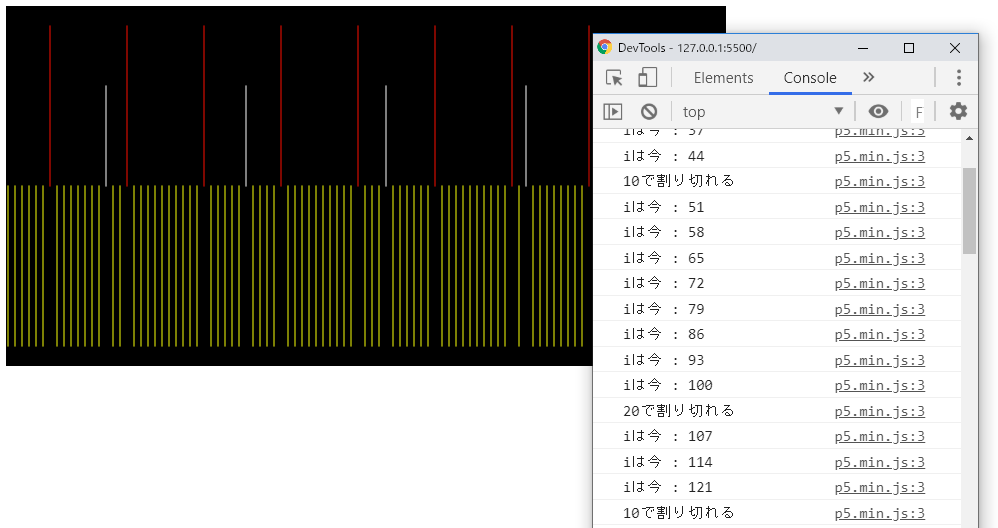
解説

このサンプルでは、forループの変数iの増分(7など)や、ifステートメントの条件(i % 20 === 0やi % 11 === 0)を変えることで、結果として描かれる線の模様が変わります。数値の選定には数学的なセンスが求められますが、うまくはまれば幾何学的な美しい模様が作成できます。これは、p5.jsの面白い特徴でもあります。

論理演算子

論理演算子を表す&&(論理積、AND、かつ)と||(論理和、OR、または)は、単純な相関的ステートメントをより複雑な式に結合するために使用されます。|(否定、NOT、でない)はブールステートメントの否定に使用されます。

let test = false;

function setup() {
    createCanvas(720, 360);
    background(126);

    // iを5から開始し、360以下まで、5ずつ大きくする
    for (let i = 5; i <= height; i += 5) {
        print(i); // 5,10,15,...,355,360
        // 論理積(AND)
        // iが35より大きくかつ100未満なら、赤線を描く
        if (i > 35 && i < 100) {
            stroke(255, 0, 0);
            line(width / 4, i, width / 2, i);
            test = false;
        }

        // 論理和(OR)
        // iが35以下かまたは100より大きいなら、
        if (i <= 35 || i >= 100) {
            stroke(255, 255, 0);
            line(width / 2, i, width, i);
            test = true;
        }

        print(test);

        // ブール値がtrueであるかどうかをテスト
        // 式if(test)はif(test==true)と同じ
        if (test) {
            // 黒の縦向きの点線
            stroke(0);
            point(width / 3, i);
        }

        // ブール値がfalseであるかどうかをテスト
        // 式if(!test)はif(test==false)と同じ
        if (!test) {
            // 白の縦向きの点線
            stroke(255);
            point(width / 4, i);
        }
    }
}

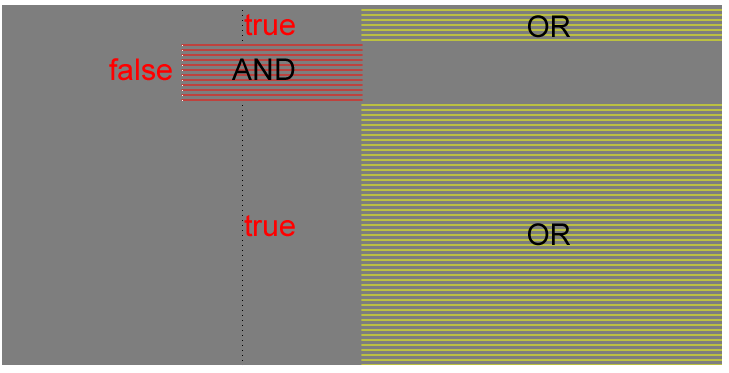
解説

論理演算は集合のベン図で考えると理解しやすくなります。

function setup() {
    createCanvas(720, 360);
    background(126);
    noStroke();

    const radius = 100
    fill(255, 255, 0);
    ellipse(width / 2, height / 2, radius * 2 + 20);

    // キャンバス全体を(10,10)から右下隅まで、20ずつ走査
    for (let x = 10; x < width; x += 20) {
        for (let y = 10; y < height; y += 20) {
            // (x,y)とキャンバスセンターとの距離
            let distance = dist(x, y, width / 2, height / 2);
            // radius+20より離れているなら
            if (distance > radius + 20) {
                // グレーの円を描く
                fill(150);
                ellipse(x, y, 10);
                // そうでなければ
            }
            else {
                // 赤いの星型を描く
                fill(255, 0, 0);
                star(x, y, 8, 4, 5)
            }
        }

    }
}

function star(x, y, radius1, radius2, npoints) {
    let angle = TWO_PI / npoints;
    let halfAngle = angle / 2.0;
    beginShape();
    for (let a = 0; a < TWO_PI; a += angle) {
        let sx = x + cos(a) * radius2;
        let sy = y + sin(a) * radius2;
        vertex(sx, sy);
        sx = x + cos(a + halfAngle) * radius1;
        sy = y + sin(a + halfAngle) * radius1;
        vertex(sx, sy);
    }
    endShape(CLOSE);
}