p5.jsサンプルの「Simulate」項の解説として、このページでは、「力」、「パーティクルシステム」、「群れ行動」、「ウルフラム セル・オートマトン」、「ライフゲーム」、「複数のパーティクルシステム」、「スピログラフ」、「L-system」、「ばね」、「複数のばね」サンプルを解説しています。
目次
力
剛体(変形しない物体)に作用する複数の力のシミュレーション(natureofcode.com)
sketch.js
// 変形しない剛体(Moverクラス)に作用する複数の力のデモ
// 剛体は、始終、重力の影響を受ける
// 剛体は、水中にいるとき、流体抵抗の影響を受ける。
// Moverオブジェクトを入れて管理する配列
let movers = [];
// Liquidオブジェクト
let liquid;
function setup() {
createCanvas(640, 360);
reset();
// Liquidオブジェクトを作成
liquid = new Liquid(0, height / 2, width, height / 2, 0.1);
}
function draw() {
background(127);
// Liquidオブジェクトを描く
liquid.display();
// MoverオブジェクトがLiquidオブジェクトの範囲内にいるかどうかを調べ、いるなら流体抗力を適用する
// その後、重力を適用する
for (let i = 0; i < movers.length; i++) {
// Moverオブジェクトが水中にいるのなら
if (liquid.contains(movers[i])) {
// 流体抗力を計算
let dragForce = liquid.calculateDrag(movers[i]);
// 流体抗力をMoverオブジェクトに適用
movers[i].applyForce(dragForce);
}
// 質量にかかる重力はここで求める。
// 0.1はこのシミュレーションに適した値として選ばれた数値
let gravity = createVector(0, 0.1 * movers[i].mass);
// 重力を適用
movers[i].applyForce(gravity);
// 更新と表示
movers[i].update();
movers[i].display();
movers[i].checkEdges();
}
}
// マウスプレスでリセット
function mousePressed() {
reset();
}
// すべてのMoverオブジェクトをランダムに再スタート
// この関数はsetup()とmousePressed()で呼び出される
function reset() {
// Moverオブジェクトの数は9個
for (let i = 0; i < 9; i++) {
movers[i] = new Mover(random(0.5, 3), 40 + i * 70, 0);
}
}Mover.js
// Moverクラス
class Mover {
constructor(m, x, y) {
this.mass = m; // 質量(0.5->3のランダムな値)
this.position = createVector(x, y); // 位置(x, y) = (40 + i * 70, 0)
this.velocity = createVector(0, 0); // スピード(最初は0)
this.acceleration = createVector(0, 0); // 加速度(最初は0)
this.radius = this.mass * 8; // 半径 質量の大きいものほど大きくする
}
// ニュートンの第二法則 加速度の大きさは,力の大きさに比例し,質量に反比例する。
// 力の大きさと加速度,質量の関係
// 力の大きさ = 質量 * 加速度 => 加速度 = 力の大きさ / 質量
// http://w3e.kanazawa-it.ac.jp/math/physics/high-school_index/mechanics/force/henkan-tex.cgi?target=/math/physics/high-school_index/mechanics/force/second_law_of_motion.html
applyForce(force) {
// 力を質量で割って加速度を求める
// div() ベクトルをスカラーで割る
const f = p5.Vector.div(force, this.mass); // p5.Vector.divは静的メソッド
// 加速度をaccelerationプロパティに加算する
this.acceleration.add(f);
}
update() {
// スピードは加速度に応じて変化する
this.velocity.add(this.acceleration);
// 位置はスピードによって変化する
this.position.add(this.velocity);
// 加速度は毎フレーム、クリアする必要がある。
// mult() ベクトルにスカラーを掛ける
this.acceleration.mult(0);
}
display() {
stroke(0);
strokeWeight(2);
fill(255, 127);
// 円を描画。質量が大きいほどサイズも大きい
ellipse(this.position.x, this.position.y, this.radius * 2);
}
// キャンバス下端で跳ね返る
checkEdges() {
if (this.position.y > (height - this.radius)) {
// スピードは下端に当たると落ちる
this.velocity.y *= -0.9;
// y位置を固定しないと、跳ね返り後、円が下端に少しめり込んで見える
this.position.y = (height - this.radius);
}
}
}Liquid.js
// Liquidクラス
class Liquid {
constructor(x, y, w, h, c) {
this.x = x; // x位置 = 0
this.y = y; // y位置 = height / 2
this.w = w; // 幅 = width
this.h = h; // 高さ = height / 2
this.c = c; // スピードに掛ける係数 = 0.1
}
// Moverオブジェクトが水中にいるかどうか
// mはMoverオブジェクト、positionはMoverオブジェクトのプロパティ
contains(m) {
const l = m.position;
return l.x > this.x && l.x < this.x + this.w &&
l.y > this.y && l.y < this.y + this.h;
};
/*
contains(m) {
const mx = m.position.x;
const my = m.position.y;
const left = this.x;
const right = this.x + this.w;
const top = this.y;
const bottom = this.y + this.h;
// mがthisの境界内にいるかどうか
if (mx > left && mx < right && my > top && my < bottom) {
return true;
} else {
return false;
}
}
*/
// 流体抗力を計算して返す mはMoverオブジェクト
calculateDrag(m) {
// mad() ベクトルの大きさ(長さ)を計算する
const speed = m.velocity.mag();
// ニュートンの抵抗法則
// 流体中を物体が運動するとき、物体には抵抗が働く。物体の速度が比較的大きい場合,抵抗の大きさは速度の2乗に比例する。
// https://kotobank.jp/word/%E3%83%8B%E3%83%A5%E3%83%BC%E3%83%88%E3%83%B3%E3%81%AE%E6%8A%B5%E6%8A%97%E6%B3%95%E5%89%87-110555
const dragMagnitude = this.c * speed * speed;
// mはMoverオブジェクトの速度をコピー
const dragForce = m.velocity.copy();
// 抗力の向きはスピードの逆
dragForce.mult(-1);
// 向きの情報だけにするために、正規化する
// https://yttm-work.jp/math/math_0002.html#head_line_07
dragForce.normalize();
// 向き情報に抗力の大きさを掛ける
dragForce.mult(dragMagnitude);
return dragForce;
}
display() {
noStroke();
fill(50);
rect(this.x, this.y, this.w, this.h);
}
}画面のクリックでリスタートできます。
解説
水よりも重たい球を水中に落とし、球が水底に着くまでのシミュレーションです。物理学の法則を利用しているので、重力や流体抗力(水の抵抗)についての法則が使われています。
とは言え、重要なのは法則の理解ではありません。同様のシミュレーションサンプルはほかにいくつも公開されているので、法則を適宜当てはめればよいだけです。ここで重要なのは、p5.jsのp5.Vectorの理解です。
説明
2次元または3次元の、具体的にはユークリッド(幾何学)ベクトルと呼ばれるベクトルを表すためのクラス。ベクトルは、大きさと方向を持つ実体だが、そのデータ型はベクトルの成分(2Dではxとy、3DではX、y、z)を保持する。大きさと方向には、mag()とheading()メソッドでアクセスできる。
多くのp5.jsサンプルでは、位置や速度(スピード)、加速度を表すのにp5.Vectorが使用されている。たとえば、画面を矩形が移動する場合、矩形はどの瞬間でも、位置(原点からその場所を指し示すベクトル)と、速度(オブジェクトの位置が時間単位ごとに変化する割合、ベクトルとして表される)、加速度(オブジェクトの速度が時間単位ごとに変化する割合、ベクトルとして表される)を持っている。
ベクトルは値のまとまりを表すので、通常の加減乗除は使用できない。そのためには”ベクトル”数学”が必要になるが、p5.Vectorクラスのメソッドによって、簡単になる。
フィールド
x: ベクトルのx成分
y: ベクトルのy成分
z: ベクトルのz成分
メソッド(抜粋)
add():
x、y、z成分をベクトルに加算するか、ベクトルを別のベクトルに加算するか、または2つの別々のベクトルを加算する。2つの別々のベクトルを加算するメソッドのバージョンは静的メソッド(p5.Vector.add())で、p5.Vectorを返す。ほかの2つのメソッドはベクトルに直接作用する。
mult():
ベクトルにスカラーを掛ける。このメソッドの静的バージョンは新しい p5.Vectorを作成するが、非静的バージョンは直接ベクトルに作用する。
div():
ベクトルをスカラーで割る。このメソッドの静的バージョンは新しい p5.Vectorを作成するが、非静的バージョンは直接ベクトルに作用する。
mag():
ベクトルの大きさ(長さ)を計算して、浮動小数点数として返す(これは、ピタゴラスの定理、sqrt(xx + yy + z*z)と同じ)
normalize():
ベクトルを長さ1に正規化する(単位ベクトルにする)
heading():
このベクトルの回転角度を計算する(2Dベクトルのみ)
説明
新しいp5.Vector(ベクトルを保持するデータ型)を作成する。これにより、ユークリッド(幾何学)ベクトルと呼ばれる、2次元または3次元のベクトルが扱えるようになる。ベクトルは大きさと方向を持つ実体。
シンタックス
createVector([x], [y], [z])
p5.Vectorを使ったベクトルの簡単な復習
p5.Vectorを使って、ベクトルを簡単に復習します。
function setup() {
createCanvas(400, 400);
background(155);
const v1 = createVector(200, 300);
// v1のxとy成分を出力
print(v1.x, v1.y); // 200, 300
// v1を線で表す
line(0, 0, v1.x, v1.y);
// v1の大きさ => 斜辺の長さと同じ
print(v1.mag()); // 360.5551275463989
}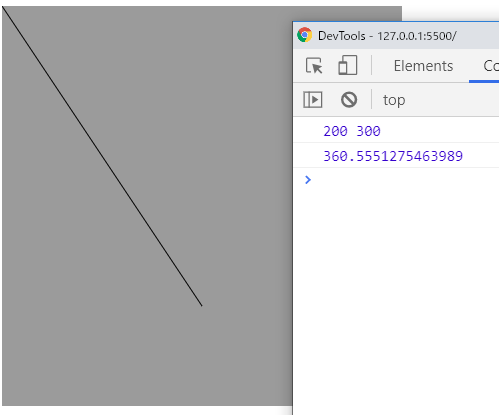
createVector(200, 300)によって、xプロパティ値に200、yプロパティ値に300を持つp5.Vectorオブジェクトv1が作成されます。これは、(0, 0)と(v1.x, v1.y)を結んだ直線で表すことができます。
p5.Vectorオブジェクトのmag()メソッドを使うと、そのベクトルの大きさが分かります(360.5551275463989)。これは、直角三角形の斜辺の長さなので、ピタゴラスの定理(c*c = a*a + b*b)で求めることと同じです。
ベクトルの足し算を見てみます。ベクトルの足し算とはベクトルの成分同士を足すことで、add()メソッドで行います。
function setup() {
createCanvas(400, 400);
background(200);
// v1を赤線で描く
const v1 = createVector(100, 25);
stroke(255, 0, 0);
line(0, 0, v1.x, v1.y);
// v2を緑線で描く
const v2 = createVector(50, 50);
stroke(0, 255, 0);
line(0, 0, v2.x, v2.y);
// v1とv2を足したv3を青線で描く
const v3 = v1.add(v2);
stroke(0, 0, 255);
line(0, 0, v3.x, v3.y);
print(v3.x, v3.y); // 150, 75 => 100+50, 25*50
}ここではベクトルv1(赤)とv2(緑)をv1のadd()メソッドで足しています。結果はベクトルv3(青)で、これは(0, 0)と(150,75)を結ぶ直線で表すことができます。v1 + v2 = (100, 25) + (50, 50) = (150, 75)という計算です。
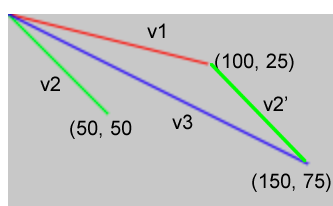
ポイントは、ベクトルは大きさと方向だけを持つもので、位置は関係しないということです。ベクトルの足し算について、学校では、足す方の矢印の先と足される方の尾を合わせ、足す方の尾と足される方の先を結ぶと、足した結果のベクトルになる、と教わりましたが、これは、上図のv2を平行移動させ尾を(100, 25)に合わせると、その先は(150, 75)に重なることでも分かります。
位置と速度と加速度
物理学の法則を適用するシミュレーションでは、速度や加速度をベクトルとしてとらえた方が、公式が適用しやすくなります。位置もそれに合わせて、ベクトルにします。
次のコードでは、位置を変数positionVectorとして、createVector(0, 0)の結果を代入しています。簡単にいうと、(0, 0)の原点をベクトルで表しているということです。velocityVectorは速度のベクトルで、線で描くと(0, 0)と(1, 1)を結んだ直線です。
let positionVector, velocityVector
function setup() {
createCanvas(400, 400);
background(155);
positionVector = createVector(0, 0);
velocityVector = createVector(1, 1);
}
function draw() {
background(155);
// 速度は位置を変更する
positionVector = positionVector.add(velocityVector);
ellipse(positionVector.x, positionVector.y, 10);
}draw()関数では、positionVector.add(velocityVector)によって、毎フレーム、positionVectorにvelocityVectorが足されます。したがって、positionVectorは最初(0, 0)だったものが、(1, 1)、(2, 2)、(3, 3)と1フレーム進むごとにx、y成分ともに1ずつ大きくなっていきます。これは、定速で移動するアニメーションです。
これに加速度を加えます。それには加速度を表すベクトルをaccelerationVectorとして、setup()内で作成します。そしてdraw()内で、速度のベクトルに加速度のベクトルを足します。これにより、円はスピードアップして移動します。
let positionVector, velocityVector, accelerationVector;
function setup() {
createCanvas(400, 400);
background(155);
positionVector = createVector(0, 0);
velocityVector = createVector(1, 1);
accelerationVector = createVector(0.1, 0.1);
}
function draw() {
background(155);
// 加速度は速度を変更する
velocityVector = velocityVector.add(accelerationVector);
// 速度は位置を変更する
positionVector = positionVector.add(velocityVector);
ellipse(positionVector.x, positionVector.y, 10);
}ここでのポイントは、速度は位置を変更し、加速度は速度を変更する、ということです。とは言え、描かれる円の立場から見れば、「7_2:速度と方向 p5.js JavaScript」と同じで、ここではただpositionVectorのxとyプロパティを通して位置を取得しているだけです。
物理で言う速度は、単位時間当たりの移動距離と方向を持っています。一般的に使われるスピードには方向の概念は含まれませんが、speedを速度と呼ぶ場合には、シミュレーションにおいては、スピードにも方向が含まれるべきです。
パーティクルシステム
基本的なパーティクルシステム(natureofcode.com)
sketch.js
// パーティクルシステム
let system;
function setup() {
createCanvas(720, 400);
system = new ParticleSystem(createVector(width / 2, 50));
}
function draw() {
background(51);
system.addParticle();
system.run();
}ParticleSystem.js
// ParticleSystemクラス
class ParticleSystem {
constructor(position) {
this.origin = position.copy(); // このシステムの位置
this.particles = []; // パーティクルを管理するための配列
};
// パーティクルを作成し、particles配列に追加する
addParticle() {
this.particles.push(new Particle(this.origin));
}
// 実行
run() {
// 作成
// 新しいものほど前面に描画
for (let i = this.particles.length - 1; i >= 0; i--) {
const p = this.particles[i];
p.run();
if (p.isDead()) {
this.particles.splice(i, 1);
}
}
}
}Particle.js
// Particleクラス
class Particle {
constructor(position) {
// 自分の加速度 => yは正(下向き)
this.acceleration = createVector(0, 0.05);
// 自分の速度 => xは正負均等だが、yは負(上方向)のみ
this.velocity = createVector(random(-1, 1), random(-1, 0));
//this.velocity = createVector(random(-1, 1), random(-5, 0));
this.position = position.copy(); // 自分の位置
this.lifespan = 255; // 自分の寿命
}
// 位置を更新して表示
run() {
this.update();
this.display();
}
// 位置を更新する
update() {
// 加速度は速度を変更する
this.velocity.add(this.acceleration);
// 速度は位置を変更する
this.position.add(this.velocity);
// 更新のたびに寿命が短くなる
this.lifespan -= 2;
}
// 表示する
display() {
// lifespanは次第に小さくなるので、線のグレーは薄くなる
stroke(200, this.lifespan);
strokeWeight(2);
// lifespanは次第に小さくなるので、塗り色のグレーも薄くなる
fill(127, this.lifespan);
// 自分の位置に円を描画
ellipse(this.position.x, this.position.y, 12, 12);
}
// まだ生きているか
isDead() {
return this.lifespan < 0;
}
}解説
パーティクル(particle)とは粒子、小片のことで、コンピュータグラフィックで言うパーティクルシステムは、粒子を運動させ、炎や火花、爆発、煙、流水などの様子を表現するためのシステムを言います。
ウィキペディアの「パーティクルシステム」ページにある「典型的な実装」には、次のように書かれています。
一般的に、3次元空間におけるパーティクル・システムの位置と動作はエミッター(英: emitter、放出器)と呼ばれるものによって制御される。エミッターはパーティクルの発生源として働き、3次元空間におけるエミッターの位置は、パーティクルがどこで発生しどこへ向かってゆくかを決定する。立方体や平面といった通常の立体メッシュオブジェクトをエミッターとして使うことができる。 エミッターには、パーティクルの一連の動作パラメタが設定される。設定できるパラメタの例としては、
- 発生頻度 – 単位時間あたり何個のパーティクルを生成するか
- パーティクルの初速ベクトル – 生成時の放出方向
- パーティクルの寿命 – 各パーティクルが表示されてから消滅するまでの時間間隔
- パーティクルの色、その他いろいろ
がある。
このサンプルの場合、パーティクルはキャンバスセンターの上から出てくる白い円で、同じ場所(エミッター、吹き出し口)から右に左にあふれ出て、下に落ちていき、やがて見えなくなります。
パーティクルはParticleクラス(Particle.js)で定義されます。Particleクラスのコンストラクタ関数では、吹き出すパーティクルParticle(オブジェクト)の加速度(acceleration)と速度(velocity)がcreateVector()関数によって、ベクトルとして設定されます。パーティクルの位置(position)はconstructor()関数が受け取る引数で、実はこれもベクトルです(sketch.jsで、後述するParticleSystem()に渡され、その後Particleのコンストラクタが受け取ります)。
constructor(position) {
this.acceleration = createVector(0, 0.05);
this.velocity = createVector(random(-1, 1), random(-1, 0));
this.position = position.copy();
this.lifespan = 255;
}accelerationプロパティの設定に使用しているcreateVector(0, 0.05)は、yの正、つまり下向きに働くベクトルです。一方、velocityプロパティのcreateVector(random(-1, 1), random(-1, 0))は、xはランダムな正負、つまり左右の両方向ですが、yはランダムな負、つまり上向きのベクトルになります。加速度は速度を変更するので、パーティクルの速度のyは初めこそ負の値ですが、すぐに正の値になります。これが、上に吹き出しその後落下するパーティクルを生み出します。
lifespanプロパティはパーティクルの寿命です。update()メソッドで少しずつ確実に減っていきます。
ParticleSystemクラスは、このパーティクルを作成し、自分の配列に収めて管理します。ParticleSystemのコンストラクタ関数には、sketch.jsから呼び出され、createVector(width / 2, 50)、つまり(0, 0)から(360, 50)へのベクトルが渡されます。この変数positionはParticleSystemクラスのoriginプロパティに割り当てられ、addParticle()メソッドで、Particleクラスのコンストラクタに渡されます。
constructor(position) {
this.origin = position.copy(); // このシステムの位置
this.particles = []; // パーティクルを管理するための配列
};
// パーティクルを作成し、particles配列に追加する
addParticle() {
this.particles.push(new Particle(this.origin));
}ParticleSystemクラスのrun()メソッドは、sketch.jsのdraw()関数で、addParticle()の後呼び出されます。ここでは、自分のparticles配列に持っているParticleオブジェクトに対してそのrun()メソッドを呼び出し、寿命が尽きているなら、particles配列からはずす、という作業を行います。
for (let i = this.particles.length - 1; i >= 0; i--) {
const p = this.particles[i];
p.run();
if (p.isDead()) {
this.particles.splice(i, 1);
}
}しかし、forループの()内が見慣れないことになっています。これは、新しいパーティクルほど前面に描画するためです。試しにfor (let i = 0; i < this.particles.length; i++) { に替えてみると、下図のようになります。
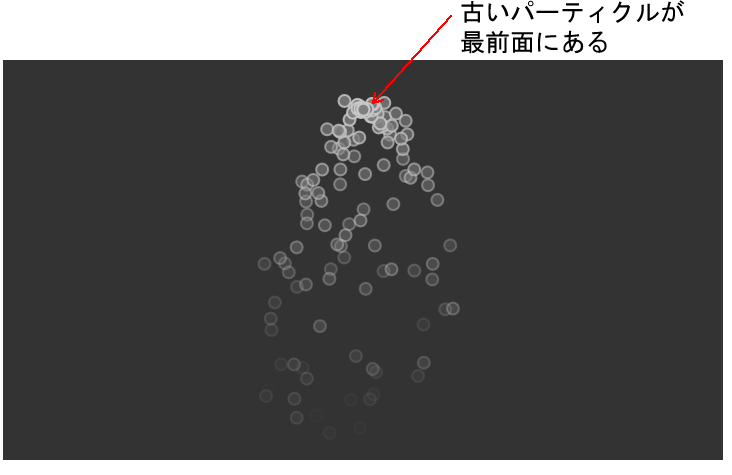
for (let i = this.particles.length – 1; i >= 0; i–) { は、particles配列を後ろの要素から扱うための方法で、これは配列のreverse()に替えることもできます。
// Array.reverse()で配列要素を逆に並びにする
const reversed = this.particles.reverse();
//古いものが最前面に描画される
for (let i = 0; i < reversed.length; i++) {
const p = reversed[i];
p.run();
if (p.isDead()) {
reversed.splice(i, 1)
}
}
// 並びを元に戻す
this.particles = reversed.reverse();このパーティクルシステムは、吹き出し口の位置をsketch.jsから指定できます。Particle.jsのvelocityプロパティをcreateVector(random(-1, 1), random(-5, 0)に変更し、吹き出し口をキャンバスセンターに設定すると、噴水のようなパーティクルになります。

群れ行動(フロッキング)
クレイグ レイノルズの”群れ行動”のデモ。https://www.red3d.com/cwr/を参照。ルール:凝集、分離、整列(https://natureofcode.comより)。マウスのドラッグでBoids(ボイド、鳥もどき)をシステムに追加できます。
sketch.js
// 群れ
let flock;
function setup() {
createCanvas(640, 360);
createP("マウスをドラッグすると、新しいボイドが生成できる");
flock = new Flock();
// 最初のボイドのセットをシステムに追加する
for (let i = 0; i < 100; i++) {
let b = new Boid(width / 2, height / 2);
flock.addBoid(b);
}
}
function draw() {
background(51);
flock.run();
}
// 新しいボイドをシステムに追加する
function mouseDragged() {
flock.addBoid(new Boid(mouseX, mouseY));
}Flock.js
// The Nature of Code
// Daniel Shiffman
// http://natureofcode.com
// Flockクラス
// 行うことは少なく、ただすべてのボイドの配列を管理するだけ
class Flock {
constructor() {
// すべてのボイド用の配列
this.boids = []; // 配列を初期化
}
run() {
for (let i = 0; i < this.boids.length; i++) {
// 個々のボイドにに、ボイドのリストを丸ごと渡す
this.boids[i].run(this.boids);
}
}
addBoid(b) {
this.boids.push(b);
}
}Boid.js
// The Nature of Code
// Daniel Shiffman
// http://natureofcode.com
// Boidクラス
// 結合、分離、整列を行うためのメソッドを持つ
class Boid {
constructor(x, y) {
// 加速度
this.acceleration = createVector(0, 0);
// 速度
this.velocity = createVector(random(-1, 1), random(-1, 1));
// 位置
this.position = createVector(x, y);
// ボイドのサイズ
this.r = 3.0;
// 最大速度
this.maxspeed = 3;
// 最大操舵力
this.maxforce = 0.05;
}
run(boids) {
this.flock(boids);
this.update();
this.borders();
this.render();
}
applyForce(force) {
// ニュートンの第二法則 力の大きさ = 質量 * 加速度 => 加速度 = 力の大きさ / 質量
// A = F / M が欲しい場合は、ここに質量が追加できる
this.acceleration.add(force);
}
// 毎回、3つのルールにもとづいて、新しい加速度を蓄積する
flock(boids) {
let sep = this.separate(boids); // 分離
let ali = this.align(boids); // 整列
let coh = this.cohesion(boids); // 結合
// これらの力に対し、任意の重み付けをする
sep.mult(1.5);
ali.mult(1.0);
coh.mult(1.0);
// 加速度に力のベクトルを追加する
this.applyForce(sep);
this.applyForce(ali);
this.applyForce(coh);
}
// 位置を更新する
update() {
// 加速度は速度を変更する
this.velocity.add(this.acceleration);
// 速度を制限
this.velocity.limit(this.maxspeed);
// 速度は位置を変更する
this.position.add(this.velocity);
// 毎回、加速度を0にリセットする
this.acceleration.mult(0);
}
// ターゲットに向かう操舵力を計算し適用する
seek(target) {
// 現在位置からターゲットを指すベクトルdesired
let desired = p5.Vector.sub(target, this.position);
// desiredを正規化し、最大速度にスケーリングする
desired.normalize();
desired.mult(this.maxspeed);
// Steering = Desired - Velocity
let steer = p5.Vector.sub(desired, this.velocity);
// 最大操舵力に制限する
steer.limit(this.maxforce);
return steer;
}
// 描画
render() {
// 速度の方向に回転させた三角形を描画する
let theta = this.velocity.heading() + radians(90);
fill(127);
stroke(200);
push();
translate(this.position.x, this.position.y);
rotate(theta);
beginShape();
vertex(0, -this.r * 2);
vertex(-this.r, this.r * 2);
vertex(this.r, this.r * 2);
endShape(CLOSE);
pop();
}
// ラッピング処理(端を超えたら逆の端から出てくる)
borders() {
if (this.position.x < -this.r) this.position.x = width + this.r;
if (this.position.y < -this.r) this.position.y = height + this.r;
if (this.position.x > width + this.r) this.position.x = -this.r;
if (this.position.y > height + this.r) this.position.y = -this.r;
}
// 分離
// 近くにいるボイドを調べ、近すぎる場合には離れる方向に向かうベクトルを返す
separate(boids) {
let desiredseparation = 25.0;
let steer = createVector(0, 0);
let count = 0;
// システム内の全ボイドについて、近すぎないかどうか調べる
for (let i = 0; i < boids.length; i++) {
let d = p5.Vector.dist(this.position, boids[i].position);
// もし距離(d)が0より大きくかつ任意の量よりも大きいなら(0は自分のとき)
if ((d > 0) && (d < desiredseparation)) {
// その近いボイドから離れるベクトルを計算する
let diff = p5.Vector.sub(this.position, boids[i].position);
diff.normalize();
diff.div(d); // 距離による重み付け
steer.add(diff);
count++; // 数をメモしておく
}
}
// 平均する -- countで割る
if (count > 0) {
steer.div(count);
}
// ベクトルが0より大きい限り
if (steer.mag() > 0) {
// レイノルズの Steering = Desired - Velocity を実装
steer.normalize();
steer.mult(this.maxspeed);
steer.sub(this.velocity);
steer.limit(this.maxforce);
}
return steer;
}
// 整列
// システム内の近くにいる全ボイドについて平均速度を計算し、その方向に向かうベクトルを返す
align(boids) {
let neighbordist = 50;
let sum = createVector(0, 0);
let count = 0;
for (let i = 0; i < boids.length; i++) {
let d = p5.Vector.dist(this.position, boids[i].position);
if ((d > 0) && (d < neighbordist)) {
sum.add(boids[i].velocity);
count++;
}
}
if (count > 0) {
sum.div(count);
sum.normalize();
sum.mult(this.maxspeed);
let steer = p5.Vector.sub(sum, this.velocity);
steer.limit(this.maxforce);
return steer;
}
else {
return createVector(0, 0);
}
}
// 結合
// 近くにいる全ボイドの平均位置(たとえばセンター)を計算し、その位置に向かうベクトルを返す
cohesion(boids) {
let neighbordist = 50;
let sum = createVector(0, 0); // 空のベクトルで開始し、これに全位置を累積する
let count = 0;
for (let i = 0; i < boids.length; i++) {
let d = p5.Vector.dist(this.position, boids[i].position);
if ((d > 0) && (d < neighbordist)) {
sum.add(boids[i].position); // 位置を追加
count++;
}
}
if (count > 0) {
sum.div(count);
return this.seek(sum); // その位置に向かう
}
else {
return createVector(0, 0);
}
}
}解説
これは、三角形の鳥もどき(ボイド)が群れを成して飛ぶ様子をシミュレーションしたサンプルです。元のプログラムは、アメリカのアニメーション・プログラマー、クレイグ レイノルズが考案したもので、それをダニエル シフマンがProcessingのプログラムとして作成し、それをp5.jsに移植したものがこのサンプルです。
「ボイド (人工生命)」ページには、
コンピュータ上の鳥オブジェクトに以下の三つの動作規則を与え、多数を同時に動かして群れの振る舞いをシミュレーションする。
- 分離(Separation)
鳥オブジェクトが他の鳥オブジェクトとぶつからないように距離をとる。- 整列(Alignment)
鳥オブジェクトが他の鳥オブジェクトと概ね同じ方向に飛ぶように速度と方向を合わせる。- 結合(Cohesion)
鳥オブジェクトが他の鳥オブジェクトが集まっている群れの中心方向へ向かうように方向を変える。結果としてこのプログラムは驚くほど自然な動きを見せ、単純な規則を用いて群体としての複雑な振る舞いを再現できることを示した。以後、改良されたアルゴリズムが映画のCGアニメーションなどに応用されている。
と書かれています。ボイドの論理的背景は、クレイグ レイノルズの「Boids」ページで読むことができます。
これをProcessingに応用したダニエル シフマンのプログラムは、著書「THE NATURE OF CODE」の6章に、自立エージェントの例の1つとして、基本的な説明ととも述べられています。「THE NATURE OF CODE」はWeb上でも読むことができます(「THE NATURE OF CODE」の「Chapter 6. Autonomous Agents」)。
上記ボイドのサンプルコードはご覧のように長く複雑です。難しそうに見えるプログラムを理解するには、その機能を1つずつ探っていくのが、遠回りに見えて、実は一番確実で、応用力もつきます。そこで以降では「Chapter 6. Autonomous Agents」を参考に、シーク(ターゲットを見つけその方向へ向かう)と分離(ほかのボイドに近い場合は離れる方向に向かう)のp5.jsでの方法について見ていくことにします。ただし、p5.Vectorの理解は必須です。
自立エージェント
「THE NATURE OF CODE」6章のタイトルにもなっているAutonomous Agentsは自立エージェントと訳されます。これは、
「何らかの環境におかれたシステムであり、その環境を感知し、自身の内的方針に従って行動する存在。内的方針とは一種の衝動である(あるいはプログラムされた目的/目標)。エージェントは環境に変化を与えるよう行動し、それによって後に感知される環境に影響を与える。」(自立エージェント)
もので、たとえばターゲットに向かう場合、誰かにその位置を教えられそこへ向かえと命令されるのではなく、自分で調べて自分からそこへ向かう、ということです。上記ボイドのサンプルでも、三角形はそのそれぞれ全部が自分で判断して行動しています。
シーク:ターゲットを見つけそこへ向かう
「Chapter 6. Autonomous Agents」の「6.3 The Steering Force」には、下図とともに次の式が書かれています。
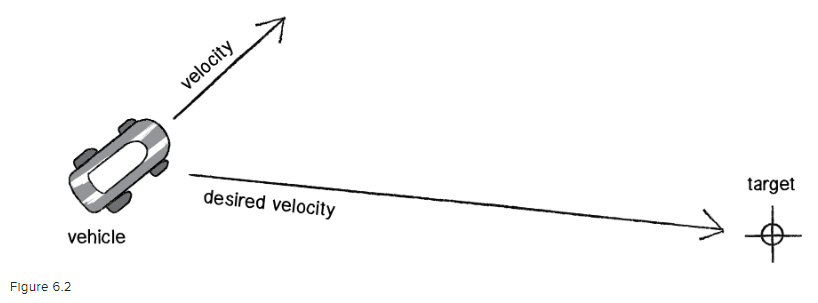
PVector desired = PVector.sub(target, location);この図は、速度velocityで移動するvehicle(乗り物)がtarget(ターゲット)に向かいたい場合、求めるベクトルdesired veloctyを示しています。式はその求め方で、ターゲットのベクトルからビークルの位置のベクトルを引きます。
次のコードは、desired veloctyを求めるp5.jsでの例です。
function setup() {
createCanvas(640, 360);
const vehiclePos = createVector(20, 250);
const vehicleVelocity = createVector(40, -40);
const targetPos = createVector(500, 300);
background(200);
// ビークルの位置のベクトルを赤線で描画
stroke(255, 0, 0);
line(0, 0, vehiclePos.x, vehiclePos.y);
// ビークルを赤丸で描画
fill(255, 0, 0);
ellipse(vehiclePos.x, vehiclePos.y, 10, 10);
// ビークルの速度のベクトルを赤線で描画(実際には見えない)
line(0, 0, vehicleVelocity.x, vehicleVelocity.y);
// ターゲットの位置のベクトルを白線で描画
stroke(255, 255, 255);
line(0, 0, targetPos.x, targetPos.y);
noStroke();
// ビークルを白丸で描画
fill(255, 255, 255);
ellipse(targetPos.x, targetPos.y, 20, 20);
// 望まれるベクトルを青線で描画
const desired = p5.Vector.sub(targetPos, vehiclePos);
stroke(0, 0, 255);
line(0, 0, desired.x, desired.y);
// ビークルをターゲットに向かわせるベクトルの計算
// ビークルの位置のベクトル + 望まれるベクトル
vehiclePos.add(desired);
// 計算後のビークルを赤丸で描画
noStroke();
fill(255, 0, 0);
ellipse(vehiclePos.x, vehiclePos.y, 10, 10);
}下図はこの実行結果です。desired veloctyを表す青線は上の方に描かれますが、ベクトルに位置は関係ないので、平行移動させると、ビークルの位置とターゲットの位置を結ぶ線になることが分かります。また最初左下にあった赤丸のビークルの位置は、vehiclePos.add(desired)によって、ターゲットの白丸と同じ位置に移ることも分かります。
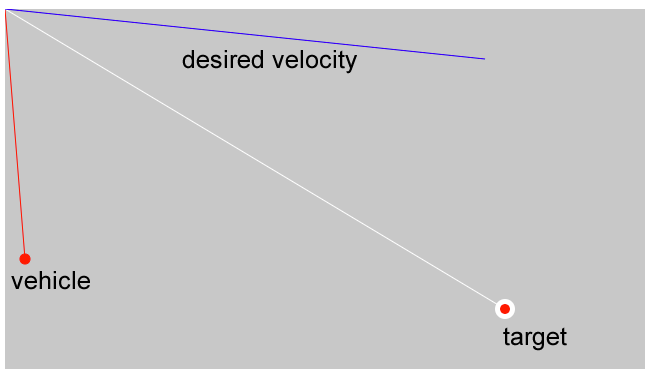
この例ではsetup()関数で全部行っているので、ビークルは一瞬でターゲットの位置に移動します。ここにアニメーション要素を持ちこむと、シーク動作が実現できます。
次のコードはシーク動作の例です。キャンバス上でマウスを動かすと、三角形(ビークル)がマウスカーソルに向かって移動します。
sketch.js
// Vehicleオブジェクト
let vehicle;
function setup() {
createCanvas(640, 360);
vehicle = new Vehicle(width / 2, height / 2);
}
function draw() {
background(200);
// マウスカーソルを探す
vehicle.seek(createVector(mouseX, mouseY));
// 位置を更新
vehicle.update();
// 乗り物を描画
vehicle.display();
}Vehicle.js
// Vehicleクラス
class Vehicle {
constructor(x, y) {
// 加速度、最初は0
this.acceleration = createVector(0, 0);
// 速度、最初は0
this.velocity = createVector(0, 0);
// 自分の位置、コンストラクタ関数に渡される変数x,y
this.location = createVector(x, y);
// 最大速度
this.maxspeed = 4;
// 最大の力、操舵力の制限に使用
this.maxforce = 0.1;
// ビークルのサイズ
this.r = 3.0;
}
// シーク操舵力アルゴリズム
seek(target) {
// 望まれる速度は、現在位置からターゲットの位置を指すベクトル
const desired = p5.Vector.sub(target, this.location);
// 正規化して向きの情報のみにする
desired.normalize();
// この乗り物は、最大速度でターゲットに向かって移動したいと思っている
// 最大速度でターゲットに向かう、望まれる速度を計算する
desired.mult(this.maxspeed)
// レイノルズの操舵力の公式
const steer = p5.Vector.sub(desired, this.velocity);
// 操舵力の大きさを制限する
steer.limit(this.maxforce);
// 操舵力を適用
this.applyForce(steer);
}
// ニュートンの第二法則:希望する場合には質量で割ることもできる
applyForce(force) {
this.acceleration.add(force);
}
// 標準的なEuler統合運動モデル
update() {
// 加速度は速度を変更する
this.velocity.add(this.acceleration);
// 速度を制限
this.velocity.limit(this.maxspeed);
// 速度は位置を変更する
this.location.add(this.velocity);
// 毎回、加速度を0にリセットする
this.acceleration.mult(0);
}
// 乗り物は速度の方向を指す三角形。上を指して描くので、90度足して回転させる
display() {
// ベクトルの回転角度 + 90度
const theta = this.velocity.heading() + PI / 2;
fill(175);
stroke(0);
// 変換の開始
push();
// 今の自分の位置を、座標の原点にする
translate(this.location.x, this.location.y);
// ベクトルの回転角度 + 90度だけ、座標を回転
rotate(theta);
// 乗り物を表す三角形を描画
beginShape();
vertex(0, -this.r * 2);
vertex(-this.r, this.r * 2);
vertex(this.r, this.r * 2);
endShape(CLOSE);
// 変換の終了
pop();
}
}これと同じような動作は三角関数などを使っても可能ですが、ベクトルを用いていることがこの例の特徴です。
Vehicleクラスのseek()メソッドで行っているのは、下図で表される、次のことです(赤線と文字”steer”は永井が追加)。
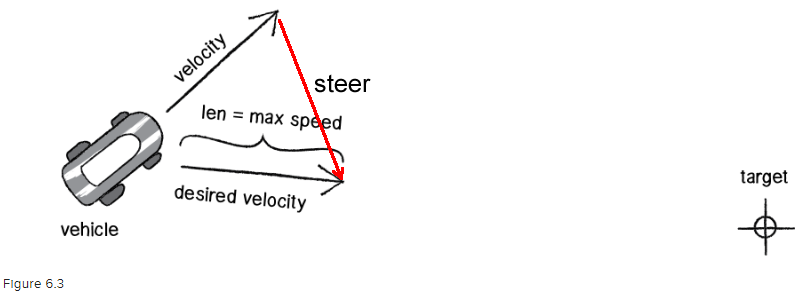
シーク操舵力アルゴリズム
- targetのベクトルからVehicleオブジェクトの現在位置のベクトルを引いて、希望するベクトルdesiredを求める
- desiredには速度を掛けるので、掛ける前にdesiredを正規化して、大きさの情報を1にする
- そのdesiredに最大速度を掛ける。これによりdesiredの大きさは最大速度(4)になる
- このdesiredからVehicleオブジェクトの速度を引く。これが毎フレーム、ターゲットに向かおうとする操舵力(steer)。
- このベクトルをapplyForce()メソッドに渡す。
分離:近いと避ける
ほかの相手ととぶつからないように距離をとる「分離」は、「6.11 Group Behaviors (or: Let’s not run into each other)」に、次のように説明されています(訳出:永井勝則)。
”レイノルズは言っています。「混雑を避けるために舵を切る」。言い換えると、あるビークルが別のビークルに非常に近い場合、そのビークルから離れる方向に舵を切るのです。聞いたことがありませんか? シークは、ビークルがターゲットの方向に向かう動作でした。つまり、シークの力を逆にすると逃げる動作になるのです”
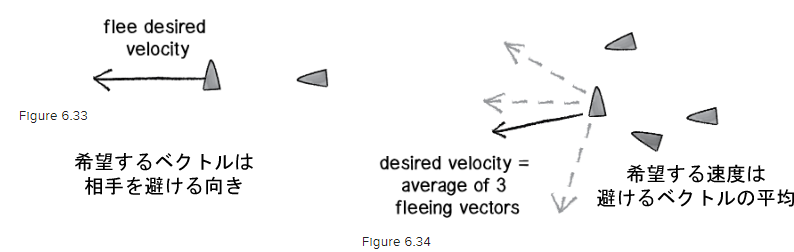
次のコードは、separate()メソッドを実装したVehicleクラスの例です。またビークルの数が多い方が分離の動作が確認しやすいので、ラッピング処理(端から出たら、逆の端から入れる)を行うborders()メソッドも追加しています。sketch.jsにはmouseDragged()関数を追加して、キャンバスの上のマウスドラッグで、Vehicleオブジェクトが作成できるようにしています。
sketch.js
// 作成したビークルを保持する配列
let vehicles;
function setup() {
createCanvas(640, 360);
vehicles = [];
// まずビークルを100個作成し、vehicles配列に入れる
for (let i = 0; i < 100; i++) {
const vehicle = new Vehicle(random(width), random(height));
vehicles.push(vehicle);
}
}
function draw() {
background(200);
// vehicles配列にある個々のビークルのメソッドを呼び出す
for (let i = 0; i < vehicles.length; i++) {
// 新しいメソッド2つ
vehicles[i].separate(vehicles);
vehicles[i].borders();
vehicles[i].update();
vehicles[i].display();
}
}
// マウスのドラッグで、乗り物を追加
function mouseDragged() {
const vehicle = new Vehicle(mouseX, mouseY);
vehicles.push(vehicle);
}Vehicle.js
// Vehicleクラス
class Vehicle {
constructor(x, y) {
// 加速度、最初は0
this.acceleration = createVector(0, 0);
// 速度、最初は0
this.velocity = createVector(0, 0);
// 自分の位置、コンストラクタ関数に渡される変数x,y
this.location = createVector(x, y);
// 最大速度
this.maxspeed = 4;
// 最大の力、操舵力の制限に使用
this.maxforce = 0.1;
// ビークルのサイズ
this.r = 3.0;
}
// シーク操舵力アルゴリズム
seek(target) {
// 望まれる速度は、現在位置からターゲットの位置を指すベクトル
const desired = p5.Vector.sub(target, this.location);
// 正規化して向きの情報のみにする
desired.normalize();
// このビークルは、最大速度でターゲットに向かって移動したいと思っている
// 最大速度でターゲットに向かう、望まれる速度を計算する
desired.mult(this.maxspeed)
// レイノルドの操舵力の公式
const steer = p5.Vector.sub(desired, this.velocity);
// 操舵力の大きさを制限する
steer.limit(this.maxforce);
// 操舵力を適用
this.applyForce(steer);
}
// ニュートンの第二法則:希望する場合には質量で割ることもできる
applyForce(force) {
this.acceleration.add(force);
}
// 標準的なEuler統合運動モデル
update() {
// 加速度は速度を変更する
this.velocity.add(this.acceleration);
// 速度を制限
this.velocity.limit(this.maxspeed);
// 速度は位置を変更する
this.location.add(this.velocity);
// 毎回、加速度を0にリセットする
this.acceleration.mult(0);
}
// ビークルは速度の方向を指す三角形。上を指して描くので、90度足して回転させる
display() {
// ベクトルの回転角度 + 90度
const theta = this.velocity.heading() + PI / 2;
fill(175);
stroke(0);
// 変換の開始
push();
// 今の自分の位置を、座標の原点にする
translate(this.location.x, this.location.y);
// ベクトルの回転角度 + 90度だけ、座標を回転
rotate(theta);
// ビークルを表す三角形を描画
beginShape();
vertex(0, -this.r * 2);
vertex(-this.r, this.r * 2);
vertex(this.r, this.r * 2);
endShape(CLOSE);
// 変換の終了
pop();
}
// 新しいメソッド、分離
separate(vehicles) {
// 近いと見なす距離
const desiredseparation = 20;
// 空のベクトルから開始
let sum = createVector(0, 0);
// 平均を出すため、ベクトルを足し、合計の数で割る
// 近すぎるビークルの数を追跡する必要がある
let count = 0;
for (let i = 0; i < vehicles.length; i++) {
// このビークルと、ほかのビークルとの距離
const d = p5.Vector.dist(this.location, vehicles[i].location);
// ほかのビークルが20ピクセル以内にいるなら
if ((d > 0) && (d < desiredseparation)) {
// ほかのビークルの位置からこのビークルへのベクトル
const diff = p5.Vector.sub(this.location, vehicles[i].location);
diff.normalize();
// ほかのビークルから離れる方向のベクトルの大きさとは?
// 近いなら逃げるべきで、遠いなら逃げなくてもよい。
// そこで、距離で割るという重み付けをする。
diff.div(d);
// ベクトルを全部足し、countをインクリメントする
sum.add(diff);
count++;
}
}
// 近いものがないときには何もする必要はない
// ゼロで割ることはできないのでこの条件が必要
if (count > 0) {
sum.div(count);
// 平均をmaxspeedにスケーリング
sum.setMag(this.maxspeed);
// レイノルズの操舵力の公式
const steer = p5.Vector.sub(sum, this.velocity);
steer.limit(this.maxforce);
// 力をビークルの加速度に適用
this.applyForce(steer);
}
}
// 数が多い方が分離の動作が分かりやすいので追加する
// ラッピング処理(端から出たら、逆の端から入れる)
borders() {
if (this.location.x < -this.r) this.location.x = width + this.r;
if (this.location.y < -this.r) this.location.y = height + this.r;
if (this.location.x > width + this.r) this.location.x = -this.r;
if (this.location.y > height + this.r) this.location.y = -this.r;
}
}ビークルは互いに避け合います。
separate()メソッドは、引数にビークルの配列vehiclesを受け取ります。このメソッドの目的は、ほかのビークルを調べて、近くにいるビークルについて避けるベクトルを求めてそれらを合算し、その平均を計算することです。平均のベクトルが分かれば、そこから操舵力が計算できます。合算するので、その元になるゼロのベクトルが、また平均するので、近くにいるビークルの総数が、それぞれ必要になります。
separate(vehicles) {
const desiredseparation = 20
let sum = createVector(0, 0);
let count = 0;変数desiredseparationは”近い”と見なす距離です。20を指定しているので、このビークルから20ピクセル以内にあるビークルを近いと見なします。変数sumはゼロベクトルで、合算するベクトルの元に使用します。変数countは近いと見なしたビークルのカウントアップに使用します。
for (let i = 0; i < vehicles.length; i++) {
const d = p5.Vector.dist(this.location, vehicles[i].location);
if ((d > 0) && (d < desiredseparation)) {
const diff = p5.Vector.sub(this.location, vehicles[i].location);
diff.normalize();
diff.div(d);
sum.add(diff);
count++;
}
}つづくforループでは、作成された全ビークルにアクセスし、このビークルと別のビークルとの距離をp5.Vector.dist()を使って調べます。そして(d > 0) && (d < desiredseparation)を条件として、ほかのビークルからこのビークルへのベクトルdiffを求めます。
(d > 0) && (d < desiredseparation)という条件をよく見ると、dが0の場合が含まれていないことが分かります。dが0とは、調べている対象が自分自身であることを意味します。自分自身はベクトルの合算にも総数にも加えたくないので、(d > 0) && (d < desiredseparation)は非常にうまい条件設定だと言えます。
diff.div(d)は重要性の差別化です。dの値が大きいほどdiffの大きさは小さくなり、合計の中での重要性も小さくなります。逆にdの値が小さいほどdiffの大きさは大きくなり、合計の中での重要性も大きくなります。その後sumにdiffを加え、countを1大きくします。forループが終わるときには、sumにcount個分のdiffが加えられます。
if (count > 0) {
sum.div(count);
sum.setMag(this.maxspeed);
const steer = p5.Vector.sub(sum, this.velocity);
steer.limit(this.maxforce);
this.applyForce(steer);
}
}平均のベクトルはsumをcountで割って算出するので、(count > 0)という条件は重要です。何かの拍子に1つだけ遠く離れたビークルがいるかも知れず、そのときcountは0なので、0で割るとエラーが発生します。
シーク + 分離
sketch.jsのdraw()関数のforループに、vehicles[i].seek(createVector(mouseX, mouseY))を追加すると、マウスカーソルに向かいつつも、互いが離れようとするビークルが作成できます。
function draw() {
background(200);
// vehicles配列にある個々のビークルのメソッドを呼び出す
for (let i = 0; i < vehicles.length; i++) {
vehicles[i].seek(createVector(mouseX, mouseY));
// 新しいメソッド2つ
vehicles[i].separate(vehicles);
vehicles[i].borders();
vehicles[i].update();
vehicles[i].display();
}
}またVehicleクラスのseparate()メソッドで使ったdesiredseparation変数に、Vehicleクラスのrプロパティを使用すると、rプロパティは描画する三角形のサイズに関係するので、ビークルのサイズに関連付けて分離動作が実行できます。
separate(vehicles) {
const desiredseparation = this.r * 3;下はその実行画面です。組み合わせることでまったく異なる動きになることが分かります。
ウルフラム セル・オートマトン(Wolfram CA)
スティーブン・ウルフラムの1次元セル・オートマトン(cellular automata)の単純なデモ(natureofcode.com)。
// セルの幅と高さ
const w = 10;
// 0と1の配列
let cells;
// ちょうど真ん中に、"1"の状態を持つセルを置いてスタート
let generation = 0;
// ルールセットを保持する配列。たとえば[0,1,1,0,1,1,0,1]
let ruleset = [0, 1, 0, 1, 1, 0, 1, 0];
function setup() {
createCanvas(640, 400);
cells = Array(floor(width / w));
for (let i = 0; i < cells.length; i++) {
cells[i] = 0;
}
// cells配列の真ん中の要素を1にする
cells[cells.length / 2] = 1;
}
function draw() {
for (let i = 0; i < cells.length; i++) {
if (cells[i] === 1) {
fill(200);
}
else {
fill(51);
noStroke();
rect(i * w, generation * w, w, w);
}
}
if (generation < height / w) {
generate();
}
}
// 新しい世代を作成する処理
function generate() {
// 新しい値を保持するための空の配列を作成
let nextgen = Array(cells.length);
// 全部の場所について、現在の状態と両隣りの状態を調べることによって、新しい状態を決める。
// 隣りが1つしかない端は無視する。
for (let i = 1; i < cells.length - 1; i++) {
let left = cells[i - 1]; // 左隣り
let me = cells[i]; // 現在の状態
let right = cells[i + 1]; // 右隣り
// ルールセットにもとづいて、新しい世代を計算する
nextgen[i] = rules(left, me, right);
}
// 新しい世代を現在の世代にする
cells = nextgen;
generation++;
}
// ウルフラムルールの実装
// もっと簡潔にできるが、場合ごとに分けた方が理解しやすい。
function rules(a, b, c) {
if (a == 1 && b == 1 && c == 1) return ruleset[0];
if (a == 1 && b == 1 && c == 0) return ruleset[1];
if (a == 1 && b == 0 && c == 1) return ruleset[2];
if (a == 1 && b == 0 && c == 0) return ruleset[3];
if (a == 0 && b == 1 && c == 1) return ruleset[4];
if (a == 0 && b == 1 && c == 0) return ruleset[5];
if (a == 0 && b == 0 && c == 1) return ruleset[6];
if (a == 0 && b == 0 && c == 0) return ruleset[7];
return 0;
}解説
ウルフラムのセル・オートマトンと聞いても、ほとんどの方が(わたしも含め)チンプンカンプンでしょうから、使われている言葉の意味から述べていきます。
(スティーブン・)ウルフラムはイギリス生まれの理論物理学者で、ウィキペディアによると、「1982年より、現在では『複雑系』に分類される自然界の複雑さについて研究。セル・オートマトンに関する革新的研究を行った。23歳のときにはセル・オートマトンに関する論文を出版した。」とあります。
セル・オートマトン
イモガイの貝殻の模様は、「隣の細胞が色素を分泌するか抑制するかによってその細胞自身が色素を分泌するかどうかが決まるという。ゆっくりとした成長と共にこのような反応が起こると、貝殻の縁に沿う細胞の帯は貝殻の表面に模様を残す。」そうです。

「自然界や社会には、このような「局所的なルールに基づいて相互作用した結果、大域的な秩序が形成される」例がよくみられる」。これを計算でシミュレーションしようとするのが、セル・オートマトンです(セルは細胞、オートマトンはからくりという意味)。
2状態 3近傍 1次元セル・オートマトン
1次元というのは、変化する方向が1つという意味で、[0,0,1,0,1]と言った1次元配列で表すことができます。2状態というのは、オンかオフ、白か黒、はたまた生か死か、コンピュータにとってみれば0か1で表されるということです。3近傍とは、自分と左右の両隣りを言います。
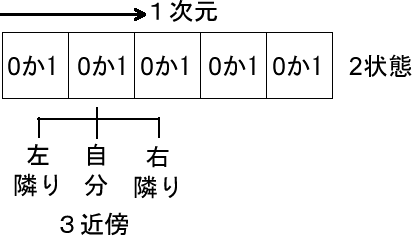
上図の左から2つめのセル(白枠)に注目してください。これを”自分”とします。すると、左隣りと右隣りのセルが定まります。この自分のセルの次の状態は、左隣りと右隣りのセルの状態によって決まります。もちろん自分のセルは左から2つめのセルだけでなく、そのほかのセルも自分の対象になります。つまり、時間の経過とともにセルの次の状態が、その左右のセルの状態によって決まっていくのです。
ルールセット
下図のような初期状態のセルの集まり(1次元配列)があったとします。状態が1のセル(me)に注目すると、その左右(keftとright)が決まります。
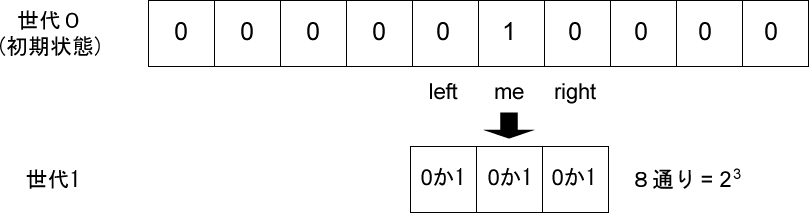
この3つのセルはどれも0か1の状態を持つので、その組み合わせは次の8通りがあります。
(1,1,1)、(1,1,0)、(1,0,1)、(1,0,0)、(0,1,1)、(0,1,0)、(0,0,1)、(0,0,0)
これに、状態を更新するルールを適用します。下図は、1を黒、0を白で表した3つのセルの真ん中(me)に、左右どちらかのセル1つが黒ならmeは黒に、そうでないならmeは白になる、というルールを適用した結果を示しています。
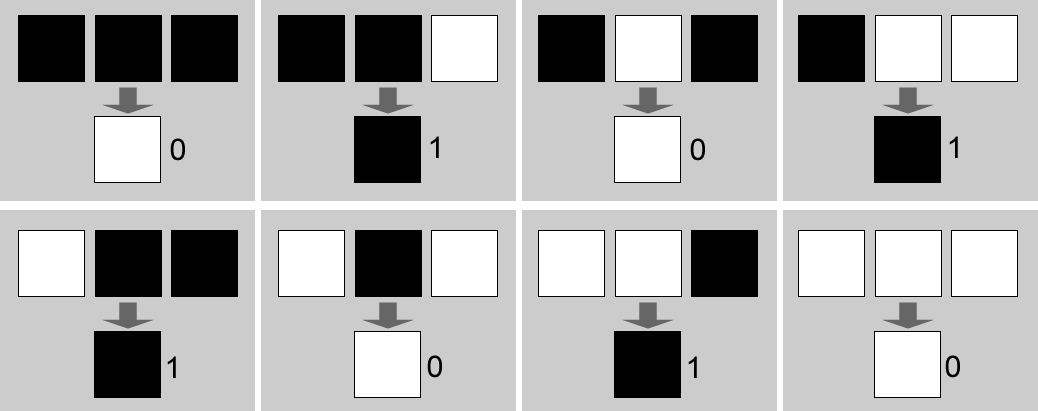
このルールはまた、配列の形式で表すことができます。
[0,1,0,1,1,0,1,0]
この、上図の数字を順に配列に並べたものをルールセットと言います。
セルの集まりの最初の状態を[0,0,0,0,0,1,0,0,0,0]として、[0,1,0,1,1,0,1,0]というルールセットを適用すると、1回めの適用でセルの集まりは、たとえば次のように変化し(世代1)、2回めの適用で次のように変化します(世代2)。この繰り返し(次の世代の作成、描画)が、「非常に単純化されたモデルであるが、生命現象、結晶の成長、乱流といった複雑な自然現象を模した、驚くほどに豊かな結果を与えてくれる」という結果になるのです。
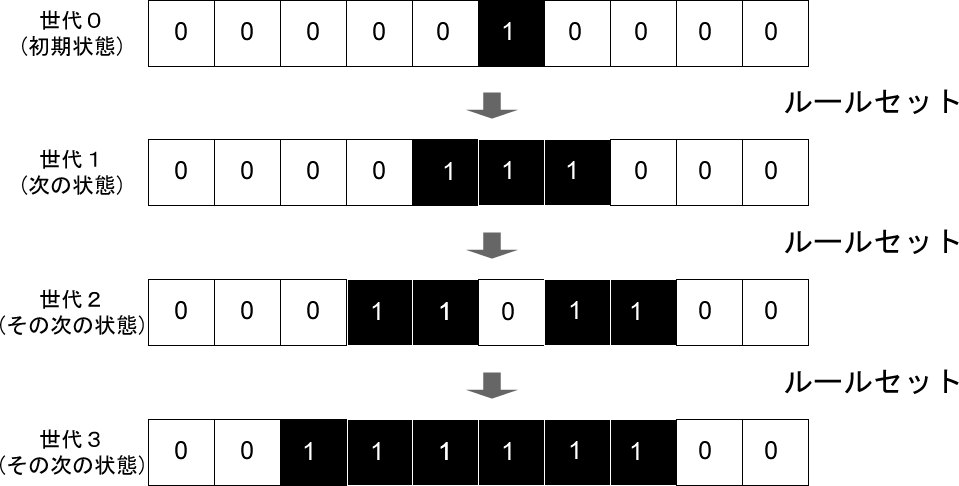
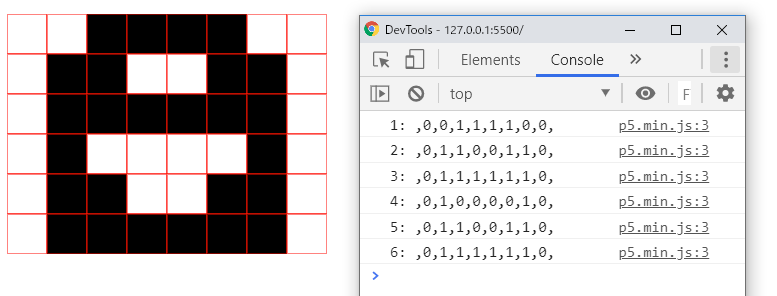
次のコードは、ここまでをまとめた、簡単な例です。
// セルの状態を保持する配列
let cells = [0, 0, 0, 0, 1, 1, 0, 0, 0, 0];
// 描画するセルの幅と高さ
const cellW = 40;
// meとleftとrightが全部白なら、次のmeは白に、
// また、meとleftとrightが全部黒なら、次のmeは白に、
// それ以外なら、次のmeは黒になる
const ruleset = [0, 1, 1, 1, 1, 1, 1, 0];
function setup() {
// 320 x 240 なので、40 x 40の正方形が8個 x 6個描画できる。
// drawGeneration()を1フレーム当たり6回呼び出すと、
// ちょうどキャンバスの高さ分が描画できることになる。
createCanvas(320, 240);
background(240);
stroke(255, 0, 0);
// draw()関数は1回だけ実行
noLoop();
}
function draw() {
background(200);
// drawGeneration()を1フレーム当たり、6回呼び出す。
drawGeneration(1);
drawGeneration(2);
drawGeneration(3);
drawGeneration(4);
drawGeneration(5);
drawGeneration(6);
}
// 世代数を受け取り、次世代の配列を求め、cells配列に割り当てる
function drawGeneration(level) {
// cells配列の要素数を持つ、次世代用配列を新たに作成
let nextgen = Array(cells.length);
// iを1から始め、i < cells.length - 1までインクリメントすることで、
// 左と右隣りのセルを持たない両端のセルを対象にしない
// => cells配列は要素を10個持つが、次世代の計算対象にするのは、両端を除く8個
for (let i = 1; i < cells.length - 1; i++) {
const left = cells[i - 1]; // 自分の左隣り
const me = cells[i]; // 自分
const right = cells[i + 1]; // 自分の右隣り
// rules()関数の結果を、nextgen[インデックス]として保持
nextgen[i] = rules(left, me, right);
// 値が0なら塗り色を白、1なら黒にする
if (nextgen[i] === 0) {
fill(255);
}
else if (nextgen[i] === 1) {
fill(0);
}
// その色で矩形を描画
rect((i - 1) * cellW, (level - 1) * cellW, cellW, cellW);
}
// nextgen配列を、次のcells配列にする
cells = nextgen;
// 確認用 '世代番号: 配列'
print(level + ': ' + cells);
}
// ルールセット
function rules(a, b, c) {
if (a == 1 && b == 1 && c == 1) return ruleset[0]; // 黒、黒、黒 => 白
if (a == 1 && b == 1 && c == 0) return ruleset[1]; // 黒、黒、白 => 黒
if (a == 1 && b == 0 && c == 1) return ruleset[2]; // 黒、白、黒 => 黒
if (a == 1 && b == 0 && c == 0) return ruleset[3]; // 黒、白、白 => 黒
if (a == 0 && b == 1 && c == 1) return ruleset[4]; // 白、黒、黒 => 黒
if (a == 0 && b == 1 && c == 0) return ruleset[5]; // 白、黒、白 => 黒
if (a == 0 && b == 0 && c == 1) return ruleset[6]; // 白、白、黒 => 黒
if (a == 0 && b == 0 && c == 0) return ruleset[7]; // 白、白、白 => 白
return 0;
}
ライフゲーム
ジョン・コンウェイによるライフゲームのセル・オートマトンの基本的な実装(natureofcode.com)
let w; // 描く正方形の1辺の長さ
let columns; // 描くグリッドの列数
let rows; // 描くグリッドの行数
let board; // 描画する内容を保持する2D配列
let next; // board配列の入れ替えに使用する
function setup() {
createCanvas(720, 400);
w = 20;
// キャンバスの幅と高さ、描く矩形の幅と高さから、行数と列数を割り出す
columns = floor(width / w);
rows = floor(height / w);
// 2D配列を作成する奇抜な方法
board = new Array(columns);
for (let i = 0; i < columns; i++) {
board[i] = new Array(rows);
}
// 2D配列の入れ替えに使用する
next = new Array(columns);
for (let i = 0; i < columns; i++) {
next[i] = new Array(rows);
}
init();
}
function draw() {
background(255);
generate();
for (let i = 0; i < columns; i++) {
for (let j = 0; j < rows; j++) {
if ((board[i][j] === 1)) fill(0);
else fill(255);
stroke(0);
rect(i * w, j * w, w - 1, w - 1);
}
}
}
// マウスプレスでboardをリセット
function mousePressed() {
init();
}
// board配列をランダムに埋める
function init() {
for (let i = 0; i < columns; i++) {
for (let j = 0; j < rows; j++) {
// 碁盤目の上下左右の端を0にする
if (i == 0 || j == 0 || i == columns - 1 || j == rows - 1) board[i][j] = 0;
// 残りをランダムに0と1で埋める
else board[i][j] = floor(random(2));
// next配列の2次元めの配列の要素は全部0にする
next[i][j] = 0;
}
}
}
// 新しい世代を作成する処理
function generate() {
// 2D配列の上下左右の端を除いて走査
// 対象セルはboard[x][y]
for (let x = 1; x < columns - 1; x++) {
for (let y = 1; y < rows - 1; y++) {
// 対象セルの周囲9つのセルの値を調べ、合計する
// ただし対象セル自体の値も含んでいる
let neighbors = 0;
for (let i = -1; i <= 1; i++) {
for (let j = -1; j <= 1; j++) {
neighbors += board[x + i][y + j];
}
}
// 上のループで対象セル自体の値も加算したので、その分を引く
neighbors -= board[x][y];
// 生死のルール
if ((board[x][y] == 1) && (neighbors < 2)) next[x][y] = 0; // 過疎
else if ((board[x][y] == 1) && (neighbors > 3)) next[x][y] = 0; // 過密
else if ((board[x][y] == 0) && (neighbors == 3)) next[x][y] = 1; // 誕生
else next[x][y] = board[x][y]; // 生存
}
}
// 2次元配列の入れ替え
let temp = board;
board = next;
next = temp;
}画面のクリックでリスタートできます。
解説
「ライフゲーム」と呼ばれてはいますが、これはいわゆるゲームではありません。前のサンプルの配列を2次元にしたセル・オートマトンで、実は歴史的には、前のサンプルのウルフラム以前に行われた研究です。ウィキペディアの「ライフゲーム」によると、
ライフゲーム (Conway’s Game of Life) は1970年にイギリスの数学者ジョン・ホートン・コンウェイ (John Horton Conway) が考案した生命の誕生、進化、淘汰などのプロセスを簡易的なモデルで再現したシミュレーションゲームである。単純なルールでその模様の変化を楽しめるため、パズルの要素を持っている。
生物集団においては、過疎でも過密でも個体の生存に適さないという個体群生態学的な側面を背景に持つ。セル・オートマトンのもっともよく知られた例でもある。
とあります。
ライフゲームのルール
前のサンプルは、2状態、3近傍の1次元セル・オートマトンでしたが、ライフゲームは2状態、8近傍の2次元セル・オートマトンです。状態は1(生きている)と0(死んでいる)で表され、これを水平と垂直の2方向に変化する2次元配列に保持します。そして、自分の周囲にある合計8つのセルの状態から、自分の次の状態が決まります。
ライフゲームでは、次のルールで自分の次の状態が決まります(ライフゲームより)。
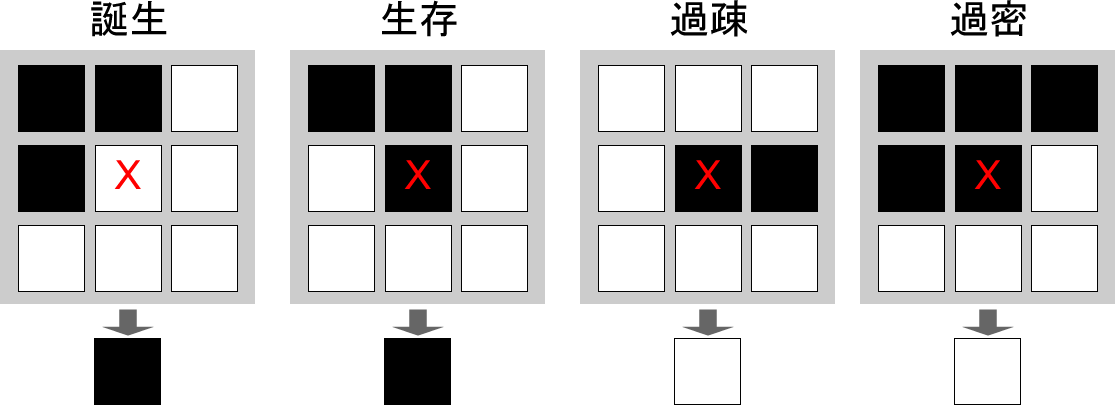
- 誕生
死んでいるセルに隣接する生きたセルがちょうど3つあれば、次の世代が誕生する。 - 生存
生きているセルに隣接する生きたセルが2つか3つならば、次の世代でも生存する。 - 過疎
生きているセルに隣接する生きたセルが1つ以下ならば、過疎により死滅する。 - 過密
生きているセルに隣接する生きたセルが4つ以上ならば、過密により死滅する。
下図はルールの例です。自分(対象セル)はX、生きているセルは黒四角、死んでいるセルは白四角で表しています。
ルールのコード
ライフゲームのルールのコードは上記サンプルのgenerate()関数内にあります。
// ライフのルール
// 過疎(Loneliness)
// 生きているセルに隣接する生きたセルが1つ以下ならば、過疎により死滅する。
if ((board[x][y] == 1) && (neighbors < 2)) {
next[x][y] = 0;
// 過密(Overpopulation)
// 生きているセルに隣接する生きたセルが4つ以上ならば、過密により死滅する。
}
else if ((board[x][y] == 1) && (neighbors > 3)) {
next[x][y] = 0;
// 誕生(Reproduction)
// 死んでいるセルに隣接する生きたセルがちょうど3つあれば、次の世代が誕生する。
}
else if ((board[x][y] == 0) && (neighbors == 3)) {
next[x][y] = 1;
}
else {
// 生存(Stasis)
// 生きているセルに隣接する生きたセルが2つか3つならば、次の世代でも生存する。
next[x][y] = board[x][y];
}しかしここで難しいのは、対象とするセルの周囲8つのセルを特定する方法です。次のコードはそれを説明するためのものです。
8近傍セルへのアクセス(自分も含む)
function setup() {
// テスト用の2次元配列
// 上下左右の端を全部0にしてある
const board = [
[0, 0, 0, 0, 0],
[0, 'a', 'b', 'c', 0],
[0, 'd', 'e', 'f', 0],
[0, 'g', 'h', 'i', 0],
[0, 0, 0, 0, 0]
];
// 上下左右の端を除いて走査
for (let x = 1; x < 5 - 1; x++) {
for (let y = 1; y < 5 - 1; y++) {
let neighbors = '';
let count = 1;
// 対象となるセル
const target = board[x][y];
print('target: ' + target)
// 対象セルの周囲9つのセルの値を調べ、合計する
// ただし対象セル自体の値も含んでいる
for (let i = -1; i <= 1; i++) {
for (let j = -1; j <= 1; j++) {
// 対象セルの周囲9つのセル(対象自体も含む)を足していく
neighbors += board[x + i][y + j];
print('count: ' + count);
print('i :' + i);
print('j :' + j);
print('neighbors: ' + neighbors);
count++;
}
}
}
}
}ここで使用している2次元配列boardは、8近傍のセルにうまくアクセスできるように、内側の最初の配列と最後の配列の要素が全部0、その間の配列の最初と最後の要素が0という特殊な構造をしています。
ここで使用しているforループは実に4重で、非常に複雑です。こういう場合は、変数に値を割り当て、繰り返しを1つずつ見ていくことが、正確な理解の助けになります。
このコードを実行すると、次の結果が出力されます。

これを元に、ループの初回、つまりXとyが1のときの各変数の変化を見ていきます。xとyが1ということは、board[x][y]に当てはめるとboard[1][1]になるので、これはaを指しています。つまり、x=1、y=1のときの対象セルはaだということです。
3つめのループとその内側のループの変数iとjは、-1から1までインクリメントされます。初回のループではiとjは-1なので、[x + i][y + j]は[1-1][1-1] => [0][0]となり、board[0][0]は左上隅のセルになります。ここではこの値0が文字列として、変数neighborsに連結されていきます。
その次のループでは、i=-1、j=0なので、board[0][1]になります。これはaの真上のセルを指しています。そしてこの値0が連結され、neighborsは”00″になります。
次の表はXとyが1のときのこの変化をまとめたものです。
| カウント | i | j | board[x+i][y+i] | neighborsの値 | そのセルはどれか |
|---|---|---|---|---|---|
| 1 | -1 | -1 | [1-1][1-1] = [0,0] | “0” | 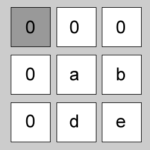 |
| 2 | -1 | 0 | [1-1][1+0] = [0,1] | “00” | 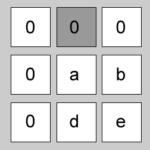 |
| 3 | -1 | 1 | [1-1][1+1] = [0,2] | “000” | 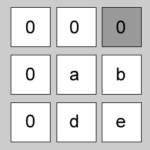 |
| 4 | 0 | -1 | [1+0][1-1] = [1,0] | “0000” | 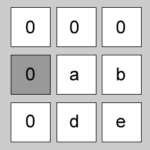 |
| 5 | 0 | 0 | [1+0][1+0] = [1,1] | “0000a” | 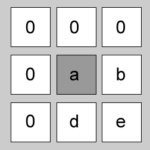 |
| 6 | 0 | 1 | [1+0][1+1] = [1,2] | “0000ab” | 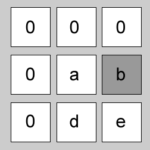 |
| 7 | 1 | -1 | [1+1][1-1] = [2,0] | “0000ab0” | 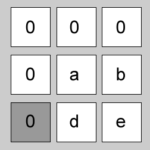 |
| 8 | 1 | 0 | [1+1][1+0] = [2,1] | “0000ab0d” |  |
| 9 | 1 | 1 | [1+1][1+1] = [2,2] | “0000ab0de” | 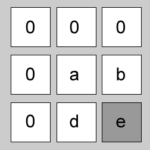 |
この例からは、for (let i = -1; i <= 1; i++)と for (let j = -1; j <= 1; j++) を使用すると、board[x][y]を対象セルとする、自身も含む周囲の9つのセルが参照できることが分かります。 実際には、変数neighborsには1か0が加算されるので、前述したライフゲームのルールに使用できます。
対象セルを除外する
上記ループでは、対象セル(a)も含めていたので、それを除外する必要があります。一見面倒な気がしますが、neighborsで欲しいのは合計なので、単純にneighborsからboard[x][y]を引くだけです。
// 上のループで対象セル自体の値も加算したので、その分を引く
neighbors -= board[x][y];2次元配列を作成する方法
2次元配列は、上記サンプルで使われている方法に加え、次の方法でも作成できます。
// 2次元配列を作成する従来の方法
let x, y;
const boardA = new Array(columns);
for (y = 0; y < columns; y++) {
boardA[y] = new Array(rows);
for (x = 0; x < rows; x++) {
boardA[y][x] = 0;
}
}
// 2次元配列を作成する新しい方法
const boardB = new Array(columns).fill().map(() => {
return new Array(rows).fill(0);
});セルの値を0か1でランダムに埋める方法
上記サンプルで使われているように、p5.jsのfloor()とrandom(2)で簡単に実現できます。
for (let i = 0; i < columns; i++) {
for (let j = 0; j < rows; j++) {
// セルを1か0でランダムに埋める
board[i][j] = floor(random(2));
}
}複数のパーティクルシステム
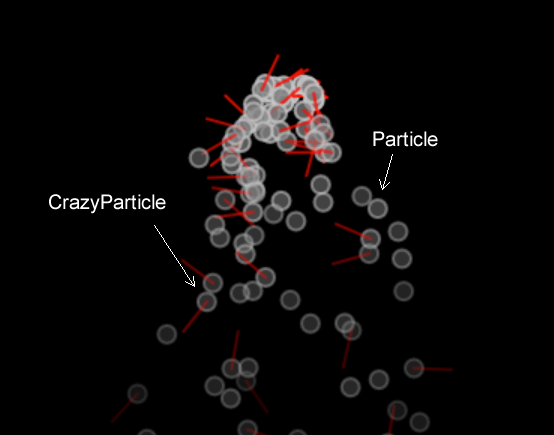
画面をクリックすると、マウス位置にパーティクルの噴出が1つ作成されます。それぞれの噴出は、Particlesクラスとそのサブクラス、CrazyParticlesクラスを持つパーティクルシステムのインスタンスです。ここでは継承とポリモーフィズムが使われている点に注目してください。オリジナルはダニエル・シフマン。
sketch.js
// パーティクルシステムを管理するただの配列
let systems;
function setup() {
createCanvas(710, 400);
systems = [];
}
function draw() {
background(0);
// このforループはsystems.lengthが0の場合は実行されない。
for (i = 0; i < systems.length; i++) {
// systems配列に含まれるParticleSystemインスタンスの
// run()とaddParticle()メソッドを呼び出す
systems[i].run();
systems[i].addParticle();
}
// systems配列が空の場合には、画面に文字を描画する。
if (systems.length === 0) {
fill(255);
textAlign(CENTER);
textSize(32);
text("クリックしてパーティクルシステムを追加", width / 2, height / 2);
}
}
// 画面がクリックされたら、
function mousePressed() {
// ParticleSystem
const pSystem = new ParticleSystem(createVector(mouseX, mouseY));
systems.push(pSystem);
}Particle.js
// Particleクラス
// // 前の「パーティクルシステム」のParticleクラスとほぼ同じ
class Particle {
constructor(position) {
this.acceleration = createVector(0, 0.05);
this.velocity = createVector(random(-1, 1), random(-1, 0));
this.position = position.copy();
this.lifespan = 255.0;
}
run() {
this.update();
this.display();
}
update() {
this.velocity.add(this.acceleration);
this.position.add(this.velocity);
this.lifespan -= 2;
}
display() {
stroke(200, this.lifespan);
strokeWeight(2);
fill(127, this.lifespan);
ellipse(this.position.x, this.position.y, 12, 12);
}
isDead() {
if (this.lifespan < 0) {
return true;
}
else {
return false;
}
}
}CrazyParticle.js
// CrazyParticleクラス
// Particleクラスのサブクラス
class CrazyParticle extends Particle {
constructor(origin) {
// スーパークラス(Particle)のコンストラクタを呼び出す。
super(origin);
// スーパークラスにはないこのクラス独自のプロパティ。角度の値に使用する
this.theta = 0.0;
}
// スーパークラスのupdate()メソッドをオーバーライド
update() {
// スーパークラスのupdate()メソッドを呼び出す。
super.update();
// その後、独自の動作を加える
// 水平方向の速度にもとづいて、回転をインクリメント
this.theta += (this.velocity.x * this.velocity.mag()) / 10.0;
}
// スーパークラスのdisplay()メソッドをオーバーライド
display() {
// スーパークラスのdisplay()メソッドを呼び出す。
super.display();
// その後、独自の動作を加える。
// 回転する線
push();
translate(this.position.x, this.position.y);
rotate(this.theta);
// 区別しやすいように線を赤くする
stroke(255, 0, 0, this.lifespan);
line(0, 0, 25, 0);
pop();
}
// run()メソッドはParticleクラスから継承され、オーバーライドせずそのまま使用するので、
// ここで定義する必要はない。
}注意
CrazyParticleクラスはParticleクラスを継承するので、CrazyParticle.jsファイルはParticle.jsより後に読む込む必要があります。そうしないと「Particleが定義されていない」という参照エラーが発生します。
index.htmlの<script>タグ
<script src="js/Particle.js"></script>
<script src="js/CrazyParticle.js"></script>
<script src="js/ParticleSystem.js"></script>解説
これは、前出の「パーティクルシステム」を発展させ、同じクリックで、別のパーティクルを描画できるようにしたサンプルです。元の「パーティクルシステム」で使われたParticleSystem.jsとParticle.jsに大きな違いはありませんが、Particleクラスを継承するCrazyParticleクラスが追加されています。
パーティクルが動いていると区別しづらいですが、白い丸がParticleクラスのインスタンスで、白い丸に赤い線がついているのがCrazyParticleクラスのインスタンスです。
解説
このプログラムはオブジェクト指向プログラミングと呼ばれる方法で書かれています。オブジェクト指向プログラミングについては「オブジェクト指向 JavaScript 入門」などのページが参考になります。
スピログラフ
このスケッチでは、簡単な変換を使って、連動する円によるスピログラフ風効果を作成しています。スペースキーを押すとトレース(線描)と、それを作成している形状(円)の表示が切り替わります。サンプル作成はR. Luke DuBois。
// 1度にいくつの事柄を行うか
let NUMSINES = 20;
// すべての現在の角度を保持する配列
let sines = new Array(NUMSINES);
// 現在の角度の半径の初期値
let rad;
// カウンタ変数
let i;
// 次の値を変更すると、何を行っているかが分かる
let fund = 0.005; // 元になる角度のスピード(角速度)
let ratio = 1; // 次の角速度を決める乗数
let alpha = 50; // 線描する場合の不透明度
let trace = false; // 線描するかどうか
function setup() {
createCanvas(710, 400);
// 元になるセンターの円の半径を決める
rad = height / 4;
background(204);
// sines配列はNUMSINES個の要素を持つ
for (let i = 0; i < sines.length; i++) {
// 配列要素としてPI(180度)を入れる
// 全部北向きで始める
sines[i] = PI;
}
}
function draw() {
// 線描しない場合
if (!trace) {
// ジオメトリ(円)を表示する場合には画面をクリアする
background(204);
// 黒いペン(線を不透明の黒にする)
stroke(0, 255);
// 塗はなし
noFill();
}
// メインのアクション
push(); // 変換行列を開始
translate(width / 2, height / 2); // 画面センターに移動
for (let i = 0; i < sines.length; i++) {
// 円の中の小さな"点"の半径、これが線描時のペン先になる
let erad = 0;
// 線描時の設定
if (trace) {
stroke(0, 0, 255 * (float(i) / sines.length), alpha); // 青
fill(0, 0, 255, alpha / 2); // 青
// ペン先の幅を角度に関係付けて決める
erad = 5.0 * (1.0 - float(i) / sines.length);
}
// 円の半径
let radius = rad / (i + 1);
// 円を回転
rotate(sines[i]);
// 線描しない場合は円を描く
if (!trace) ellipse(0, 0, radius * 2, radius * 2);
push(); // 1レベル上がる
translate(0, radius); // 円の端に移動
// 線描しない場合は小さな円を描画
if (!trace) ellipse(0, 0, 5, 5);
// 線描する場合はeradの半径で円を描画
if (trace) ellipse(0, 0, erad, erad);
pop(); // 1レベル下がる
translate(0, radius); // 次の位置に移動
// 基準にもとづいて角度を更新
sines[i] = (sines[i] + (fund + (fund * i * ratio))) % TWO_PI;
}
pop(); // 最後の変換を戻す
}
function keyReleased() {
if (key == ' ') {
trace = !trace;
background(255);
}
}スペースキーは、一度画面をクリックしてから押します。
解説
スピログラフとは、歯車の穴にボールペンなどを指して歯車を回すことで複雑な模様が簡単に描ける定規を言います。言葉で説明するよりも下の写真を見た方がピンとくるでしょう。左がスピログラフで、右がスピログラフで描いた図形です。
上記サンプルで使われているコードは短いですが、描くスピログラフの数が可変的なので、決して簡単ではありません。そこで、大小2つの円で曲線を描く、シンプルなコードを以下に示します。描く円の数が決まっているので、配列やforループを使う複雑さが排除できます。また多重的なpush()とpop()の使用も理解しやすくなります。
// スペースキーの押し下げで、線描か円を描画するかを切り替える
// 角度の数値
let sineValue1;
let sineValue2;
// 円の半径
let rad1;
let rad2;
// 角速度
let fund1 = 0.005;
let fund2 = 0.05;
// ペン先になる小さな円の半径
const smallRad = 3;
// トレース(線描)するかどうか
let trace = false;
function setup() {
createCanvas(500, 400);
noFill();
sineValue1 = PI;
sineValue2 = PI;
rad1 = height / 4;
rad2 = rad1 / 2;
// noLoop();
}
function draw() {
// 線描しない場合 => 円を描画する場合
if (!trace) {
// 前のフレームの描画は消す必要がある
background(204);
// 線の色は黒
stroke(0);
noFill();
// 線描する場合は
}
else {
// 線の色は赤
stroke(255, 0, 0);
// 塗りは緑
fill(0, 255, 0);
}
push();
translate(width / 2, height / 2);
rotate(sineValue1);
// 線描しない場合は、
if (!trace) {
// 大きな円を描く
ellipse(0, 0, rad1 * 2, rad1 * 2);
}
push();
translate(0, rad1);
// 小さな円を線描
// 線描しない場合は、黒の線、塗りはなしで描画
// 線描する場合は、赤の線、塗りは緑で描画
ellipse(0, 0, smallRad * 2, smallRad * 2);
// 線描しない場合は、
if (!trace) {
// 2番めに大きな円を描く
ellipse(0, 0, rad2 * 2, rad2 * 2);
}
push();
rotate(sineValue2);
translate(0, rad2);
// 小さな円を線描
ellipse(0, 0, smallRad * 2, smallRad * 2);
pop();
pop();
pop();
sineValue1 += fund1;
sineValue2 += fund2;
}
// 押されたキーが放されたら
function keyReleased() {
// そのキーがスペースキーなら
if (key === ' ') {
// 変数traceを反転
trace = !trace;
// この瞬間の描画を、背景色でクリアする
// 線描の場合、draw()でbackground()が呼び出せないので、
// ここで呼び出す
background(255);
}
}スペースキーは、一度画面をクリックしてから押します。
スペースキーを押さない最初の状態で表示される円のアニメーションは、「7_6:円運動 p5.js JavaScript」で見たようなサインとコサインの計算で行っているのではなく、毎フレーム、 translate()とrotate()関数で座標システムを操作し、回転する角度を変えていることによるものです。
そしてスピログラフ風の曲線を実際に描いているのは、半径がsmallRadの小さな円です。小さな円の軌跡が曲線になります。これは、スペースキーを何度かすばやく押して、線描と円の描画を切り替えると分かります。
まず最初のpush()関数で、最初の変換が始まります。これは座標システムの原点をキャンバスセンターに移す変換と、座標システムを180度回転させる変換です。線描しない場合(traceがfalseのとき)には、キャンバスセンターを中心とする半径rad1の円が描かれます。
push();
translate(width / 2, height / 2);
rotate(sineValue1);
// 線描しない場合は、
if (!trace) {
// 大きな円を描く
ellipse(0, 0, rad1 * 2, rad1 * 2);
}座標システムを180度回転させると、ちょど下図のように、上下左右が逆になります。

translate()関数については「5_1:移動(translate) p5.js JavaScript」で、rotate()関数については「5_2:回転(rotate) p5.js JavaScript」で述べています。
そしてつづく変換では、上図の座標システムの状態で、原点が(0,100)だけ移動します。ここを中心に、ごく小さな円と2番めに大きな円が描かれます。
push();
translate(0, rad1);
// 小さな円を線描
ellipse(0, 0, smallRad * 2, smallRad * 2);
// 線描しない場合は、
if (!trace) {
// 2番めに大きな円を描く
ellipse(0, 0, rad2 * 2, rad2 * 2);
}
最後の変換では、180度の回転と、(0, rad2)分の移動が行われます。座標システムが再度180度回転するので、元の状態に戻ります。
push();
rotate(sineValue2);
translate(0, rad2);
ellipse(0, 0, smallRad * 2, smallRad * 2);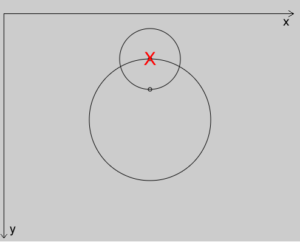
draw()関数では、180度を代入したsineValue1とsineValue2に、それぞれfund1とfund2が足されていくので、座標システムは毎フレーム、その角度分の回転を繰り返します。fund1とfund2の値は異なるので、2番めに大きな円の方が大きな円よりも速く回転して見えることになります。
実際のスピログラフでは、小さな円が大きな円より外に出ることはないので、厳密にはスピログラフのシミュレーションとは言えないのかもしれませんが、このサンプルではこのように座標変換を複層的に使って(親の因果が子に報うように)、スピログラフ風の曲線描画を行っています。
L-system(Lindenmayer system、エルシステム)
このスケッチは、Lindenmayer system、いわゆるL-systemにもとづいて自動的な描画を行います。L-systemはよく、自然や幾何学に見られる興味深い”フラクタルスタイル”のパターンを作成するプロシージャルグラフィックスで使用されます。サンプル作成はR. Luke DuBois。
// タートル関連:
let x, y; // タートルの現在の位置
let currentangle = 0; // タートルの向き
let step = 20; // 1つの'F'でいくつ移動するか
let angle = 90; // 向きを変えるときの角度
// L-systemに関係する変数
let thestring = 'A'; // "axiom"、つまり開始する文字列
let numloops = 5; // 計算する回数
let therules = []; // ルールの配列
therules[0] = ['A', '-BF+AFA+FB-']; // 1つめのルール
therules[1] = ['B', '+AF-BFB-FA+']; // 2つめのルール
let whereinstring = 0; // 読み取る文字列のインデックス位置
function setup() {
createCanvas(710, 400);
background(255);
stroke(0, 0, 0, 255);
// 左下隅から開始
x = 0;
y = height - 1;
// L-systemを計算
for (let i = 0; i < numloops; i++) {
thestring = lindenmayer(thestring);
}
}
function draw() {
// 文字列内の現在対象となっている1文字を描画する
drawIt(thestring[whereinstring]);
// 今読み取っているストリング内での位置をインクリメント
// 端で折り返し
whereinstring++;
if (whereinstring > thestring.length - 1) whereinstring = 0;
}
// L-systemを解釈
function lindenmayer(s) {
let outputstring = ''; // 空の出力文字列で開始
// 記号の一致を探して、therulesを走査
for (let i = 0; i < s.length; i++) {
let ismatch = 0; // デフォルトで、一致しない
for (let j = 0; j < therules.length; j++) {
if (s[i] == therules[j][0]) {
outputstring += therules[j][1]; // 置換を書き込む
ismatch = 1; // 一致したので、記号をコピーしない
break; // このforループから抜ける
}
}
// 一致しない場合は、記号をコピー
if (ismatch == 0) outputstring += s[i];
}
return outputstring; // 修正した文字列を返す
}
// タートルコマンドを描画するカスタム関数
function drawIt(k) {
// 文字が'F'なら前進を描画
if (k === 'F') {
// stepとcurrentangleを元に、極座標を直交座標に変換
let x1 = x + step * cos(radians(currentangle));
let y1 = y + step * sin(radians(currentangle));
line(x, y, x1, y1); // 古い点と新しい点を線で結ぶ
// タートルの位置を更新
x = x1;
y = y1;
// 文字が'+'なら左を向く
}
else if (k === '+') {
currentangle += angle;
// 文字が'-'なら右を向く
}
else if (k === '-') {
currentangle -= angle;
}
// ランダムなカラー値を得る
let r = random(128, 255);
let g = random(0, 192);
let b = random(0, 50);
let a = random(50, 100);
// 半径の正規分布を算出
let radius = 0;
radius += random(0, 15);
radius += random(0, 15);
radius += random(0, 15);
radius = radius / 3;
// 円を描画
fill(r, g, b, a);
ellipse(x, y, radius, radius);
}解説
”エルシステム”という言葉とサンプルコード、その説明書きを読んですぐ理解できる人はおそらくごく少数でしょう。(わたしも含め)ほとんどの方にはチンプンカンプンだと思われるので、ここでもごく基本を見ていくことにします。
その前にまず、説明書きに使われている用語がよく分かりません。以下は専門ページに書かれていたものの引用です。
フラクタル:樹木や雲、海岸線などの自然界にある複雑な形状を、同じパターンの図形で表す数学的概念。フラクタルによって描かれる図形は、全体像と図形の一部分が相似になる性質がある(ASCII.jpデジタル用語辞典)。
プロシージャル:日本語では「手続き型」と訳され、数式や処理を組み合わせ、何らかの操作を行うこと全般をプロシージャルという。具体的にはプロシージャルテクスチャ(画像の生成)、プロシージャルアニメ(数式による制御、スクリプトや条件定義などによるアニメーション)などの手法がある(デジタルハリウッド CG用語辞典)。
L-system
ウィキペディアによると、L-systemは、「形式文法の一種で、植物の成長プロセスを初めとした様々な自然物の構造を記述・表現できるアルゴリズムである。自然物の他にも、反復関数系(Iterated Function System; IFS)のようないわゆる自己相似図形やフラクタル図形を生成する場合にも用いられる。L-System は1968年、ハンガリーユトレヒト大学の理論生物学者にして植物学者であったアリステッド・リンデンマイヤー(Aristid Lindenmayer)により提唱され、発展した」とあります。
L-systemは、G = {V, S, ω, P} で定義され、各要素は次の意味を持ちます。
- V:文字や記号の、L-systemによる成長を表す文字列
- S:変化しない定数
- ω:開始する文字(axiom)。L-systemの成長はこの文字から始まる
- P:置換ルール。A(置換前) -> AB(置換後)のように表される。
たとえば、開始文字のωが’F’で、置換ルールのPがF->Fだとします。F->Fは、FはFに置換される、という意味なので、実際には何も変化せず、成長もありません。したがって結果のVは’F’のままです。
しかし置換ルールを、たとえばF->F+Fにすると、FはF+Fに置換されるので、Vは変化することになります。以下はその説明です。
(L-system適用の1回め)
FはF+Fに置換されるので、Vは’F+F’になる。
(L-system適用の2回め)
1回めの適用で生まれた’F+F’に対して、ルールF->F+Fを適用する。これは(すべての)’F’を’F+F’に置換する、という意味なので、’F+F’は、’F+F+F+F’になる。
具体的にいうと、’F+F’の1つめの文字に対してルールを適用するかどうかが検討される。1つめの文字は’F’で、これはルールに適合する(‘F’は’F’なので、’F+F’に置換できる)。適用後の結果は’F+F’になる。
次いで2つめの文字’+’が検討される。’+’は’F’ではないので、ルールは適用されない。したがって’+’のまま変化しない。
3つめの文字’F’も1つめの’F’と同様、ルールが適用され、’F+F’に置換される。
次の文字はもうないので、ルールの適用はこれで終わり、’F+F’と’+’、’F+F’を連結した’F+F+F+F’が、結果の(次の世代の)文字列となる。
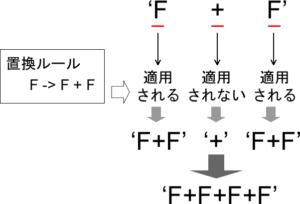
(L-system適用の3回め)
2回めの適用で生まれた’F+F+F+F’に対して、ルールF->F+Fを適用する。すべての’F’が’F+F’に置換され、’+’は’+’のままなので、結果は’F+F+F+F+F+F+F+F’になる。
ここまでの3回の適用で、最初の文字’F’は’F+F+F+F+F+F+F+F’に成長したことになります。この文字列の1文字ずつに対し、たとえば’F’の場合には線を描いて進み、’+’の場合には90度左に向きを変える、といった計算を行うと、フラクタルな図形を描くことができます。
描画の例
上記サンプルと「Drawing fractals in the browser with L-systems and ES6」ページを参考に、ウィキペディアの「L-system」ページの「例4:コッホ曲線」で説明されている次の内容を、p5.jsで描画してみます。
例4:コッホ曲線
直角で構成されるコッホ曲線の描画例。
V : F
S : +, -;
ω: F
P : (F → F+F-F-F+F)
上記において、F はタートルによる直線の描画、+ はタートルを左へ90°回転、同じく- は右へ90°回転する事を意味する。これを順次計算すると、以下のような図形が得られる。

以下はその実装コードです。
// L-systemに関係する変数
// ruleはFプロパティとその値を持つオブジェクト
const rule = {
F: 'F+F-F-F+F'
};
let systemState;
// タートルの描画に関する変数
let x, y; // タートルの現在の位置
let whereinstring = 0; // 読み取る文字列のインデックス位置
let currentangle = 0; // タートルの向き
let step = 10; // 1つの'F'でいくつ移動するか
let angle = 90; // 向きを変えるときの角度
function setup() {
createCanvas(700, 500);
background(200);
// キャンバス左上隅近くからスタート
x = 10;
y = 10;
const axiom = 'F';
// L-systemで計算し、各世代の文字列を得る
// F => F+F-F-F+F
const stateString1 = renderAGeneration(axiom);
print(stateString1);
// F+F-F-F+F => F+F-F-F+F+F+F-F-...
const stateString2 = renderAGeneration(stateString1);
print(stateString2);
// F+F-F-F+F+F+F-F-... => F+F-F-F+F+F+F-F-F+F-...
const stateString3 = renderAGeneration(stateString2);
print(stateString3);
systemState = stateString1;
//systemState = stateString2;
//systemState = stateString3;
}
// 与えられた1文字にルールを適用して返す。
// ルールが設定されていない1文字の場合はそのまま返す
function applyRule(char) {
// ruleは{F: "F+F-F-F+F"}オブジェクト
// charはF,+,-
// print(rule[char]);
// プロパティアクセサー([]、ブラケット表記法)は、オブジェクトのプロパティへのアクセスを提供する。
// https://developer.mozilla.org/ja/docs/Web/JavaScript/Reference/Operators/Property_Accessors
// ruleオブジェクトにはFプロパティのみ定義されているので、rule['F']の場合には、その値'F+F-F-F+F'が返される。
// rule['+']とrule['-']の場合には、ruleに+と-プロパティは定義されていないので結果はundefinedとなり、'+'か'-'がそのまま返される。
return rule[char] || char;
}
// 現在の状態文字列のすべての文字にルールを適用して返す
function renderAGeneration(previousGeneration) {
let nextGeneration = '';
// previousGenerationオブジェクトのプロパティを取り出しその値を処理する
// characterはプロパティの値
for (const character of previousGeneration) {
// previousGenerationの全文字を1文字ずつapplyRule()に渡し、
// その結果を連結する
nextGeneration += applyRule(character);
}
// 連結した結果の文字列を返す
return nextGeneration;
}
function draw() {
// 文字列内の現在対象となっている1文字を描画する
// 文字列の文字へのアクセス => 文字列を配列のようなオブジェクトとして扱い、数値の添字を用いる方法です。 (ECMAScript 5 で導入)
// https://developer.mozilla.org/ja/docs/Web/JavaScript/Reference/Global_Objects/String#Character_access
// systemState文字列のwhereinstring番めの単一文字がdrawIt()関数に渡される
//print(systemState[whereinstring]);
drawIt(systemState[whereinstring]);
// 今読み取っているストリング内での位置をインクリメント
whereinstring++;
// 端で折り返し
if (whereinstring > systemState.length - 1) {
whereinstring = 0;
}
}
// タートルコマンドを描画するカスタム関数
function drawIt(k) {
// 文字が'F'なら前進を描画
if (k === 'F') {
// stepとcurrentangleを元に、極座標を直交座標に変換
let x1 = x + step * cos(radians(currentangle));
let y1 = y + step * sin(radians(currentangle));
// 古い点と新しい点を線で結ぶ
line(x, y, x1, y1);
// タートルの位置を更新
x = x1;
y = y1;
// 文字が'+'なら
}
else if (k === '+') {
// 左を向く
currentangle += angle;
// 文字が'-'なら右を向く
}
else if (k === '-') {
//print('-')
currentangle -= angle;
}
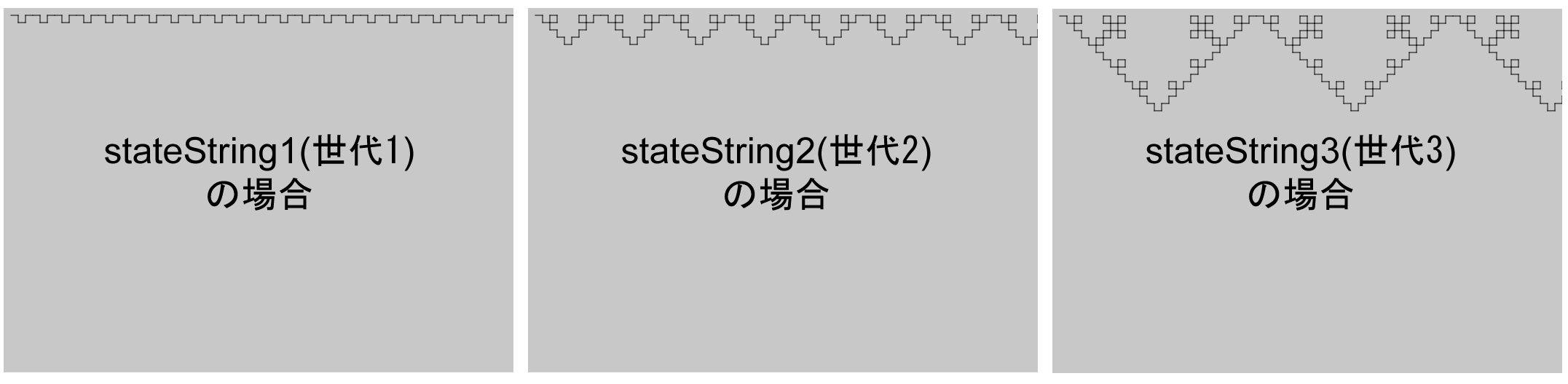
}下図は、左から、変数systemStateにstateString1とstateString2、stateString3を代入して実行した結果です。JavaScriptではY軸方向が下向きになるので、ウィキペディアの「例4:コッホ曲線」の図とは上下が逆になりますが、それをのぞけば同様の結果です。
ばね
水平バー(白い横長の矩形)をクリック、ドラッグ、リリースするとばね運動をシミュレーションします。
// トップバーのばねの描画に関係する変数
const springHeight = 32;
const maxHeight = 200,
minHeight = 100;
let left, right;
// マウスがトップバーに重なっているかどうか
let over = false;
// トップバーが移動状態にあるかどうか
let move = false;
// ばねのシミュレーションに関係する定数
const M = 0.8, // 質量
K = 0.2, // ばね定数
D = 0.92, // 減衰
R = 150; // 静止しているときの位置(=>自然な状態での長さ)
// ばねのシミュレーションに関係する変数
let ps = R, // 位置 => 最初はR(自然な状態)
vs = 0.0, // 速度
as = 0, // 加速度
f = 0; // 力
function setup() {
createCanvas(710, 400);
rectMode(CORNERS);
noStroke();
left = width / 2 - 100;
right = width / 2 + 100;
}
function draw() {
background(102);
updateSpring();
drawSpring();
}
function drawSpring() {
// 台を描画
fill(0.2); // 塗りをほぼ黒に
let baseWidth = 0.5 * ps + -8; // 台の幅と高さはpsの値によって変化する
rect(width / 2 - baseWidth, ps + springHeight, width / 2 + baseWidth, height);
// カラーを設定し、トップバーを描く
// overかmoveの一方または両方がtrueなら => overとmoveがともにfalseでなければ
if (over || move) {
// 塗りを白に
fill(255);
}
else {
// そうでなければ塗をグレーに
fill(204);
}
rect(left, ps, right, ps + springHeight);
}
function updateSpring() {
// ばねの位置を更新
if (!move) {
// f=-ky => ばねの復元力:力(f)は-ばね定数(-K)*(現在位置-静止位置)
f = -K * (ps - R);
// 加速度: ニュートンの第二法則(物体の加速度は、加えた力に比例し、その質量に反比例する)
// f=ma => a=f/m 加速度は、力/質量
as = f / M;
// 速度:(今の速度+加速度)に減衰率を掛ける
vs = D * (vs + as);
// 新しい位置:新しい速度に現在位置を足す
ps = ps + vs;
}
// 速度が微小の場合は0にする
if (abs(vs) < 0.1) {
vs = 0.0;
}
// マウスがトップバー上にあるかどうかを調べる
if (mouseX > left && mouseX < right && mouseY > ps && mouseY < ps + springHeight) {
over = true;
}
else {
over = false;
}
// トップバーがドラッグされて移動状態にあるなら
if (move) {
// トップバーの高さの真ん中を、移動するマウスカーソルに合わせる => トップバーがマウスの動きに合わせて上下する
ps = mouseY - springHeight / 2;
// と同時に、psの上下の移動量を制限して、トップバーが必要以上に上下移動しないようにする
ps = constrain(ps, minHeight, maxHeight);
}
// 参考用にキャンバス左上隅にps値を描画
stroke(255, 0, 0);
text('ps: ' + ps, 20, 20);
noStroke();
}
// マウスが押されたら
function mousePressed() {
// マウスがトップバー上にあるなら
if (over) {
move = true;
}
}
// マウスが放されたら
function mouseReleased() {
move = false;
}解説
ばね運動のシミュレーションとして、上記サンプルでは、次の定数と変数が使用されています。
| 定数 | 値 | 意味 |
|---|---|---|
| M | 0.8 | 質量。トップバー(白い矩形)の重さ。 |
| K | 0.2 | ばね定数。そのばねの伸びにくさを表す。大きいほど伸ばすのに強い力が要る。 |
| D | 0.92 | 減衰率。ばねの伸び縮みはやがて止まる。 |
| R | 150 | 自然長。ばねが静止しているときの自然な長さ。 |
| 変数 | 初期値 | 意味 |
|---|---|---|
| ps | R | 位置 |
| vs | 0.0 | 速度 |
| as | 0 | 加速度 |
| f | 0 | 力 |
これらは次のように使用されます。
f = -K * (ps - R);
as = f / M;
vs = D * (vs + as);
ps = ps + vs;f = -K * (ps – R)は、「フックの法則」を使った、ばねの復元力(弾性力)を求める計算です。力(f)は-ばね定数(-K)*(現在位置-静止位置)で計算できます。
as = f / Mは、ニュートンの第二法則(物体の加速度は、加えた力に比例し、その質量に反比例する)と呼ばれる運動方程式f=maを使って、加速度を求める式です(a=f/m)。 今、質量と力が分かっているので、加速度が計算できます。
vs = D * (vs + as)は、次のフレームでの速度の計算です。今の速度(右辺のvs)に上で求めた加速度を足すと、次の瞬間の速度が分かりますが、ばねはやがて止まるので、ここでは減衰率(0.92)を掛けています。
ここまで計算してきて、次のフレームでのばねの位置が、ps = ps + vs で分かります。
次のコードはシンプルにしたばね運動の例です。リセットボタンで再開できます。
// ばねのシミュレーションに関係する定数
const M = 0.8, // 質量
K = 0.2, // ばね定数
D = 0.9, // 減衰
R = 130; // 静止しているときの位置(=>自然な状態での長さ)
// ばねのシミュレーションに関係する変数
let ps = 300, // 位置 => 最初はキャンバス下端まで引き延ばされている
vs = 0.0, // 速度
as = 0, // 加速度
f = 0; // 力
function setup() {
createCanvas(300, 300);
fill(0);
// リセットボタン
const resetButton = setButton('リセット', {
x: 220,
y: 280
});
// psを初期値に戻す => ばねは下に引き延ばされた状態になる
resetButton.mousePressed(() => {
ps = 300;
});
}
function draw() {
background(200);
// 変数を更新
updateSpring();
// 更新した変数を使って描画
drawSpring();
}
function drawSpring() {
// ばね部
stroke(250);
line(150, 10, 150, ps);
noStroke();
// 重り部
ellipse(150, ps, 30, 30);
// 参考用にキャンバス左上隅にps値を描画
text('ps: ' + ps, 20, 20);
}
// ばねの位置を更新
function updateSpring() {
// 鉛直ばね振り子
// http://www.wakariyasui.sakura.ne.jp/p/mech/tann/banehuriko.html
// f=-ky => ばねの復元力:力(f)は-ばね定数(-K)*(現在位置-自然長)
// psは最初300なので、力が生じる。
f = -K * (ps - R);
// 加速度: ニュートンの第二法則(物体の加速度は、加えた力に比例し、その質量に反比例する)
// f=ma => a=f/m 加速度は、力/質量で計算できる
as = f / M;
// 速度:(今の速度+加速度)に減衰率を掛ける(ばねの伸縮はやがて止まる)
vs = D * (vs + as);
// 新しい位置:新しい速度に現在位置を足す
ps = ps + vs;
// 速度が微小の場合は0にする。速度は正負両方あるのでabs()関数で絶対値にする
if (abs(vs) < 0.1) {
vs = 0.0;
}
}
// ボタンを作成、設定して返す(要p5.dom.jsライブラリ)
function setButton(label, pos) {
const button = createButton(label);
button.size(80, 30);
button.position(pos.x, pos.y);
return button;
}なお、実際のばねはやがて止まりますが、シミュレーションでは、コンピュータがずっと計算をつづけるので、切りを見つけてばねを止める必要があります。次のコードはその意味で重要です。
// 速度が微小の場合は0にする
if (abs(vs) < 0.1) {
vs = 0.0;
}複数のばね
円はマウスでドラッグできます。マウスを放すと、円はばね運動を実行して元の位置に戻ります。(https://processing.org/examples/springs.htmlから移植)
sketch.js
const num = 3; // ばねの数は3つ
const springs = [num]; // 要素数が3の配列springsを作成
function setup() {
createCanvas(710, 400);
noStroke();
// Springクラスのインスタンスを3つ作成してsprings配列に入れる
// 引数 => (x位置、y位置、直径、減衰率、質量、ばね定数、Springインスタンスを入れる配列、ID)
// IDはsprings配列のインデックス番号と同じにする必要がある(SpringクラスのotherOver()メソッドの仕様により)
springs[0] = new Spring(240, 260, 40, 0.98, 8.0, 0.1, springs, 0);
springs[1] = new Spring(320, 210, 120, 0.95, 9.0, 0.1, springs, 1);
springs[2] = new Spring(180, 170, 200, 0.90, 9.9, 0.1, springs, 2);
}
function draw() {
background(51);
// draw()中はずっと、springs配列に含まれている3つのSpringインスタンスの
// update()とdisplay()メソッドを呼び出しつづける
for (let i = 0; i < num; i++) {
springs[i].update();
springs[i].display();
}
}
// ウィンドウがマウスプレスされたら(キャンバスだけでなく)
function mousePressed() {
// springs配列に含まれる3つのSpringインスタンスのpressed()メソッドを呼び出す
for (let i = 0; i < num; i++) {
springs[i].pressed();
}
}
// ウィンドウがマウスリリースされたら
function mouseReleased() {
// springs配列に含まれる3つのSpringインスタンスのreleased()メソッドを呼び出す
for (let i = 0; i < num; i++) {
springs[i].released();
}
}Spring.js
// Spring クラス
// (x位置、y位置、直径、減衰率、質量、ばね定数、Springインスタンスを入れる配列、ID)
class Spring {
constructor(_x, _y, _s, _d, _m, _k_in, _others, _id) {
this.x_pos = this.tempxpos = _x; // x位置
this.y_pos = this.tempypos = _y; // y位置
// this.size = 20; // 円の直径
this.size = _s; // 円の直径
this.over = false; // マウスがこのインスタンスと重なっているかどうか
this.move = false; // このインスタンスが移動中かどうか
// ばねのシミュレーションに関係する定数
this.mass = _m; // 自分の質量
// this.k = 0.2; // ばね定数
this.k = _k_in; // ばね定数
this.damp = _d; // 減衰率
this.rest_posx = _x; // 自然な状態にあるときのx位置
this.rest_posy = _y; // 自然な状態にあるときのy位置
// ばねのシミュレーションに関係する変数
//float pos = 20.0; // Position
this.velx = 0.0; // x方向の速度
this.vely = 0.0; // y方向の速度
this.accel = 0; // 加速度
this.force = 0; // 力
this.friends = _others; // 自分も含むSpringインスタンスを入れた配列
this.id = _id; // 自分のID(ほかとの区別に使用)
}
update() {
if (this.move) {
this.rest_posy = mouseY;
this.rest_posx = mouseX;
}
// y方向について、新しい位置を求める
// 力:f=-ky、-ばね定数()*(現在位置-自然長)
this.force = -this.k * (this.tempypos - this.rest_posy);
// 加速度:f=ma => a=f/m 加速度は力/質量
this.accel = this.force / this.mass;
// 速度:(今の速度+加速度)に減衰率を掛ける
this.vely = this.damp * (this.vely + this.accel);
// 新しい位置:新しい速度に現在位置を足す
this.tempypos = this.tempypos + this.vely;
// x方向について、新しい位置を求める
this.force = -this.k * (this.tempxpos - this.rest_posx);
this.accel = this.force / this.mass;
this.velx = this.damp * (this.velx + this.accel);
this.tempxpos = this.tempxpos + this.velx;
// over状態にあるかどうかは、毎フレーム、調べる必要がある
// マウスがこのインスタンスと重なっているか移動中の状態にあり、
// かつ、ほかのインスタンスがover状態にないなら、
if ((this.overEvent() || this.move) && !(this.otherOver())) {
// このインスタンスはover状態にある
this.over = true;
// そうでなければこのインスタンスはover状態にない
}
else {
this.over = false;
}
}
// マウスがこのSpringインスタンスと重なっているかどうか調べる
overEvent() {
// マウスとの距離
let disX = this.tempxpos - mouseX;
let disY = this.tempypos - mouseY;
let dis = createVector(disX, disY);
// 距離が半径より小さいなら
if (dis.mag() < this.size / 2) {
// マウスは重なっている
return true;
}
else {
// そうでなければ重なっていない
return false;
}
}
// ほかのSpringインスタンスがアクティブ状態にないことを確認する
otherOver() {
for (let i = 0; i < num; i++) {
// 対象が自分以外なら
if (i != this.id) {
// その対象がover状態なら
if (this.friends[i].over === true) {
// ほかのインスタンスのどれかがアクティブ状態にある
return true;
}
}
}
// ほかのインスタンスはどれもアクティブ状態にない
return false;
}
// 円を描画する
display() {
// over状態ならグレー
if (this.over) {
fill(153);
// over状態でないなら白
}
else {
fill(255);
}
ellipse(this.tempxpos, this.tempypos, this.size, this.size);
}
// ウィンドウがマウスプレスされたタイミングで呼び出される
pressed() {
// over状態なら
if (this.over) {
// 移動中
this.move = true;
}
else {
// 移動中でない
this.move = false;
}
}
// ウィンドウがマウスリリースされたタイミングで呼び出される
released() {
this.move = false;
this.rest_posx = this.x_pos;
this.rest_posy = this.y_pos;
}
}解説
Springクラスでは、上の「ばね」で見たのと同様の、ばね運動に関係するプロパティが定義されています。Springクラスのインスタンスはupdate()メソッドの中で、ばね運動の物理的な計算を行い、自分の位置を決めます。
ばねのシミュレーションとは直接関係ありませんが、このサンプルの秀逸な点は、overとmoveプロパティの設定とその扱い方にあります。複数の円はキャンバスに描かれたただのピクセルデータなので、どの円がマウスに重なっているかは実際に計算する必要があります。円にはこのover状態のほかに移動中かどうかを表すmove状態もあり、その論理的な組み合わせの構築は、実は非常に難しい作業です。このサンプルで使われているこの方法は、ほかのプログラミングでも応用できるので、覚えておいて損はありません。
なお、p5.jsのサンプルは、移植元と動作が違っているので、上記Springクラスでは、移植元を参考に、tempxposとtempyposプロパティを加えて書き直しています。


