目次
斜面に対する反射
processing.org/examplesからの、David Blitzによる”Reflection 1“サンプルの移植版。式(R = 2N(N・L)-L)にもとづく。Rは反射ベクトル、Nは法線ベクトル、Lは入射ベクトル。
// 床の左端の位置
let base1;
// 床の右端の位置Position of right hand side of floor
let base2;
// 移動するボールに関係する変数
let position;
let velocity;
let r = 6;
let speed = 3.5;
function setup() {
createCanvas(710, 400);
fill(128);
base1 = createVector(0, height - 150);
base2 = createVector(width, height);
// 円を画面中央の上端で開始
position = createVector(width / 2, 0);
// 最初の速度をランダムに計算
velocity = p5.Vector.random2D();
velocity.mult(speed);
}
function draw() {
// 背景を描画
fill(0, 12);
noStroke();
rect(0, 0, width, height);
// ベースを描画
fill(200);
quad(base1.x, base1.y, base2.x, base2.y, base2.x, height, 0, height);
// ベース上面の法線ベクトルを計算
let baseDelta = p5.Vector.sub(base2, base1);
baseDelta.normalize();
let normal = createVector(-baseDelta.y, baseDelta.x);
let intercept = p5.Vector.dot(base1, normal);
// 円を描画
noStroke();
fill(255);
ellipse(position.x, position.y, r * 2, r * 2);
// 円を移動
position.add(velocity);
// 正規化された入射ベクトル
incidence = p5.Vector.mult(velocity, -1);
incidence.normalize();
// ベースとの衝突を判定して処理する
if (p5.Vector.dot(normal, position) > intercept) {
// 入射ベクトルとベース上面との内積を計算
let dot = incidence.dot(normal);
// 反射ベクトルを計算して方向ベクトルに割り当てる
velocity.set(
2 * normal.x * dot - incidence.x,
2 * normal.y * dot - incidence.y,
0
);
velocity.mult(speed);
// 衝突点でベース上面の法線を描画
stroke(255, 128, 0);
line(
position.x,
position.y,
position.x - normal.x * 100,
position.y - normal.y * 100
);
}
// 境界との衝突の判定
// 右
if (position.x > width - r) {
position.x = width - r;
velocity.x *= -1;
}
// 左
if (position.x < r) {
position.x = r;
velocity.x *= -1;
}
// 上
if (position.y < r) {
position.y = r;
velocity.y *= -1;
// ベース上面をランダムに作成
base1.y = random(height - 100, height);
base2.y = random(height - 100, height);
}
}解説
コード量は少ないものの、大学受験で数学を選択する受験生程度の知識とやる気を必要とする、難度の高いサンプルです。まず、ベクトルの理解が必要です。ベクトルを表すp5.Vectorクラスについては「9:シミュレーション 1/2 (Simulate)」で述べています。
内積
次に必要なのが内積の理解です。内積(Dot product)は、「Vector Math Tutorial」ページに次のように説明されています。
内積は、2つのベクトル間の角度の計算に使用できるベクトル演算です。
float Vector2f_dot(Vector2f vector1, Vector2f vector2) { return vector1.x * vector2.x + vector1.y * vector2.y; }内積にはいくつかの興味深い特性があります。正規化された2つのベクトルの内積を取ると、acos(dotProduct)を使って、ベクトル間の角度を得ることができます(acos関数は、cos関数の逆を実行します。つまりx座標を取って、角度を返します)。
その内積は正規化された2つのベクトル間の角度のコサインなので、その2つのベクトルが互いにどれくらい似ているかの判断にも使用できます。2つのベクトルのなす角が直角である場合、その内積は0に等しくなります。90度未満の場合には正になり、90度より大きい場合には負になります。2つのベクトルが同じである場合には、ベクトルの大きさの2乗に等しくなります。
わたしの場合、高校の数学で習った記憶もあるのですが、内容は覚えていません。「数学:内積ってなんぞ? その1(物理と導入編)」に分かりやすい図説がありました。
内積の意味


(1)は、人間がトロッコを線路に沿ったベクトルbの方向に、1の力で押しているところです。1の力で押すと|b|(ベクトルbの大きさ)だけ進みます。
しかし(2)で、ベクトルbの方向に押せなくなったので、斜めから押すことにしました。
斜めというのは、ベクトルbの方向に対するθ度の角度で、|a|の力で押しました(3)。このときトロッコはベクトルbの方向にどれだけ進むのか? これが計算できるのが内積です。
また「内積の意味」ページには、「内積は、ベクトルbが、ベクトルaの方向に、ベクトルaとともに行った仕事の量である」とも説明されています。
内積の計算
内積を求めるには、p5.Vectorクラスのdot()メソッドを使用します。
function setup() {
createCanvas(400, 300);
background(200);
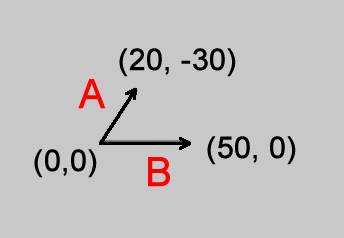
// ベクトルA
const A = createVector(20, -30);
// ベクトルB
const B = createVector(50, 0);
// ベクトルが表示できるように原点を移動
translate(100, 100);
// ベクトルA
line(0, 0, A.x, A.y);
// ベクトルB
line(0, 0, B.x, B.y);
// p5.Vector.dot()を使った、ベクトルAとベクトルBの内積の計算
const dot1 = p5.Vector.dot(A, B);
print(dot1);
// 手計算
const dot2 = A.x * B.x + A.y * B.y;
print(dot2);
}上記コードからは1000が出力されます。
内積の計算には、実は2つのベクトル間の角度は必要ありません。p5.Vector.dot()を使用するか、dot2を求める計算で使っている、掛けて掛けて足す(A.x * B.x + A.y * B.y)ことで得られます(前述の「数学:内積ってなんぞ? その1(物理と導入編)」参照)。「Vector Math Tutorial」ページで内積の計算に使われているコードもこの方法によるものです。

内積の使い道
ベクトルの向きが分かる
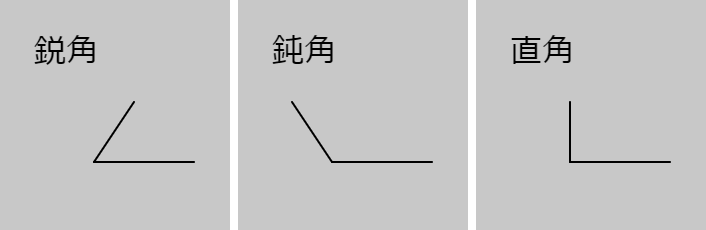
ベクトル同士の内積で、ベクトルの向きが分かります。内積では、ベクトル間の角度は小さい方の角度(0度以上180度以下)が使用されます。内積の値が正の場合には、2つのベクトル間の角度は90度より小さく(鋭角)、負の場合には90度より大きく(鈍角)、0の場合には90度だと判断できます。
以下はこれを確認するコードです。
// 内積の使い道
// 2つのベクトルの向きが分かる
function setup() {
createCanvas(400, 300);
background(200);
textSize(16);
// ベクトルA
// 鋭角
//const A = createVector(20, -30);
// 鈍角
//const A = createVector(-20, -30);
// 直角
const A = createVector(0, -30);
// ベクトルB
const B = createVector(50, 0);
// ベクトルが表示できるように原点を移動
translate(100, 100);
// ベクトルA
line(0, 0, A.x, A.y);
// ベクトルB
line(0, 0, B.x, B.y);
// ベクトルAとベクトルBの内積
const dot = p5.Vector.dot(A, B);
if (dot > 0) {
text('鋭角', -30, -50);
}
else if (dot < 0) {
text('鈍角', -30, -50);
}
else if (dot === 0) {
text('直角', -30, -50);
}
}
両方を単位ベクトルにすると、角度が分かる
2つのベクトルを両方とも、大きさが1の単位ベクトルにして内積を計算すると、それが2つのベクトル間の角度になります。
これを式から考えると、内積は、A・B = |A||B|cosθ です。今|A|も|B|も1なので、1*1*cosθ、つまりcosθ になる、というわけです。
次のコードはこの例です。あらかじめ60度の角をなすベクトルを作成し、それらを正規化してから内積を求め、acos()とdegrees()関数を使って、度数を計算しています。
// 内積の使い道
// 両方を単位ベクトルにすると、角度が分かる
function setup() {
createCanvas(400, 300);
background(200);
textSize(16);
// angle度の角をなすベクトルを作成
const angle = 60;
const radius = 60;
// (0,0)を中心とする半径60の円の円周上にある、angle度の座標を求める
const x = cos(radians(angle)) * radius;
const y = sin(radians(angle)) * radius;
// ベクトルA。分かりやすいようにy値は反転
const A = createVector(x, -y);
// ベクトルB
const B = createVector(radius, 0);
// ベクトルが表示できるように原点を移動
translate(100, 100);
// 2つのベクトルを描画
// ベクトルA
line(0, 0, A.x, A.y);
line(0, 0, B.x, B.y);
fill('red');
text('θ', 8, -1);
// ベクトルAとBを正規化
const An = A.normalize();
// print(An.mag()); // 大きさは1
const Bn = B.normalize();
// print(Bn.mag());
// 正規化した2つのベクトルの内積を計算
const dot = p5.Vector.dot(An, Bn);
// print(dot); // 0.5 => これはcosθの値
const radianValue = acos(dot); // acos()関数でラジアン単位の度数を得る
// console.log(radianValue) // 1.04719... これはラジアン単位
const degreeValue = degrees(radianValue);
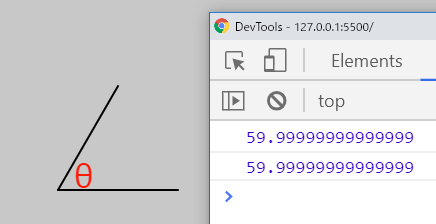
print(degreeValue); // 59.9999... 60度が得られた
print(degrees(acos(dot))); // 59.9999... 60度が得られた
}angle変数に度数を代入すると、その角度でベクトルを表す線が描かれ、内積から計算した度数が出力されます。
ベクトルAと単位ベクトルとの内積で、ベクトルAの、単位ベクトル方向への成分が分かる
これを、A・B = |A||B|cosθ に当てはめると、今|B|は1なので、右辺は|A|*1*cosθ、つまり|A|cosθ となります。これは後述するAの単位ベクトルへの射影です。
これは、次のようなコードで確認できます。
// 内積の使い道
// ベクトルAと単位ベクトルとの内積で、ベクトルAの、単位ベクトル方向への成分が分かる
function setup() {
createCanvas(400, 300);
background(200);
// ベクトルA
const A = createVector(20, -30);
// ベクトルB
const B = createVector(50, 0);
// ベクトルが表示できるように原点を移動
translate(100, 100);
// ベクトルA
line(0, 0, A.x, A.y);
// ベクトルB
line(0, 0, B.x, B.y);
// ベクトルBを正規化
const Bn = B.normalize();
print(Bn.mag()); // 大きさは1
// ベクトルAと単位ベクトルとの内積
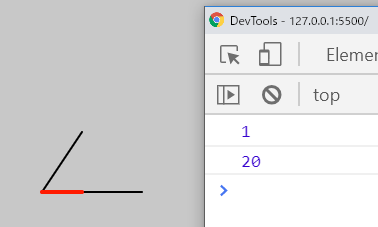
const dot = p5.Vector.dot(A, Bn);
print(dot); // 20
// dotの量を線で描く
stroke(255, 0, 0);
strokeWeight(2);
line(0, 0, dot, 0);
}
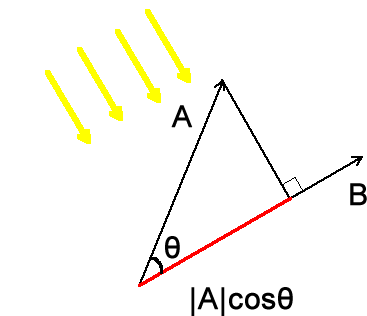
上図の赤色で示している部分は、ベクトルAの射影と呼ばれます。射影は、2つのベクトルの始点を合わせ、この始点から、一方のベクトルの終点からもう一方のベクトルに垂線を下したときの交点までの長さです。
射影は、下図に示すように、ベクトルBに垂直に、ベクトルAの上から光を当てたときにできるベクトルAの影と考えることができます。この長さは|A|cosθです。
AIにも応用される
上記「斜面に対する反射」サンプルには直接関係しませんが、内積はAIでも使われます。たとえば単語の意味をベクトルで表現し、単語が似ているかどうかを、ベクトルの内積で判断するのです。これについては「9_3:似ているか? 似ていないか? ml5.js JavaScript」で述べています。
サンプルコードを見ていく
では、内積に関する前置きはこの程度にして、サンプルコードを見ていきましょう。
サンプルを実行してしばらく観察すると分かりますが、このサンプルでは、流れ星のように見える円がキャンバスの上と左右で跳ね返り、下方向についてはグレーの面(ベース上面)で跳ね返ります。円がベース上面と当たったときには、ベース上面と垂直の方向に、一瞬線が描かれます。ベース上面は、円が上端に当たったときに角度が変わります。この、角度の変わる面に対する跳ね返りが、このサンプルのポイントで、この計算に内積が使われています。
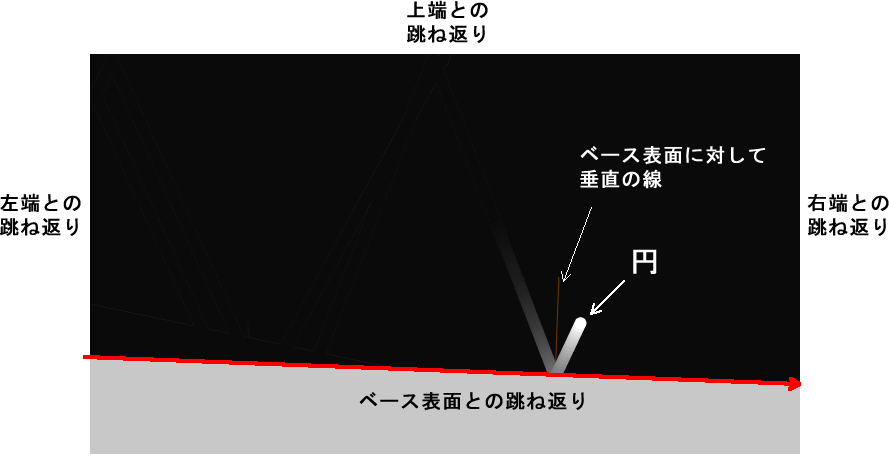
ベース上面
まずベース上面と呼んでいるものを見ていきます。
setup()関数では、base1とbase2という名前でベクトルが作成されています。
// ベース1とベース2のベクトルを作成
base1 = createVector(0, height - 150);
base2 = createVector(width, height);draw()関数では、次のコードでグレーの四辺形が作成されています。一見するとこれが跳ね返り対象の実体のように思えますが、これは見せかけです。ここでのポイントは、この四辺形の上の線が、(base1.x, base1.y)と(base2.x,base2.y)を結んでいることです。
quad(base1.x, base1.y, base2.x, base2.y, base2.x, height, 0, height);つづいて、次の1行で、base2からbase1を引いています。
let baseDelta = p5.Vector.sub(base2, base1);ここまで出てきたもの(base1、base2、四辺形、base2-base1)を、色違いの線で描画してみます。
let base1, base2;
function setup() {
createCanvas(710, 400);
base1 = createVector(0, height - 150);
base2 = createVector(width, height);
}
function draw() {
background(0);
// ベースを描画
fill(200);
noStroke();
quad(base1.x, base1.y, base2.x, base2.y, base2.x, height, 0, height);
// ベース1ベクトルを赤線で描画
stroke(255, 0, 0);
strokeWeight(5);
line(0, 0, base1.x, base1.y);
// ベース2ベクトルを緑線で描画
stroke(0, 255, 0);
line(0, 0, base2.x, base2.y);
// ベース2ベクトル - ベース1ベクトル を青線で描画
stroke(0, 0, 255);
let baseDelta = p5.Vector.sub(base2, base1);
line(0, 0, baseDelta.x, baseDelta.y);
}結果は次のようになります。
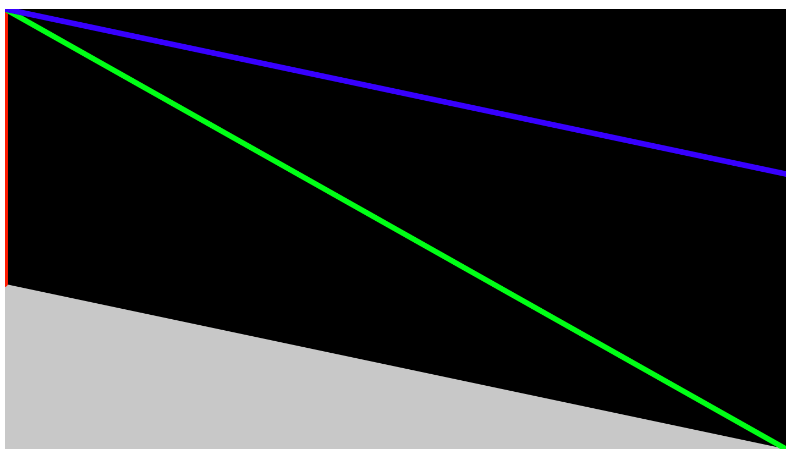
base2-base1というのはベクトルの引き算です。ベクトルの引き算は直感的に分かりづらいので、base2 + (-base1)、つまりbase2に、base1を逆にしたベクトルを足す、と考えるのも1つの手です。図にすると次のようになります。
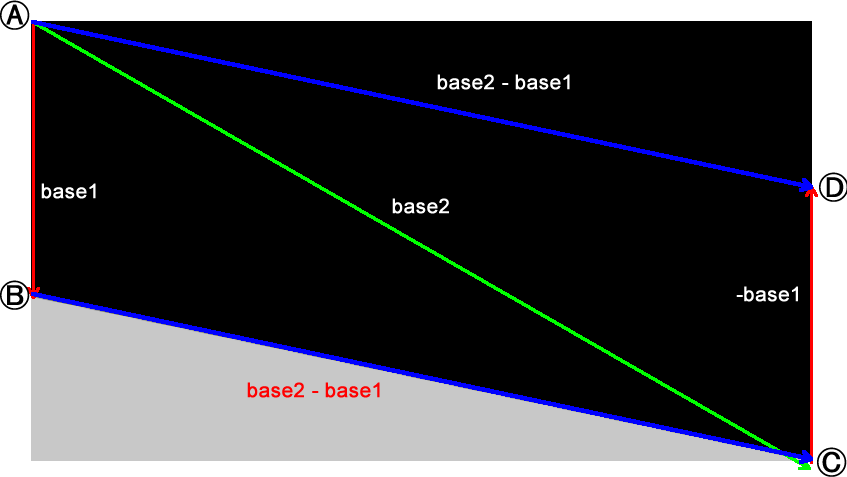
左端のbase1を逆にしたベクトル-base1の始点を、base2の終点に合わせます(ベクトルは自由に移動できます)。これがbase2-base1です。すると、青線で示した、始点が(0,0)、終点が(710,150)のベクトルになります。
そして、上図で示す点A、B、C、Dを結んで作られる四辺形は、辺ABと辺CDの長さが同じで平行なので、平行四辺形だと言えます(「平行四辺形になる条件」)。これは、辺ADが辺BCと並行ということで、つまりベクトルbase2-base1を移動すると、グレーの四辺形の上面にぴったり重なるということです。このベクトルbase2-base1、変数で言うとbaseDeltaが、円を跳ね返らせたいベース上面です。
ベース上面の法線ベクトル
コードではつづいて、baseDeltaを正規化し、その法線ベクトルを作成しています。
// ベース上面ベクトル
let baseDelta = p5.Vector.sub(base2, base1);
// 正規化(方向を残し、大きさを1にする)
baseDelta.normalize();
// ベース上面ベクトルの正規化された法線ベクトルを得る
let normal = createVector(-baseDelta.y, baseDelta.x);法線ベクトルは、「Vector Math Tutorial」ページに次のように説明されています。
法線ベクトルは、平面の向きを表す方向ベクトルの一種です。平面の法線は、平面の前面に垂直な外向きの方向を指します。たとえば、部屋の床の法線ベクトルは {0, 1, 0}になるでしょう(y成分が上を向いている)。法線はベクトルの反射や投影に使用されます。
法線ベクトルは平面に対して垂直なベクトルなので、平面に対して90度、時計回りの法線と、反時計回りの法線の2つが考えられます。点A(Ax,Ay)から点B(Bx,By)へのベクトルABに対する法線ベクトルは、次の方法で計算できます。
時計回りの法線:[Ay – By, Bx – Ax] 点Aが(0,0)の場合 => [-By, Bx]
反時計回りの法線:[By – Ay, Ax – Bx] 点Aが(0,0)の場合 => [By, -Bx]
点A(0,0)から点B(200,100)へのベクトルABで見てみると、時計回りの法線は、[0- 100, 200 – 0]なので[-100,200]です。AxとAyは0なので[-By, Bx]で計算できます。また、反時計回りの法線は、[100 - 0, 0 – 200]なので[100,-200]です。AxとAyは0なので[By, -Bx]で計算できます。
これは次のようなコードで確認できます。
function setup() {
createCanvas(400, 300);
background(200);
// 原点の上と左が見えるように座標システムを右下方向に移動
translate(120, 100);
// (Ax,Ay) => (Bx,By)
// (0,0)から(200,100)へのベクトル
const AB = createVector(200, 100);
// ベクトルAを赤線で描画
stroke(255, 0, 0);
line(0, 0, AB.x, AB.y);
// 時計回りの法線ベクトル
// [Ay - By, Bx - Ax]
// (0- 100), (200 - 0) = (-100,200)
// (-By, Bx)
const normal1 = createVector(-AB.y, AB.x);
// 法線を黄色の太線で描画
stroke(255, 255, 0);
strokeWeight(3);
line(0, 0, normal1.x, normal1.y);
// 反時計回りの法線ベクトル
// [By - Ay, Ax - Bx]
// (100 - 0), (0 - 200) = (100,-200)
// (By, -Bx)
const normal2 = createVector(AB.y, -AB.x);
// 法線を緑色の太線で描画
stroke(0, 255, 0);
line(0, 0, normal2.x, normal2.y);
}下図はこの説明図です。
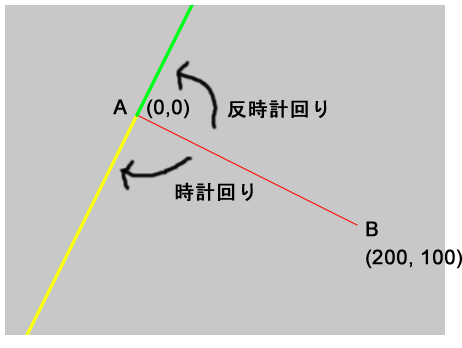
サンプルのコードでは、ベース上面ベクトルbaseDeltaのxとyを、createVector()関数に-baseDelta.y, baseDelta.xとして渡しているので、時計回りの法線ベクトルを作成していることになります。
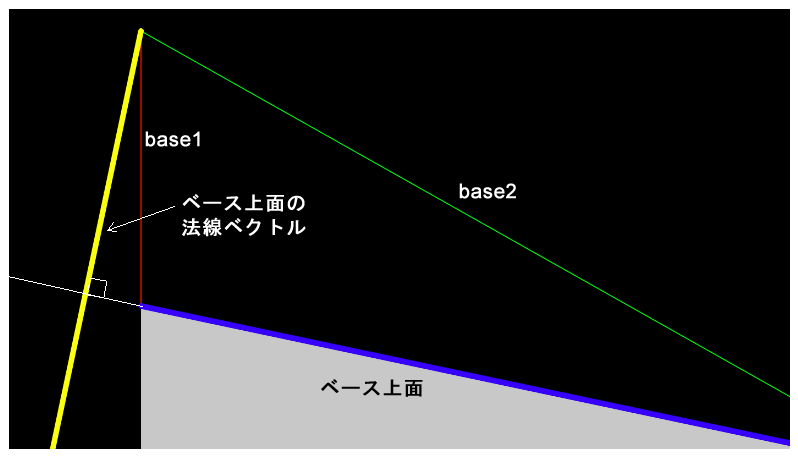
ベース上面までを描いたコードに、ベース上面の法線ベクトルを加えると、次のようになります。
let base1, base2;
function setup() {
createCanvas(710, 400);
base1 = createVector(0, height - 150);
base2 = createVector(width, height);
}
function draw() {
background(0);
// 原点の上と左が見えるように座標システムを右下方向に移動
translate(120, 20);
// ベースを描画
fill(200);
noStroke();
quad(base1.x, base1.y, base2.x, base2.y, base2.x, height, 0, height);
// ベース1ベクトルを赤線で描画
stroke(255, 0, 0);
strokeWeight(1);
line(0, 0, base1.x, base1.y);
// ベース2ベクトルを緑線で描画
stroke(0, 255, 0);
line(0, 0, base2.x, base2.y);
// ベース上面を青線で描画
stroke(0, 0, 255);
let baseDelta = p5.Vector.sub(base2, base1);
strokeWeight(5);
// 線は下に平行移動して描画
line(0, 250, baseDelta.x, baseDelta.y + 250);
// 正規化
baseDelta.normalize();
let normal = createVector(-baseDelta.y, baseDelta.x);
// print(normal.mag()) // 法線ベクトルの大きさは1
// 線で描画するので、視認しやすいように400倍する
let normalC = normal.copy().mult(400);
// 法線を黄色の線で描画
stroke(255, 255, 0);
strokeWeight(5);
line(0, 0, normalC.x, normalC.y);
}
ベース上面との衝突判定
ベース上面の法線ベクトルを作成し、変数normalに代入した行から少し下ると、次のifステートメントがあります。これは、円とベース上面との”衝突判定”を、内積を使って行おうとするコードです。
// ベースとの衝突を判定して処理する
if (p5.Vector.dot(normal, position) > intercept) {と言っても、円とベース上面が実際に重なるタイミングを調べるものではなく、2つの内積の計算の大小比較です。以降ではこれを見ていきます。
変数positionとinterceptはまだ設定していないので、これらを組み込みます。positionは円の位置を表すベクトルで、interceptはbase1とnormalとの内積です。
サンプルコードにしたがい、positionとinterceptを組み込んで、関係するベクトルを描画するコードは次のようになります。
let base1, base2;
// 移動するボールに関係する変数
let position;
let r = 6;
function setup() {
createCanvas(710, 400);
base1 = createVector(0, height - 150);
base2 = createVector(width, height);
// 円の位置を表すベクトル
position = createVector(width / 2, 0);
noLoop(); // draw()を1回だけ実行
}
function draw() {
background(0);
// 原点の上と左が見えるように座標システムを右下方向に移動
translate(120, 50);
fill(200);
noStroke();
quad(base1.x, base1.y, base2.x, base2.y, base2.x, height, 0, height);
stroke(255, 0, 0);
strokeWeight(1);
line(0, 0, base1.x, base1.y);
let baseDelta = p5.Vector.sub(base2, base1);
baseDelta.normalize();
let normal = createVector(-baseDelta.y, baseDelta.x);
let normalC = normal.copy().mult(400);
stroke(255, 255, 0);
strokeWeight(1);
line(0, 0, normalC.x, normalC.y);
// positionベクトルを青線で描画
stroke(0, 0, 255);
strokeWeight(1);
line(0, 0, position.x, position.y);
// positionベクトルの終点を白丸で描画
ellipse(position.x, position.y, r * 2, r * 2);
// ベース1と法線の内積
let intercept = p5.Vector.dot(base1, normal);
print(intercept);
// positionと法線の内積
let p = p5.Vector.dot(position, normal);
print(p);
}これを実行すると、base1とベース上面の法線ベクトルを示す線に加え、positionベクトルの線と、その終点を示す円が描画され、コンソールに2つの内積結果の数値が表示されます。positionはcreateVector(width / 2, 0)で作成しているので、キャンバスゼンターの上端に円が描かれ、そことキャンバスの原点を結ぶ線が描かれます。
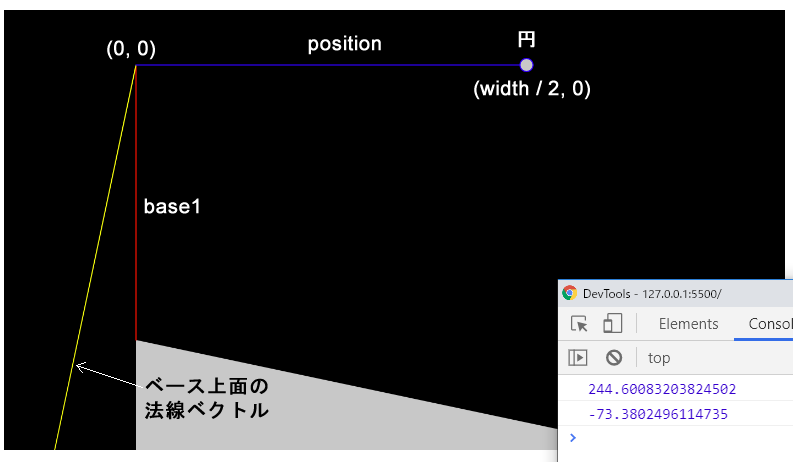
interceptはbase1と、ベース上面の法線ベクトルnormalとの内積で、変数pはpositionと、ベース上面の法線ベクトルnormalとの内積です。その値はそれぞれ、244.60…と-73.38…です。これが意味するものを図で考えてみましょう。
// ベース1と法線の内積
let intercept = p5.Vector.dot(base1, normal);
print(intercept); // 244.60...
// positionと法線の内積
let p = p5.Vector.dot(position, normal);
print(p); // -73.38...base1とpositionは通常のベクトルで、normalは正規化した単位ベクトルです。これらの内積には、前述した内積の使い道の「ベクトルAと単位ベクトルとの内積で、ベクトルAの、単位ベクトル方向への成分が分かる」が当てはまります。
base1とpositionの値が示すものを分かりやすくするため、normalの方向が水平になるように上図を回転させると、下図になります。
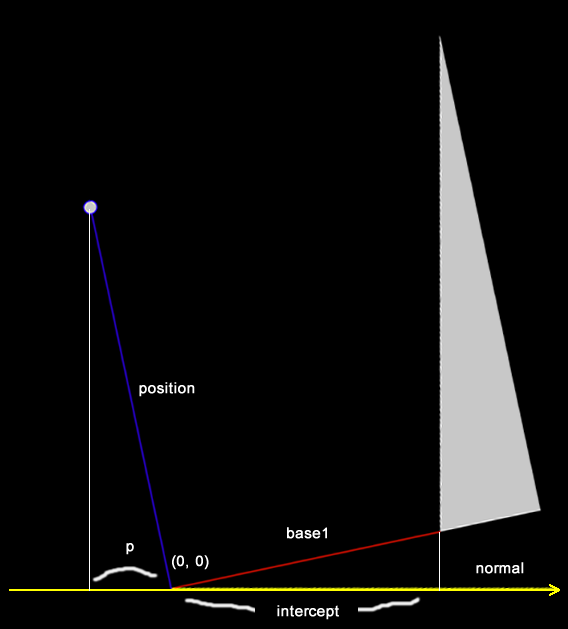
「ベクトルAと単位ベクトルとの内積で、ベクトルAの、単位ベクトル方向への成分が分かる」の図を見直すと直感的にお分かりかもしれませんが、interceptは、base1の、単位法線ベクトルnormalへの射影であり、その値は244.60…です。pは、positionの単位法線ベクトルnormalへの射影であり、その値は-73.38…です。前のifステートメントでは、これらの値の大小を比較していたのです。
*注意:上図ではnormalを長く表示していますが、normalは正規化された法線ベクトルなので、あくまでも大きさは1です。
// ベースとの衝突を判定して処理する
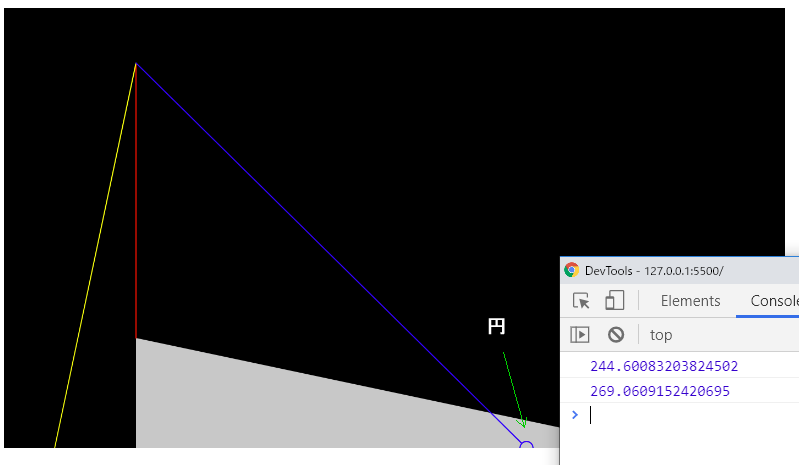
if (p5.Vector.dot(normal, position) > intercept) {今の場合、pの方がinterceptより小さいので、このifステートメントの条件には当てはまりません。しかしpositionをたとえばcreateVector(width / 2, 350)で作成すると、pの方が大きくなります。このとき円は、下図に示すように、ベース上面より下にあります。
そしてpositionをposition = createVector(width / 2, 325)で作成すると、円はベース上面の上に来て、pとinterceptの値が等しくなります。
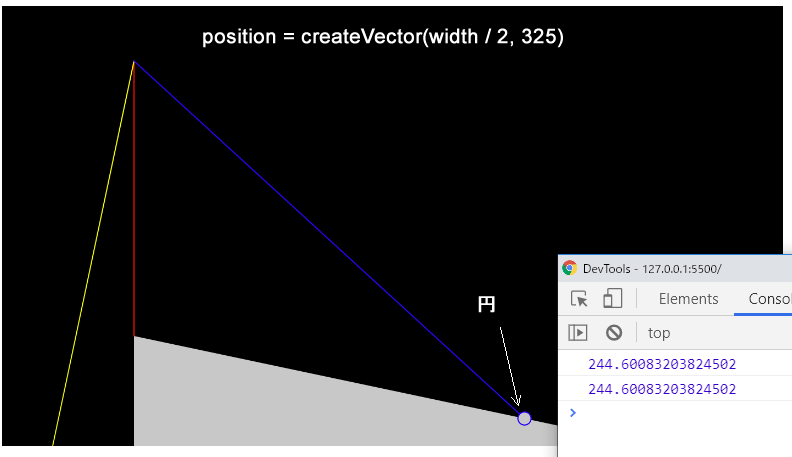
これは、pがinterceptより小さいときには、円はベース上面より上にあり、pがinterceptより大きいときには、円はベース上面より下にある、そしてpとinterceptが等しいときには、円はベース上面の上にある、ということなので、pとinterceptの大小比較によって、円とベース上面との衝突判定が行える、ということです。
衝突判定の方法が分かったら、次は円を実際に動かして、衝突に反応させる手順です。
反射ベクトル
p5.jsの「斜面に対する反射」サンプルの説明文に書かれている式(R = 2N(N・L)-L)は、ここで使います。Rは反射ベクトル、Nは法線ベクトル、Lは入射ベクトルです。
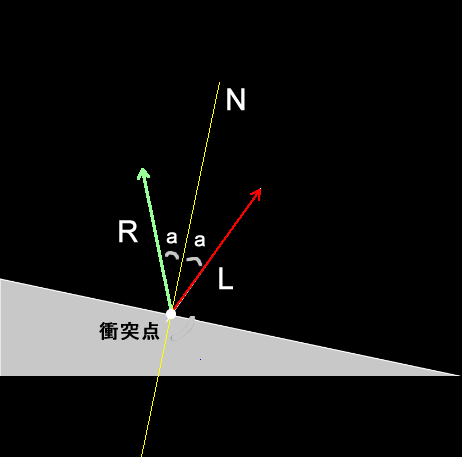
このサンプルで扱っている円の斜面に対する反射は、下図を想定しています。赤い矢印の方向から落ちてきたボールは、斜面に当たると、斜面の法線に対する、図のaと同じ角度で反射します。斜面であるベース上面は、円がキャンバス上端に当たるたびに角度が変わるので、円の反射の動作もそのたびに変える必要があります。
反射ベクトルを考える上でのポイントは、衝突点に入って来るベクトルの逆のベクトルを入射ベクトルとして扱うことです。下図で示す赤線のLで、ベクトルの矢印が衝突点の外を向いています。
衝突面に平行なベクトル
上記公式をそのまま当てはめて試行錯誤する手もあるでしょうが、コードの符号を無暗に変えて時間を過ごすより、きちんと理解した方が、後々応用が効くようになります。ただし反射ベクトルを理解するには、衝突面に平行なベクトルを理解する必要があるので、進む道はそう平坦ではありません。衝突面に平行なベクトルは今の場合、ベース上面に平行なベクトルです。下図はその説明図です。
下部のグレーの部分はベースで、円は衝突点でベース上面と衝突します。このときの衝突面に平行なベクトルは緑色の矢印です。衝突面に平行なベクトルを右上に移動し、始点をLの終点と合わせます。これをWとします。
下図を見ると、WはLを逆にした-LとaNを足すことで求められそうに思えます。
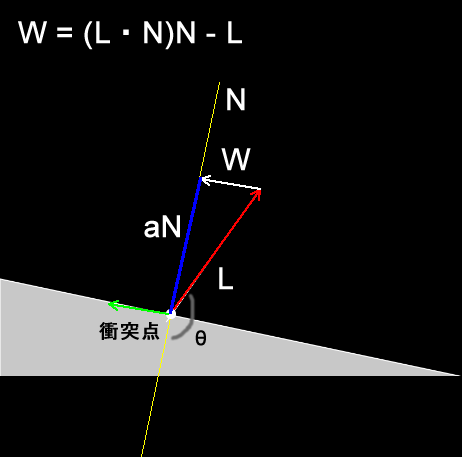
aはLと法線ベクトルNの内積です( a = L・N )。したがってWは、
W = -L + (L・N) * N で計算できることが分かります。
次のコードは、式W = -L + (L・N) * N を使って、衝突面に平行なベクトルに沿って円を移動させる例です。円の位置を表すベクトルはposition、移動速度はベクトルvelocityで表しています。
// ベース上面に沿って円が移動する
let base1, base2;
let position;
const r = 6;
// 円の移動速度
const speed = 3.5;
function setup() {
createCanvas(710, 400);
base1 = createVector(0, height - 150);
base2 = createVector(width, height);
// 円を、画面中央の上端でスタート
position = createVector(width / 2, 0);
// 円が下に落ちるためのベクトル
// サンプルではランダムに作成しているが、テストしやすいように確実に落下するベクトルにする。
velocity = createVector(-0.5, 0.7);
// ベクトルvelocityをspeed倍する
velocity.mult(speed);
}
function draw() {
background(0);
fill(200);
quad(base1.x, base1.y, base2.x, base2.y, base2.x, height, 0, height);
let baseDelta = p5.Vector.sub(base2, base1);
baseDelta.normalize();
let normal = createVector(-baseDelta.y, baseDelta.x);
let intercept = p5.Vector.dot(base1, normal);
// 円の位置(position.x, position.y)に描画
noStroke();
fill(255);
ellipse(position.x, position.y, r * 2, r * 2);
// 円の軌跡を線で描画
stroke(255)
line(width / 2, 0, position.x, position.y)
// 円を移動 => 位置は速度によって変化する
position.add(velocity);
// ベース上面に平行なベクトルWを求める
// W = (L・N)N - L
// 入射ベクトルは、velocityの逆ベクトル
// ベクトルに-1を掛けると、長さは変わらず向きが逆になる
let incidence = p5.Vector.mult(velocity, -1);
incidence.normalize();
// ベースとの衝突を調べ処理する
if (p5.Vector.dot(position, normal) > intercept) {
// 入射ベクトルと法線ベクトルの内積を求める
// a = L・N
let dot = incidence.dot(normal);
// W = aN - L
const Wx = dot * normal.x - incidence.x;
const Wy = dot * normal.y - incidence.y;
// velocityに適用 = ベース上面に平行なベクトル
velocity.set(Wx, Wy, 0);
// velocityをspeed倍する
velocity.mult(speed);
}
}このコードを実行すると、円が位置(width / 2, 0)から、velocityベクトルの方向にspeedの速さで落ちていきます(下図左)。そしてベース上面と衝突すると(下図中)、ベース上面に沿ってせりあがっていきます(下図右)。

反射ベクトル
反射ベクトルは下図に示す、トリッキーに思えるような方法で計算されます。つまりLの始点を衝突点に合わせ、それにaNを2回足す、という考え方です。
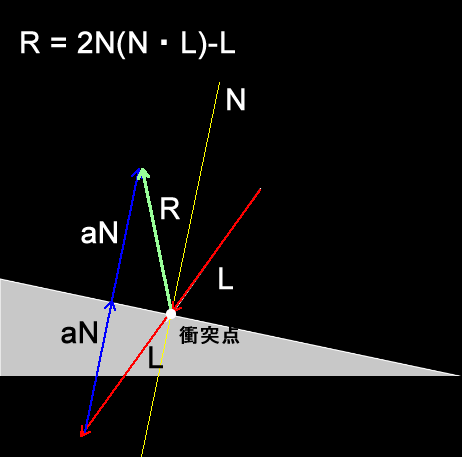
Rは-L + aN + aN なので、-L + 2aNです。aは前に求めた L・N なので、R = -L + 2*( L・N)*N となります。これは、前のWで求めた式に2を掛けるだけのものです。次のように変更するだけで、反射ベクトルが実装できます。
const Wx = dot * 2 * normal.x - incidence.x;
const Wy = dot * 2 * normal.y - incidence.y;リニア(線形)
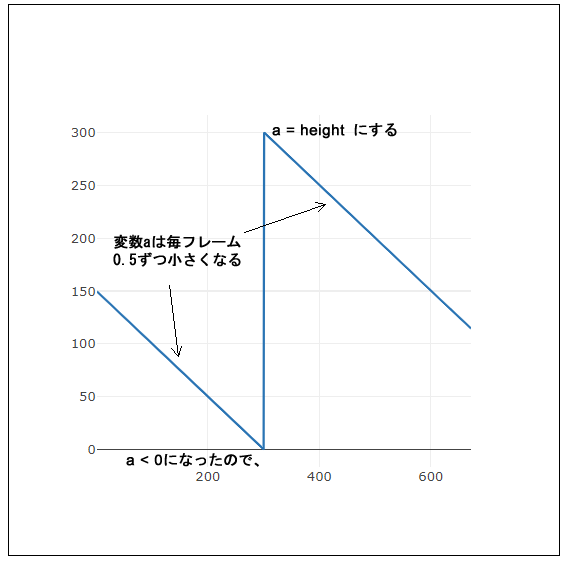
変数を値を変えることで、移動する線を作成します。線がキャンバス上端を超えると、変数はheightに設定されます。これにより、線はキャンバス下端に戻ります。
let a;
function setup() {
canvas = createCanvas(400, 300);
stroke(255);
// 変数aの初期値は高さの半分
a = height / 2;
}
function draw() {
background(51);
// 点(0,a)から(400,a)まで、毎フレーム、横線を描く
// aは0.5ずつ小さくなるので、横線が上に移動するアニメーションになる。
line(0, a, width, a);
// aを0.5だけ小さくする
a = a - 0.5;
// aがマイナスになったら、300に戻す => 横線のアニメーションがキャンバス下端から再スタート
if (a < 0) {
a = height;
}
}解説
リニアとは線形、直線を意味します。毎フレーム、同じ速度で移動するので、物理で言う等速直線運動になります。直線の意味は、下図のように、横軸にframeCount、縦軸に変数aの値を取るグラフを作成すると、容易に理解できます。
跳ね返り
シェイプがキャンバスの端に当たると、方向が反転します。
const rad = 60; // シェイプの幅
let xpos, ypos; // シェイプの開始位置
const xspeed = 2.8; // シェイプのスピード
const yspeed = 2.2; // シェイプのスピード
let xdirection = 1; // 左から右
let ydirection = 1; // 上から下
function setup() {
createCanvas(720, 400);
noStroke();
// フレームレートをデフォルトの半分にする
frameRate(30);
// ellipse()の第1と第2引数を円の中心に、第3と第4を幅と高さとして解釈する
ellipseMode(RADIUS);
// シェイプの開始位置をキャンバスセンターにする
xpos = width / 2;
ypos = height / 2;
}
function draw() {
background(102);
// 論理を更新 => 変数を更新
update();
// シェイプを描画する
// 点(xpos, ypos)を中心に半径radの円を描く
ellipse(xpos, ypos, rad, rad);
}
function update() {
// シェイプの位置を更新する
xpos = xpos + xspeed * xdirection;
ypos = ypos + yspeed * ydirection;
// シェイプが画面の境界を超えたかどうかを調べる
// 超えている場合には、-1を掛けることで、向きを反転する
if (xpos > width - rad || xpos < rad) {
xdirection *= -1;
}
if (ypos > height - rad || ypos < rad) {
ydirection *= -1;
}
}解説
上下左右の境界との跳ね返りについては、「7_2:速度と方向 p5.js JavaScript」で詳しく述べています。
互いに跳ね返る泡
キース・ピータースのコードにもとづく。複数オブジェクトの衝突。
sketch.js
const numBalls = 13; // ボールの数
const spring = 0.05; // ばね係数
const gravity = 0.03; // 重力
const friction = -0.9; // まさつ係数
const balls = []; // Ballオブジェクトを入れて管理する配列
function setup() {
createCanvas(720, 400);
// numBalls回だけ繰り返す
for (let i = 0; i < numBalls; i++) {
// Ballオブジェクトを作成
balls[i] = new Ball(
random(width),
random(height),
random(30, 70),
i,
balls
);
}
noStroke();
}
function draw() {
background(0);
// 配列要素を、与えられた関数で順に処理する
balls.forEach(ball => {
ball.collide();
ball.move();
ball.display();
});
}Ball.js
class Ball {
constructor(xin, yin, din, idin, oin) {
this.x = xin;
this.y = yin;
this.vx = 0;
this.vy = 0;
this.diameter = din;
this.id = idin;
this.others = oin;
}
collide() {
for (let i = this.id + 1; i < numBalls; i++) {
// console.log(others[i]);
let dx = this.others[i].x - this.x;
let dy = this.others[i].y - this.y;
let distance = sqrt(dx * dx + dy * dy);
let minDist = this.others[i].diameter / 2 + this.diameter / 2;
// console.log(distance);
//console.log(minDist);
if (distance < minDist) {
//console.log("2");
let angle = atan2(dy, dx);
let targetX = this.x + cos(angle) * minDist;
let targetY = this.y + sin(angle) * minDist;
let ax = (targetX - this.others[i].x) * spring;
let ay = (targetY - this.others[i].y) * spring;
this.vx -= ax;
this.vy -= ay;
this.others[i].vx += ax;
this.others[i].vy += ay;
}
}
}
move() {
this.vy += gravity;
this.x += this.vx;
this.y += this.vy;
if (this.x + this.diameter / 2 > width) {
this.x = width - this.diameter / 2;
this.vx *= friction;
}
else if (this.x - this.diameter / 2 < 0) {
this.x = this.diameter / 2;
this.vx *= friction;
}
if (this.y + this.diameter / 2 > height) {
this.y = height - this.diameter / 2;
this.vy *= friction;
}
else if (this.y - this.diameter / 2 < 0) {
this.y = this.diameter / 2;
this.vy *= friction;
}
}
display() {
ellipse(this.x, this.y, this.diameter, this.diameter);
}
}解説
このサンプルの大きな特徴は、ボールのオブジェクトが自分自身でほかのボールのオブジェクトとの衝突を判定し、互いに跳ね返り合う点です。
複数のオブジェクトを処理したい場合、複数のオブジェクトを配列に入れ、その配列をforループを使って処理する方法がよく取られますが、複数のオブジェクト同士の衝突の場合には、ただ配列を走査しただけでは、無用な計算が出てしまいます。つまり、AとBが衝突しているかどうかを調べることはBとAが衝突しているかどうかを調べることと同じなので、どちらか一方は必要ないわけです。
このサンプルではそれが実にうまい方法で処理されています。それはBallクラスのcollide()メソッド内の、次のforループにあります。
// numBalls - 自分のid番号より1大きい数の回数だけ繰り返す
// 自分自身に対する衝突処理は行わず、かつ重複した衝突処理も行わない
for (let i = this.id + 1; i < numBalls; i++) {
// this.othersは作成された全Ballオブジェクトを含む配列
// 確認用
if (this.id === 0) {
print('ball' + this.id + 'にとってのothers[i]は: ' + this.others[i].id);
}
// x方向での、処理対象と自分との差
const dx = this.others[i].x - this.x;
...this.idはBallオブジェクトのidで、そのオブジェクト固有の番号です。ball0、ball1、ball2のように考えることができます。numBallsはsketch.jsで定義される、作成するBallオブジェクトの個数です。そして、this.othersは、sketch.jsで作成したBallオブジェクト全部を入れた配列です。Ballオブジェクトはこの配列を全部のオブジェクトが持っています。
たとえばnumBallsを3にして、Ballオブジェクトを作成すると、Ballオブジェクトのothers配列は[ball0, ball1, ball2]となります。そしてcollide()メソッドが呼び出されるときには、次のforループが実行されます。変数iはthis.idに1を足した値で初期化されるので、ループの実行回数はオブジェクトのthis.idの値によって変わります。
for (let i = this.id + 1; i < 3; i++) {具体的に見ていくと、
ball0のcollide()では、i=0+1=1 なので、i=1とi=2の2回、繰り返しが実行され、
ball1のcollide()では、i=1+1=2 なので、i=2の1回、繰り返しが実行され、
ball3のcollide()では、i=2+1=3 なので、繰り返しはなし、
となります。
以降のコードではこのiがthis.others配列のインデックスとして使用されるので、たとえばi=1なら[ball0,ball1,ball2]のball1が、i=2ならball2が参照されることになります。
次のようなコードを挿入すると、たとえばball0にとっての対象が明確になります。
if (this.id === 0) {
print('ball' + this.id + 'にとってのothers[i]は: ' + this.others[i].id);
}つまりこのforループの条件は、numBalls – 自分のid番号より1大きい数の回数だけ繰り返すことで、 自分自身に対する衝突処理は行わず、かつ重複した衝突処理も行わないことを可能にしているというわけです。
以下に永井が手を加えたsketch.jsとBall.jsのコードとその実行結果を示します。コードには細かな説明もつけているので、特にBallオブジェクト同士が互いに離れる部分に注目して読んでみてください。
sketch.js
const numBalls = 5; // ボールの数
const spring = 0.05; // ばね係数
const gravity = 0.03; // 重力
const friction = -0.9; // まさつ係数
const balls = []; // Ballオブジェクトを入れて管理する配列
function setup() {
createCanvas(720, 400);
// numBalls回だけ繰り返す
for (let i = 0; i < numBalls; i++) {
// Ballオブジェクトを作成
balls[i] = new Ball(
random(width),
random(height),
random(30, 70),
i,
balls
);
}
noStroke();
}
function draw() {
background(0);
// 配列要素を、与えられた関数で順に処理する
balls.forEach(ball => {
ball.collide();
ball.move();
ball.display();
});
// forループの方が分かりやすい
/*
for (let i = 0; i < balls.length; i++) {
const ball = balls[i];
ball.collide();
ball.move();
ball.display();
}
*/
if (frameCount > 6) {
// noLoop();
}
}Ball.js
// Ballクラス
class Ball {
constructor(xin, yin, din, idin, oin) {
this.x = xin; // 自分のx位置
this.y = yin; // 自分のy位置
this.vx = 0; // 自分の水平方向の速度
this.vy = 0; // 自分の垂直方向の速度
this.diameter = din; // 自分の直径
this.id = idin; // 自分のID番号
this.others = oin; // Ballオブジェクトを入れた配列
// 自分の色
this.color = color(random(0, 255), random(0, 255), random(0, 255));
// 確認用
this.hitting = false;
this.hittingInfo = {};
}
// ボール同士の衝突を処理する
collide() {
// numBalls - 自分のid番号より1大きい数の回数だけ繰り返す
// 自分自身に対する衝突処理は行わず、かつ重複した衝突処理も行わない
for (let i = this.id + 1; i < numBalls; i++) {
// this.othersは作成された全Ballオブジェクトを含む配列
// 確認用
if (this.id === 0) {
print('ball' + this.id + 'にとってのothers[i]は: ' + this.others[i].id);
}
// x方向での、処理対象と自分との差
const dx = this.others[i].x - this.x;
// y方向での、処理対象と自分との差
const dy = this.others[i].y - this.y;
// 自分と処理対象との距離を算出
const distance = sqrt(dx * dx + dy * dy);
// 自分とその処理対象が接触状態にあるときの距離
// => 衝突状態でなくするための最小距離
const minDist = this.others[i].diameter / 2 + this.diameter / 2;
// 今の距離が最小距離より小さいなら => 衝突状態にある
if (distance < minDist) {
// 確認用
print('衝突');
this.hitting = true;
// 衝突対象との角度を計算
let angle = atan2(dy, dx);
// 自分の位置から衝突状態でなくする最短のxとy位置 => この位置まで離したい
const targetX = this.x + cos(angle) * minDist;
const targetY = this.y + sin(angle) * minDist;
// 確認用
this.hittingInfo.targetX = targetX;
this.hittingInfo.targetY = targetY;
// 加速度を設定
// 離したい最短の位置から衝突対象の位置の差にばね係数を掛けたものを加速度とする
// これはイージングの考えを応用した使い方
let ax = (targetX - this.others[i].x) * spring;
let ay = (targetY - this.others[i].y) * spring;
// 加速度を自分と衝突対象に適用 =>互いに離れる
this.vx -= ax;
this.vy -= ay;
this.others[i].vx += ax;
this.others[i].vy += ay;
}
}
}
// ボールの移動
move() {
// 重力によって落下
this.vy += gravity;
// 位置は速度によって変化する
this.x += this.vx;
this.y += this.vy;
// キャンバスの上下左右の端との跳ね返り
// frictionはこのクラスでなく、sketch.jsで定義している変数
// -0.9の場合には、方向が反転して、速度が10%遅くなる
if (this.x + this.diameter / 2 > width) {
this.x = width - this.diameter / 2;
this.vx *= friction;
}
else if (this.x - this.diameter / 2 < 0) {
this.x = this.diameter / 2;
this.vx *= friction;
}
if (this.y + this.diameter / 2 > height) {
this.y = height - this.diameter / 2;
this.vy *= friction;
}
else if (this.y - this.diameter / 2 < 0) {
this.y = this.diameter / 2;
this.vy *= friction;
}
}
// 自分の色と直径で円を描く
display() {
fill(this.color);
ellipse(this.x, this.y, this.diameter, this.diameter);
// 確認用
// 自分のID番号を表示
fill(0);
text(this.id, this.x, this.y);
// 衝突相手を離したい位置まで線を引く
if (this.hitting) {
stroke(255);
strokeWeight(2);
line(this.x, this.y, this.hittingInfo.targetX, this.hittingInfo.targetY);
noStroke();
}
}
}モーフィング
シェイプの頂点を一方からもう一方へ補間をかけることことで、別の形状に変化させます
// このサンプルでは、円と正方形が同じ数の頂点を持つことを前提とする。
// これは、頂点(実際はベクトル)を保持する配列の長さは同じになるということ。
// 円用のベクトルを保持する配列
let circle = [];
// 正方形用のベクトルを保持する配列
let square = [];
// 描画に使用する頂点を保持する配列
let morph = [];
// 円にモーフィングするか正方形にモーフィングするか
// falseなら正方形にモーフィングする
let state = false;
function setup() {
createCanvas(720, 400);
// 中心から外に向かうベクトルを使って円を作成する
for (let angle = 0; angle < 360; angle += 9) {
// 正方形のパスに合わせる必要があるので、0から開始していないことに注意
// squareには、正方形の上辺左のベクトルから入れていくので、それに対応させるのが-135度
let v = p5.Vector.fromAngle(radians(angle - 135));
v.mult(100);
circle.push(v);
// ついでにmorph配列も、空のp5.Vectorオブジェクト(x,y,zが0)で埋めておく
// 要素数はcircle配列と同数
morph.push(createVector());
}
/// 正方形は直線に沿ったたくさんの頂点
// 正方形の上辺
for (let x = -50; x < 50; x += 10) {
square.push(createVector(x, -50));
}
/// 右辺
for (let y = -50; y < 50; y += 10) {
square.push(createVector(50, y));
}
// 下辺
for (let x = 50; x > -50; x -= 10) {
square.push(createVector(x, 50));
}
// 左辺
for (let y = 50; y > -50; y -= 10) {
square.push(createVector(-50, y));
}
}
function draw() {
background(51);
// 頂点がターゲットからどれだけ離れているかを保持する
let totalDistance = 0;
// circleまたはsquareの各ベクトルを取り出し、morphの各ベクトルをそれに近づける
for (let i = 0; i < circle.length; i++) {
let v1;
// 円への補間か正方形への補間か?
if (state) {
v1 = circle[i];
}
else {
v1 = square[i];
}
// v1に対応するベクトルを特定
let v2 = morph[i];
// ターゲット(v1)に近づける
v2.lerp(v1, 0.1);
/// 2点間の距離を積算 => 小さいほどv2はv1は似ていると考えられる
totalDistance += p5.Vector.dist(v1, v2);
}
// v2がv1に十分近づいたと見なせるなら、シェイプを切り替える
if (totalDistance < 0.1) {
state = !state;
}
// キャンバスセンターを基準に描画する
translate(width / 2, height / 2);
strokeWeight(4);
// すべての頂点から成る多角形を描画 => 実際に描画するのは40角形
beginShape();
noFill();
stroke(255);
morph.forEach(v => {
vertex(v.x, v.y);
});
endShape(CLOSE);
}解説
モーフィング(morphing)とは、「IT用語辞典 e-Words」によると、「コンピュータグラフィックスによる映像手法の一つで、ある画像や形状から別のイメージへ滑らかに変化させること。変形、(生物の)変態を意味する “metamorphosis” から派生した語とされる」とあります。下図は馬と象の形状を行き来するモーフィングGIFアニメーションの例です。

フリーで入手できるInkscapeは、図形を計算で作成するベクタータイプの描画アプリケーションなので、モーフィングが容易に実現できます。下図は円と星型シェイプに[補間]機能を適用した例です(参考:「Inkscape tutorial: Interpolate」)。

また、同じように見えるモーフィング効果はCSSを使っても、ブラウザ上で表現できます。下の四角形にマウスカーソルを重ねると、モーフィングして円に変化し、どかすと四角形に戻ります。
こういったモーフィングを、p5.jsの機能で実現しようというのがこのサンプルです。複雑な形状をコードから作成するのは相当面倒ですが、計算から作り出せる単純な形状同士のモーフィングなら、何とかなります。
モーフィングには、変化前と変化後の、図形を表す頂点の数を変えないという大前提があります。モーフィングは計算によって行われるので、頂点の数が変わってしまうと、矛盾が生じるからです。ベクター描画ツールの中には、これを自動的に補ってくれるものがありますが、p5.jsにはそんな機能はありません。
このサンプルでは、次の手順でモーフィングを実現します。
- 変化前の図形の頂点を表すp5.Vectorオブジェクトを作成し、専用の配列circleとsquareに入れる
- モーフィングの描画に使用する配列morphを、circleとsquareの要素数と同数で作成する
- circleまたはsquareから頂点情報を順番に取り出し、その頂点に、同じインデックスにあるmorph要素の頂点を近づける(補間)
- 前の時点より少し変化前の図形に近づいたmorphの頂点情報を使って、図形を描画する
円と正方形の頂点情報の作成
これは上記手順の1に当たります。円と正方形の頂点情報を、p5.Vectorオブジェクトとして作成し、circleとsquareに配列に入れます。
サンプルコードでは、これをsetup()関数内の次のforループで行っています。
for (let angle = 0; angle < 360; angle += 9) {
let v = p5.Vector.fromAngle(radians(angle - 135));
v.mult(100);
circle.push(v);
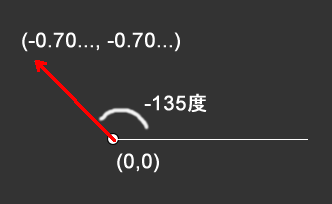
}p5.Vector.fromAngle()は与えられたラジアン単位の角度からベクトル(p5.Vectorオブジェクト)を作成するメソッドで、変数angleが0の初回の繰り返しでは、-135度のベクトルが作成されます。fromAngle(radians(angle – 135)が返す値を代入した変数vを出力してみると分かりますが、このベクトルvは(0, 0)から(-0.70…, -0.70…)を指すベクトルです。-135度というのは下図に示す角度です。
こうしたベクトルが、angle=0 から9刻みで40回(360/9)繰り返され作成され、100倍されて、作成順にcircle配列に追加されます。ではこの40のベクトルを線で描いてみましょう。
function setup() {
createCanvas(720, 400);
background(51);
// (0,0)の右上にあたる部分も見えるように、座標システムを右下に移動
translate(150, 150);
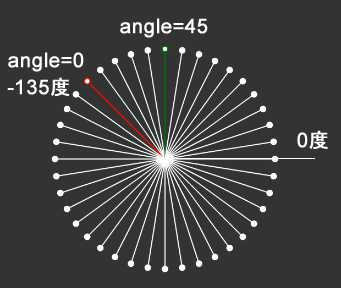
for (let angle = 0; angle < 360; angle += 9) {
let v = p5.Vector.fromAngle(radians(angle - 135));
v.mult(100);
circle.push(v);
// angleが0のときは線を赤に
if (angle === 0) {
stroke('red');
// angleが45のときは線を緑に
}
else if (angle === 45) {
stroke('green');
// それ以外の場合は線を白にする
}
else {
stroke('white');
}
// (0,0)を始点、v.x,v.yを終点とするベクトルを線で描く
line(0, 0, v.x, v.y);
// ベクトルの終点を小さな円で描く
ellipse(v.x, v.y, 5);
}
}これを実行すると、下図の結果が得られます。ベクトルを表す線は、angle=0の赤線からスタートし、(0,0)を中心に時計回りに進んで40本描かれます。またベクトルの終点を表す小さな白円は円状に並びます。配列circleには、こうしたベクトルが順番に入っていきます。circleの最初の要素は、-135度のベクトルです。
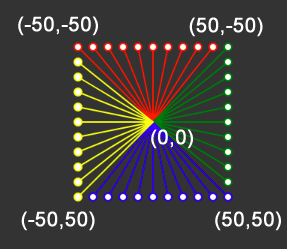
つづいて、配列squareに追加されるベクトルも線で描いてみましょう。次のコードでは、辺ごとに線の色を変えています。
stroke('red');
for (let x = -50; x < 50; x += 10) {
const topV = createVector(x, -50);
line(0, 0, topV.x, topV.y);
ellipse(topV.x, topV.y, 5);
square.push(topV);
}
// 右辺
stroke('green');
for (let y = -50; y < 50; y += 10) {
const rightV = createVector(50, y);
line(0, 0, rightV.x, rightV.y);
ellipse(rightV.x, rightV.y, 5);
square.push(rightV);
}
// 下辺
stroke('blue');
for (let x = 50; x > -50; x -= 10) {
const bottomV = createVector(x, 50);
line(0, 0, bottomV.x, bottomV.y);
ellipse(bottomV.x, bottomV.y, 5);
square.push(bottomV);
}
// 左辺
stroke('yellow');
for (let y = 50; y > -50; y -= 10) {
const leftV = createVector(-50, y);
line(0, 0, leftV.x, leftV.y);
ellipse(leftV.x, leftV.y, 5);
square.push(leftV);
}下図はこの実行結果です。ここで描かれる線は、(0,0)から外に向けて放射状に進み、ベクトルの終点に当たる白い円が正方形に並びます。線の数は合計で40本です。配列squareにはこうしたベクトルが入れられます。その最初の要素は、上辺の一番左を指すベクトルです。
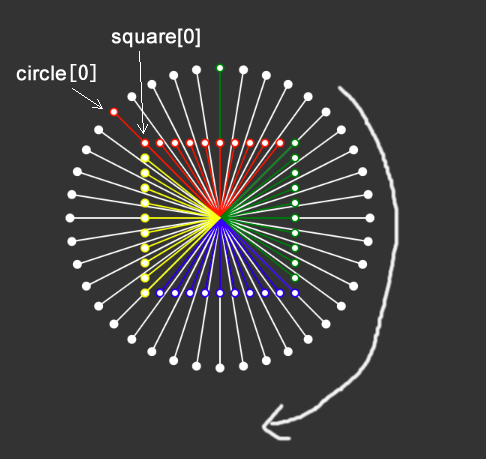
下図は前の円のベクトルと合わせて描画した結果です。これを見ると、circleの最初のベクトルとsquareの最初のベクトルはぴったり重なっている(向きが同じ)ことが分かります。(0,0)を中心としたときの正方形の左上隅は、(0,0)から見て、反時計回りに135度の方向にあります。circleに入れるベクトルの作成に使用した-135は、circleの最初のベクトルを、squareの正方形の左上隅に重ねるためだったのです。
最初を合わせると、配列の要素数はどちらも40で、均等の変化で円と正方形を描くので、同じインデックス番号の要素同士を対応させることができます。
morph配列にcircleの要素数と同数の要素を入れる
これは上記手順の2に当たります。circleにベクトルを追加するforループ内で、次のコードを実行すると、circleの要素数と同数のp5.Vectorオブジェクトをmorphに入れることができます。createVector()関数に引数を指定しないと、x,y,zが0のp5.Vectorオブジェクトが返されます。
// ついでにmorph配列も、空のp5.Vectorオブジェクト(x,y,zが0)で埋めておく
// 要素数はcircle配列と同数
morph.push(createVector());morph配列のベクトルを、circleかsquare配列のベクトルに近づける
これは前の手順3に当たります。ベクトルを別のベクトルに近づけるというのは、”似せる”と言い換えることもできます。この作業はp5.Vectorのlerp()メソッドが行います。
次の例では、(0,0)を指すベクトルv1を、(100,100)を指すv2に、”半分だけ似せ”ます。するとv1は(50,50)を指すベクトルに変化します。
let v1 = createVector(0, 0);
let v2 = createVector(100, 100);
// v1をv2に、0.5(=半分)近づける
v1.lerp(v2, 0.5);
print(v1); // [x,y] = [50,50]
lerp()メソッドの第2引数には、似せたい程度を0から1の間で指定します。たとえば0.1ではあまり似ませんが、0.9を指定するとよく似たベクトルに変わります。しかし0.1といった小さな値でも、それを繰り返すうち、次第に似てきます。この少しずつ似てくる変化がモーフィングを生み出します。
setup()関数で作成したcircleとsquare、morph配列を、次のdraw()関数で操作すると、モーフィングが描画されます。
function draw() {
background(51);
// 頂点がターゲットからどれだけ離れているかを保持する
let totalDistance = 0;
// circleまたはsquareの各ベクトルを取り出し、morphの各ベクトルをそれに近づける
for (let i = 0; i < circle.length; i++) {
let v1;
// 円への補間か正方形への補間か?
if (state) {
v1 = circle[i];
} else {
v1 = square[i];
}
// v1に対応するベクトルを特定
let v2 = morph[i];
// v2をv1に少し近づける
v2.lerp(v1, 0.1);
// 2点間の距離を積算 => 小さいほどv2はv1は似ていると考えられる
totalDistance += p5.Vector.dist(v1, v2);
}
// v2がv1に十分近づいたと見なせるなら、シェイプを切り替える
if (totalDistance < 0.1) {
state = !state;
}
// キャンバスセンターを基準に描画する
translate(width / 2, height / 2);
strokeWeight(4);
// すべての頂点から成る多角形を描画 => 実際に描画するのは40角形
beginShape();
morph.forEach(v => {
vertex(v.x, v.y);
});
endShape(CLOSE);
}p5.Vector.lerp()メソッドは、ターゲットに少しずつ近づくが決して到達することはない、という意味でイージングの手法と同じです(イージングについては「4_3:応答:イージングの導入 p5.js JavaScript」を参照)。ということは、十分に似ている形状に近づいたと言えるタイミングを見つけて、lerp()メソッドを停める必要があります。
このタイミングの目安としているのが変数totalDistanceです。totalDistanceには、v1とv2の終点を点と見立てた2点間の距離の積算値が入ります。2点間の距離は今の場合似ていなさを表すので、これが小さいほどv2はv1に似ていると考えられます。
totalDistance += p5.Vector.dist(v1, v2);十分に似ている形状に近づいたと見なすタイミングは次のif条件が握っています。totalDistanceが0.1より小さくなると、変数stateを反転させるのです。これにより、lerp()メソッドを停めるのではなく、モーフィング対象の図形が自動的に切り替わります
// v2がv1に十分近づいたと見なせるなら、シェイプを切り替える
if (totalDistance < 0.1) {
state = !state;
}frameCountをX軸に、totalDistanceの値をY軸にしてグラフを描画すると、totalDistanceの値が小さくなっていくのが分かります。そして0.1より小さくなったときに跳ね上がります。これはモーフィング対象の図形が切り替わり、似ていなくなったことを表しています。
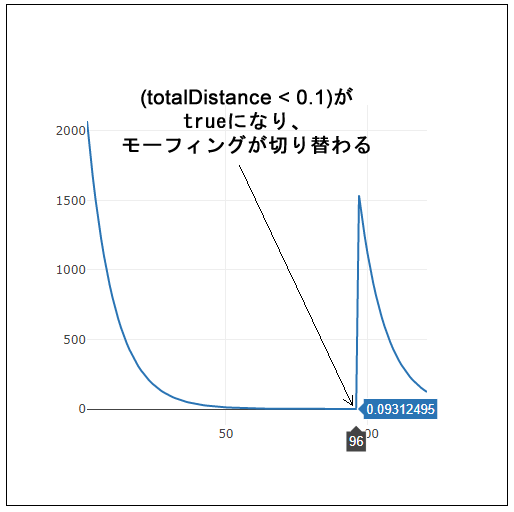
モーフィングの描画
モーフィングする図形を実際に描くのは次のコードです(手順4)。ベクトルの終点に当たるx値とy値をvertex()関数に渡してその位置に頂点を作成します。これをbeginShape()とendShape(CLOSE)で囲むと、頂点が結ばれて多角形が描画できます。頂点は40個作成されるので、円のように見えても実際は40角形が描かれていることになります。
beginShape();
morph.forEach(v => {
vertex(v.x, v.y);
});
endShape(CLOSE);vertex()とbeginShape()、endShape()関数については「2_7:p5.js シェイプを手作りする」で述べています。
リファレンスメモ
p5.Vector.fromAngle()
説明
新しい2Dベクトルを角度から作成する。
シンタックス
p5.Vector.fromAngle(angle, [length])
パラメータ
angle 数値:希望する角度、ラジアン単位(angleModeの影響は受けない)
length 数値:新しいベクトルの長さ(デフォルトは1) オプション
戻り
p5.Vector: 新しいp5.Vectorオブジェクト
* p5.Vector.fromAngles()という似た名前のメソッドもあるので注意。
p5.Vector.lerp()
説明
ベクトルを別のベクトルに線形補間する。
シンタックス
lerp(x, y, z, amt)
lerp(v, amt)
p5.Vector.lerp(v1, v2, amt, target)
p5.Vector.lerp(v1, v2, amt)
パラメータ
x 数値: x成分
y 数値: y成分
z 数値: z成分
amt 数値: 補間の量で、0.0(古いベクトル)と1.0(新しいベクトル)の間の値。0.9は新しいベクトルに非常に近く、0.5は古いベクトルと新しいベクトルの中間。
v p5.Vector: 補間するp5.Vector
v1 p5.Vector:
v2 p5.Vector:
target p5.Vector: 未定義の場合、新しいベクトルが作成される
*p5.Vectorのメソッドでない、同名のlerp()関数も存在するので注意。lerp()関数については「8:数学(Math)」の「線形補間」を参照。
曲線上を移動する
このサンプルでは、円が曲線 y = x^4 に沿って移動します。円の移動先はキャンバスのクリックで指定できます。
let beginX = 20.0; // 開始のx座標
let beginY = 10.0; // 開始のy座標
let endX = 570.0; // 終了のx座標
let endY = 320.0; // 終了のy座標
let distX; // X軸方向の移動距離
let distY; // X軸方向の移動距離
let exponent = 4; // 曲線を決める指数
let x = 0.0; // 現在のx座標
let y = 0.0; // 現在のy座標
const step = 0.01; // パスに沿った刻みの大きさ
let pct = 0.0; // 移動したパーセント(0.0 to 1.0)
function setup() {
createCanvas(720, 400);
noStroke();
distX = endX - beginX;
distY = endY - beginY;
}
function draw() {
// 円をにじませる効果
fill(0, 2);
rect(0, 0, width, height);
pct += step; // pctは0.01(1%)ずつ大きくなる
if (pct < 1.0) {
// 終わりに急なカーブを描いて近づく
x = beginX + pct * distX;
y = beginY + pow(pct, exponent) * distY;
}
fill(255);
ellipse(x, y, 20, 20);
}
// pctを0に戻してリセット
function mousePressed() {
pct = 0.0;
beginX = x;
beginY = y;
endX = mouseX;
endY = mouseY;
distX = endX - beginX;
distY = endY - beginY;
}解説
このサンプルで最も興味を引かれるのは、円が y=x^4(xの4乗)の曲線上を移動するということで、最初に分からないと思うのは、y=x^4 はどんな曲線なのか? ということです。
sketch.jsにplotly.jsライブラリを組み込むと、次のコードでy=x^4のグラフが描画できます。
// y = x^4 のグラフ
let pct = 0;
const step = 0.01;
function setup() {
}
function draw() {
plot(pct, pow(pct, 4));
pct += step;
// y値は急な曲線を描いて大きくなる
if (pct > 0.1) {
noLoop();
}
}下図は実行結果です。これを見ると、初めは穏やかに変化しますが、後になるほど急激に増加していることが分かります。これは、頭の中で想像しても容易に分かる特徴です。xが0.01や0.02といった小さな値のときはyも小さな値ですが、xが1を超えるとyはどんどん大きくなります。
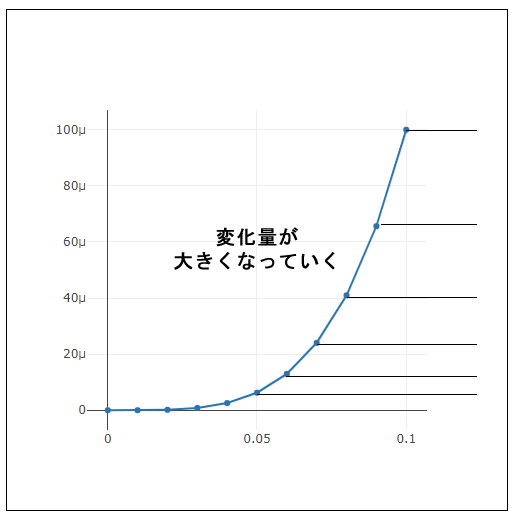
メモ
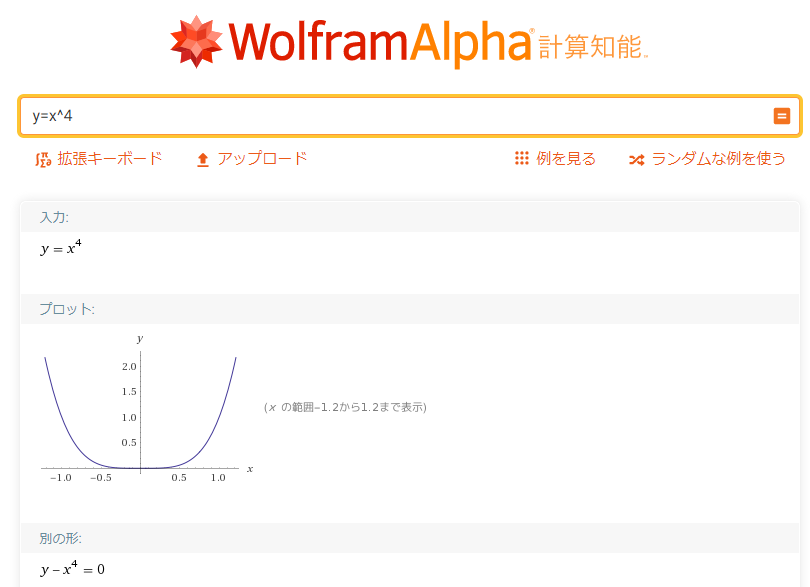
どんなグラフになるか確認したいだけなら、「WalframAlpha」計算知能ページが便利です。関数を入力するだけでグラフを描画してくれます。
円をy=x^4の曲がり具合で動かしているのは、draw()関数にある次の2行です。
x = beginX + pct * distX;
y = beginY + pow(pct, exponent) * distY;draw()関数の1回めを手計算してみると、beginX=20、pct=0, distX=570-20なので、x = 20 + 0*550 = 20 です。2回めは、20 + 0.01*550 = 20 + 5.5 = 25.5で、3回めは、20 + 0.02*550 = 20 + 11 = 31 です。つまりxは、draw()が呼び出されるたびに、5.5ずつ大きくなっていきます。方程式で書くとy = 550x + 20、グラフにするとの直線になります。
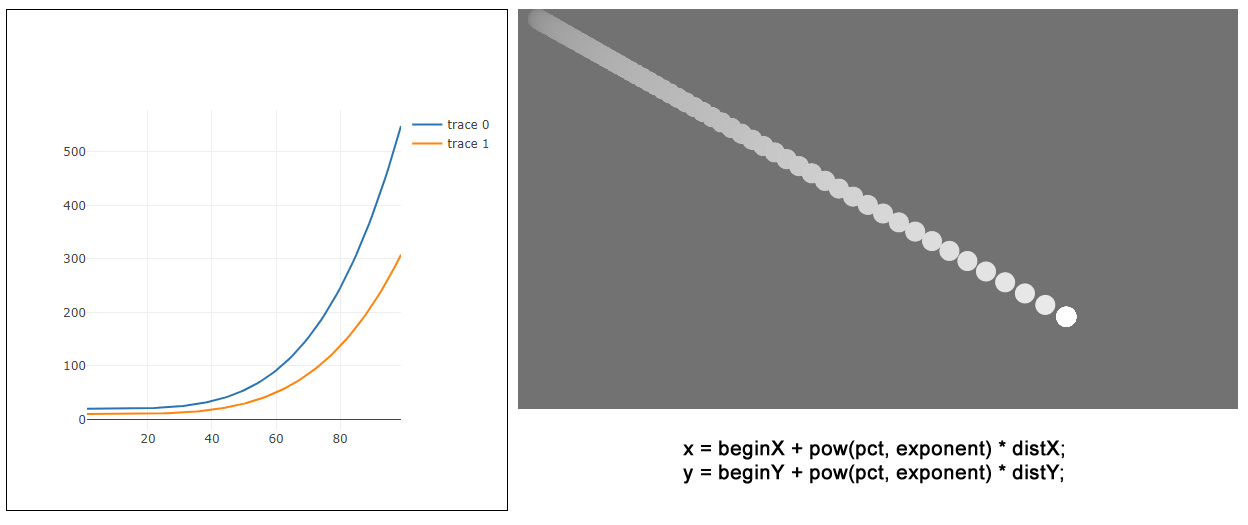
一方yは、20 + pct^4*550 なので、方程式で書くとy = 550x^4 + 20、グラフにすると曲線になります。下図はframeCountを横軸に、x = beginX + pct * distX と y = beginY + pow(pct, exponent) * distY を1つにしたグラフです。サンプルの円はこのxとyを自分の位置として移動するのです。
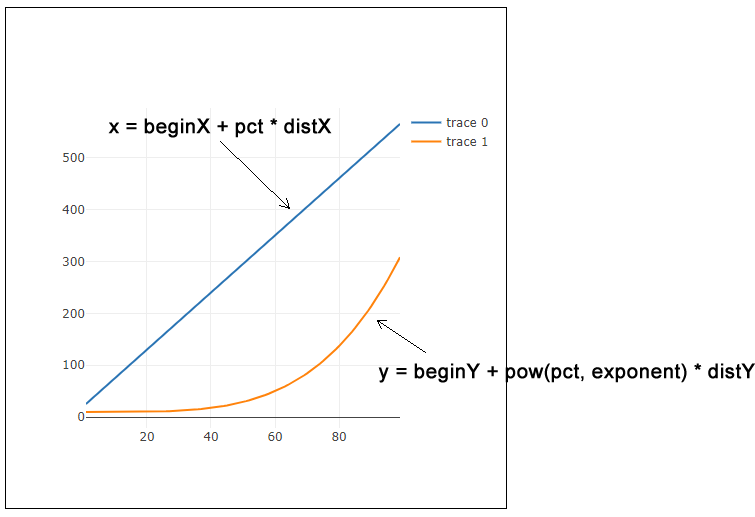
xが直線で、yが初めは穏やかに、時間がたつほど激しく変化する曲線で変化するということは、ellipse(x, y, 20, 20)で描かれる円に、X軸方向には等速、Y軸方向には加速をもたらします。yは1フレーム前のyよりも大きいので、円は下向きに曲がることになります。
xとyを入れ替えると、円は下向きに進み、その後加速して右に進みます。
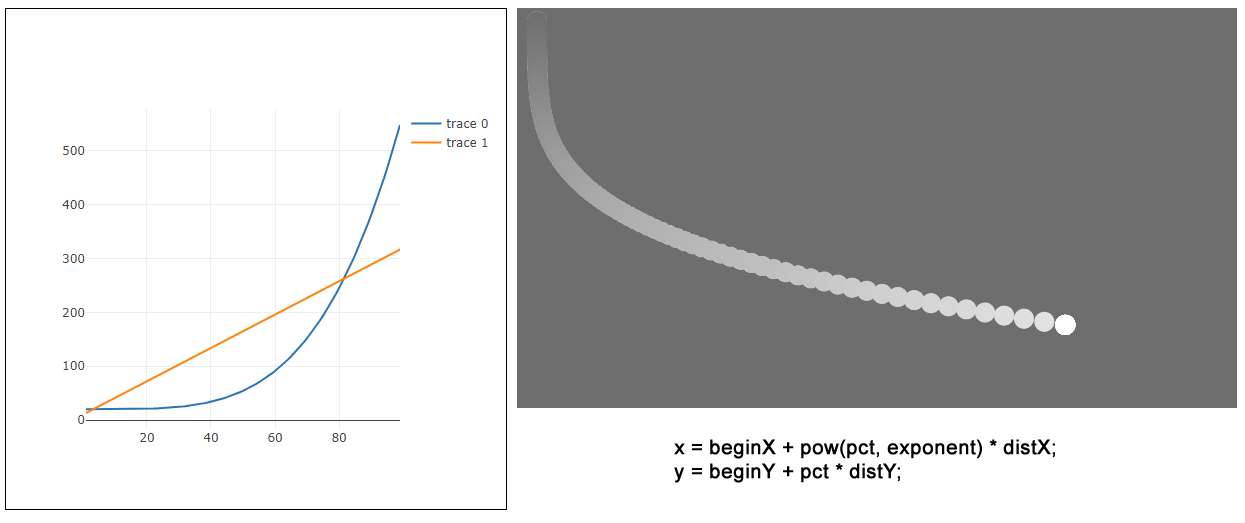
両方にy=x^4の変化を適用すると、円は直進して加速します。これはイージング関数で言う「easeInQuad」の動きです(easeInはだんだん加速する、Quadは4乗の意味)。