この記事の詳しい内容には毎日新聞の「うかび上がるのはどんな絵」ページから有料記事に進むことで読めます。
目次
概要
数字が書かれたメモがあります。数字は左から、色を塗らないマスの数と、色を塗るマスの数を表し、それらは交互に書かれています。メモの通りに色を塗ると、イラストが浮かび上がります。
下図はその例です。
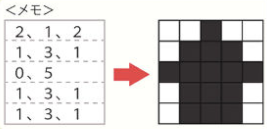
メモの1行めの「2,1,2」は、左から2マスは色を塗らず、次の1マスを塗り、以降の2マスは塗らないことを示しています。塗らないことを白、塗ることを黒に置き換えると、この行は「白、白、黒、白、白」ということになります。
2行めの「1,3,1」も同様で、左から1マスは色を塗らず、つづく3マスを塗って、最後の1マスは塗らないので、白と黒に置き換えると、「白、黒、黒、黒、白」になります。
3行めは変則的ですが、「0,5」は、左から0マスは塗らず、以降の5マスを塗るということなので、全部が黒、「黒、黒、黒、黒、黒」になります。
4行めと5行めは2行めと同じです。
ここで問題です。次のメモからはどんなイラストが浮かび上がるでしょう?

手作業で見ていく
プログラミングに取り掛かる前に、紙とペンと頭を使って考えてみましょう。
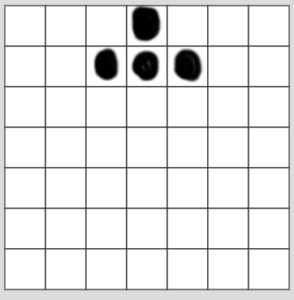
メモの縦の行数はマスの集まり(格子模様、グリッド)の行数なので、数えると7だと分かります。また各行の数字は塗るマスと塗らないマスの数です。行ごとに数字を足すと全部が7であることが分かります。つまりイラストを浮かび上がらせるグリッドは7 x 7(7行7列)です。
メモの1行めは「3,1,3」なので、これは前の例と同じように白と黒で表さすと、「白、白、白、黒、白、白、白」となります。同様に2行めは「2,3,2」なので、「白、白、黒、黒、黒、白、白」です。7 x 7のグリッドに手書きで色を入れると下図のようになります。
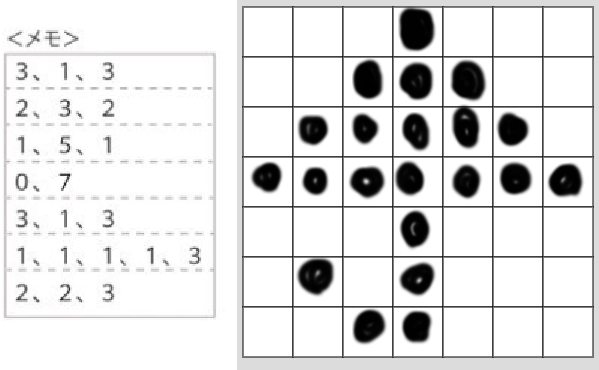
以降の行についても同様の作業をつづけると、最後、下図の右に示す傘のような形が見えてきます。これが上記お題の答えです。
論理を考える
答えは分かりましたが、これを紙とペンと頭ではなく、プログラミングで行うにはどうすればよいのでしょう? 上記手作業では、メモの1行の数字を白と黒に置き換えました。たとえば「2,1,2」は「白、白、黒、白、白」でした。以降ではこれをプログラミングの論理を考える上での取っ掛かりとしていきます。
格子模様の描画
メモの数字の行を白と黒に置き換えるこのお題の論理とは別に、マス目を並べた格子模様を描く方法を知っておく必要があります。これについては「格子ブロックのひな型コード」で述べています。
以下は5 x 5のグリッドを、幅w、高さhの矩形を並べて描くことで作成するコードです。
const rows = 5; // 横向きの行数
const columns = 5; // 縦向きの列数
const gutter = 0; // 矩形間の空き
const w = 50; // 矩形の幅
const h = 50; // 矩形の高さ
// 矩形の開始位置をずらす量 => (offsetX,offsetY)から始まる
const offsetX = 20;
const offsetY = 20;
function setup() {
createCanvas(500, 500);
background(220);
for (let c = 0; c < columns; c++) {
for (let r = 0; r < rows; r++) {
rect(offsetX + c * (gutter + w), offsetY + r * (gutter + h), w, h);
}
}
}お題では、格子模様があって、その個々のマス目を塗るか塗らないかということに着目していますが、上記コードでグリッドを描くときには、rect()関数で矩形を描く際その塗り色を黒にするか白にするかということになります。
メモの1行から始める
まずは一番簡単そうなところから始めます。例のメモの1行め、「2,1,2」を「白、白、黒、白、白」にどうやったら置き換えられるかです。
メモの数字は左から、白のマスの個数と黒のマスの個数が交互に並んでいます。「2,1,2」をプログラミングで扱いやすいように数値の配列[2,1,2]に置き換えると、この配列のインデックス番号0の要素は左から並ぶ白いマスの個数を示し、インデックス番号1の要素は黒いマスの個数を、インデックス番号2の要素は白いマスの個数を示しています。
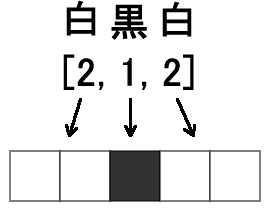
配列[2,1,2]から配列[白,白,黒,白,白]を作成する関数の作業を想像してみましょう。関数には白と黒を追加する自分用の空の配列を持たせます。配列[2,1,2]が与えられると、関数は
- 最初の要素を調べる。これは白の個数。それは2なので、空の配列に白を2つ追加する。関数の配列は[白,白]になる
- 次の要素を調べる。これは黒の個数。それは1なので、配列に黒を1つ追加する。関数の配列は[白,白,黒]になる
- 次の要素を調べる。これは白の個数。それは2なので、配列に白を2つ追加する。関数の配列は[白,白,黒,白,白]になる
関数がこのように動作すると、[2,1,2]から[白,白,黒,白,白]が作り出せそうに思えます。
しかしそうは甘くありません。数値の配列の要素数がどれも3ならよいのですが、残念ながら2つのものがあります([0,7])。また問題の方には5個のものも含まれています([1,1,1,1,3])。
要素数が3の配列を処理する関数Aと、要素が2の配列を処理する関数B、要素数が5の配列を処理する関数Cを別々に定義することもできますが、どれも似たようなコードなり、プログラムが冗長になることが想像できます。関数はさまざまな場合に対応できる柔軟性を持つものが優秀とされます。
そこで着目するのは、インデックス番号が偶数か奇数かで処理を分ける方法です。白いマスの個数と黒いマスの個数は交互に並んでいるので、インデックス番号が0,2,4…の場合には白、1,3,5…の場合には黒だと決めることができます。
値が偶数か奇数かは%演算子と2で計算した結果が0であるかどうかで分かります。%演算子は割った余りを返すので、値 % 2 が0なら割り切れたということから値は偶数、0でないなら奇数と判断できます。
if (i % 2 === 0) {
print('偶数');
}else {
print('奇数');
}次のchangeBWArray()関数は、白いマスと黒いマスの個数の配列を受け取り、それを個数分の50と255の配列に変換して返します。
function changeBWArray(arr) {
// 結果を返す配列
let resultArray = [];
// 個数の配列要素数だけ繰り返す
for (let i = 0; i < arr.length; i++) {
// 偶数の場合は塗らない(白=255)
if (i % 2 === 0) {
print('偶数');
// 個数分だけ繰り返す
// 2なら2回繰り返す
for (let j = 0; j < arr[i]; j++) {
// 2なら255を2個、追加する
resultArray.push(255);
}
// 偶数でない場合は奇数
// 奇数の場合は塗る(黒=50)
}
else {
print('奇数');
// 個数分だけ繰り返す
// 1なら1回繰り返す
for (let k = 0; k < arr[i]; k++) {
// 1なら50を1個、追加する
resultArray.push(50);
}
}
}
// 結果の配列を返す
return resultArray;
}この関数は、白を255、黒を50という数値で返します。文字列の’白’や’黒’でもかまわないのですが、fill()関数で塗り色を指定するとき、fill()関数が理解できる’white’や255に置き換える必要があります。それはいささか面倒なので、ここで数値に置き換えています。
黒を50にしているのは、矩形の枠線の色(0)と同じにしないようにするためです。50にすると少し淡い黒になるので、矩形の枠線が視認できます。
前の「格子ブロックのひな型コード」と合わせて、changeBWArray()関数を次のように使用すると、[2, 1, 2]から[255, 255, 50, 255, 255]が得られ、白、白、黒、白、白の矩形が横に並びます。
const rows = 5; // 横向きの行数
const columns = 5; // 縦向きの列数
const gutter = 0; // 矩形間の空き
const w = 50; // 矩形の幅
const h = 50; // 矩形の高さ
// 矩形の開始位置をずらす量 => (offsetX,offsetY)から始まる
const offsetX = 20;
const offsetY = 20;
function setup() {
createCanvas(300, 300);
background(220);
// 白い矩形と黒い矩形の個数を示す配列
let arr1 = [2, 1, 2];
// changeBWArray()関数に渡して、個数の配列を数値50と255の配列に変換する
// 50は黒、255は白を表す
const res = changeBWArray(arr1);
// 配列resの要素数とcolumnsの値は一致している
for (let c = 0; c < columns; c++) {
// 対応する矩形の塗り色をres配列から求める
const bw = res[c];
// その色を今の塗り色にする
fill(bw);
// 矩形を描く
rect(offsetX + c * (gutter + w), offsetY + 0 * (gutter + h), w, h);
}
}下図は描画結果です。

changeBWArray()関数を「格子ブロックのひな型コード」といっしょに動作させるには、changeBWArray()関数が返す配列の要素数がcolumns変数の値と一致している必要があります。
またrect()関数の第2引数で使っている0は、「格子ブロックのひな型コード」のrows変数が意味する行数、つまり0から始まる行番号を指しています。ここで描こうとしている[2, 1, 2]は最初の行なので、0を指定しています。
rect(offsetX + c * (gutter + w), offsetY + 0 * (gutter + h), w, h);これは、たとえば1を指定すると、0を指定した行より1行分下に描かれるということです。次はこの引数を利用して指定された行に白と黒の矩形を描画する関数を見ていきましょう。
指定された行に矩形の並びを描画する関数
changeBWArray()関数は50と255の数値の配列を返します。作成する関数にはこの配列と、描画したい行の番号(0,1,2,3…)を渡すことにします。関数名をdrawBWRectとすると、次のコードによって、
// 0行め
let arr = [2, 1, 2];
let res = changeBWArray(arr);
drawBWRect(res, 0);
// 1行め
arr = [1, 3, 1];
res = changeBWArray(arr);
drawBWRect(res, 1);下図の結果が得られるようになるということです。
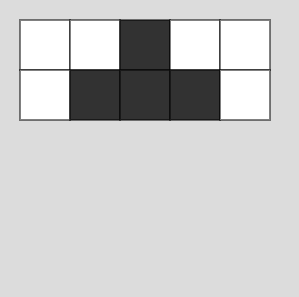
drawBWRect()関数の定義は難しくなく、前のsetup()に書いたforループを移してくるだけです。パラメータには配列arrと行番号rを用意し、rはrect()関数の第2引数に使用します。
// 0と255の配列と描画する矩形の行数(r)を受け取り、矩形を描く
// 前のsetup()内のコードを関数化したもの
function drawBWRect(arr, r) {
for (let c = 0; c < columns; c++) {
const bw = arr[c];
fill(bw);
// rはパラメータ変数
rect(offsetX + c * (gutter + w), offsetY + r * (gutter + h), w, h);
}
}すると、前の0行めと1行めのコードにつづけて、次のコードを実行すると、例の結果が得られます。
arr = [0, 5];
res = changeBWArray(arr);
drawBWRect(res, 2);
arr = [1, 3, 1];
res = changeBWArray(arr);
drawBWRect(res, 3);
arr = [1, 3, 1];
res = changeBWArray(arr);
drawBWRect(res, 4);お題を解決するプログラム
ここまでのプログラムはよくできているので、「格子ブロックのひな型コード」のcolumns変数の値とchangeBWArray()関数が返す配列の要素の数を一致させることに注意するだけで、お題の傘のイラストを描くことができます。
実際には、rows変数とcolumns変数の値を7にし、changeBWArray()関数に適切な配列を渡し、drawBWRect()に渡す行番号の数値を間違えないようにするだけです。
// お題のグリッドは7 x 7
const rows = 7;
const columns = 7;
const gutter = 0;
const w = 50;
const h = 50;
const offsetX = 20;
const offsetY = 20;
function setup() {
createCanvas(500, 500);
background(220);
// changeBWArray()関数に個数の配列を渡し、
let arr = [3, 1, 3];
let res = changeBWArray(arr);
// 返された50と255の配列と、描きたい矩形の行番号をdrawBWRect()関数に渡す
drawBWRect(res, 0);
// 同様のことを繰り返す
arr = [2, 3, 2];
res = changeBWArray(arr);
drawBWRect(res, 1);
arr = [1, 5, 1];
res = changeBWArray(arr);
drawBWRect(res, 2);
arr = [0, 7];
res = changeBWArray(arr);
drawBWRect(res, 3);
arr = [3, 1, 3];
res = changeBWArray(arr);
drawBWRect(res, 4);
arr = [1, 1, 1, 1, 3];
res = changeBWArray(arr);
drawBWRect(res, 5);
arr = [2, 2, 3];
res = changeBWArray(arr);
drawBWRect(res, 6);
}
function drawBWRect(arr, r) {
for (let c = 0; c < columns; c++) {
const bw = arr[c];
fill(bw);
rect(offsetX + c * (gutter + w), offsetY + r * (gutter + h), w, h);
}
}
function changeBWArray(arr) {
let resultArray = [];
for (let i = 0; i < arr.length; i++) {
if (i % 2 === 0) {
// print('偶数');
for (let j = 0; j < arr[i]; j++) {
resultArray.push(255);
}
}
else {
// print('奇数');
for (let k = 0; k < arr[i]; k++) {
resultArray.push(50);
}
}
}
return resultArray;
}
さらにブラッシュアップ
お題を解決するプログラムはでき上がりましたが、setup()内でのchangeBWArray()とdrawBWRect()の繰り返しが気になる場合には、さらに洗練させることもできます。
そのための方法としては、メモの数値の配列を含む大きな配列(二次元配列)を設けて、これをdrawBWRect()に処理させる方法が考えられます。
// メモの数字の配列を要素に持つ二次元配列
let orgArray = [
[2, 1, 2],
[1, 3, 1],
[0, 5],
[1, 3, 1],
[1, 3, 1]
];
function setup() {
createCanvas(300, 300);
background(220);
drawBWRect();
}
// 二次元配列を処理してグリッドを描く
function drawBWRect() {
for (let c = 0; c < columns; c++) {
for (let r = 0; r < rows; r++) {
const resArray = changeBWArray(orgArray[r]);
const bw = resArray[c];
fill(bw);
rect(offsetX + c * (gutter + w), offsetY + r * (gutter + h), w, h);
}
}
}二次元配列は構造が複雑なので、欲しい要素を取り出すときに混乱するかもしれませんが、二次元配列に含まれるメモの数字の配列のインデックス位置が行番号として使用できるので、グリッドが2重のforループで一気に描画できます。
