本稿は、毎日新聞の「プログラミング・はじめの一歩」とは関係のないオリジナル記事です。
目次
概要
アマゾンプライムビデオで「武士の家計簿」という映画を見ていたとき、草笛光子演じる祖母が孫につるかめ算の問題を出していたので、これをプログラミングで扱うとどうなるかに興味がわき、考えてみることにしました。
つるかめ算
つるかめ算(鶴亀算)とは、つるとカメが合わせて何匹(つるは何羽と数える)いて、足の数の合計が何本のとき、つるとカメはそれぞれ何匹(何羽)いるかを解く方法の1種です。「武士の家計簿」で祖母が出した問題は「つるとカメの合計は100匹で、足の数の合計は272本」でした。祖母の息子(堺雅人)はこれを5歳のとき解いたそうです。
つるの足は2本、カメの足は4本と決まっているので、問題はつるとカメの数だけ決めれば、いくつでも作れます。

さまざまな解法
つるとカメの数を出す方法はいくつもあります。つるかめ算の方法は、まだ方程式を学んでいない小学生向けのものですが、簡単かというと決してそうではなく、元々算数のセンスに欠けるわたしなどには、方程式を使った方法の方がよほど簡単に思えます。また高校で習った行列を使った解法もあります。
祖母が出した問題は数が大きいので、もっと小さな数、合計が8匹、足の合計が26本として考えることにします。
方程式を用いた解き方(中学生)
この問題は、つるとカメの数が不明で、何乗とかいっていないので、2元1次方程式で解けます。つるの数をx、カメの数をyとすると、
x + y = 8 —(1)
x*2 + y*4 = 26 —(2)
という連立2元1次方程式が成立します。つるの足は2本、カメの足は4本なので、足の合計本数は、2と4をそれぞれxとyに掛けて足すことで計算できます。
(1)のxを右辺に移項すると、y = 8 – x となり、これを(2)に代入すると、
x*2 + (8 – x)*4 = 26
となります。カッコを解いて計算すると、
2x + 32 – 4x = 26 => -2x = -6 => x = 3 となり、つるは3羽だと分かります。
カメの数は合計からつるの数を引けばよいので、8 – 3 = 5匹です。
答え:つるは3羽、カメは5匹
つるかめ算を用いた解き方1(小学生)
小学生向けのつるかめ算では、とりあえず全部がつるであると考えます。すると、
- つるが8羽いるので、足の合計本数は、8 x 2 = 16 本になる
- これは問題の本数26より10本少ない
ので、この差を、つるとカメを1匹ずつ交換することで埋めていくと考えます。具体的にいうと、つるを1羽減らし、カメ1匹増やして、足の合計本数を計算し26との差を調べます。
下の表はこの作業をつづけた結果を示しています。
| つるの数 | つるの足の本数 | カメの数 | カメの足の本数 | 足の本数の差 |
|---|---|---|---|---|
| 8 | 8*2=16 | 0 | 0*4=0 | 26 – 16 = 10 |
| 7 | 7*2=14 | 1 | 1*4=4 | 26 – 18 = 8 |
| 6 | 6*2=12 | 2 | 2*4=8 | 26 – 20 = 6 |
| 5 | 5*2=10 | 3 | 3*4=12 | 26 – 22 = 4 |
| 4 | 4*2=8 | 4 | 4*4=16 | 26 – 24 = 2 |
| 3 | 3*2=6 | 5 | 5*4=20 | 26 – 26 = 0 |
この表を見ると、つるとカメの足の合計本数が2ずつ増え、26本との差は2ずつ減って、つるの数が3、カメの数が5のとき、0になることが分かります。つまりつるとカメを交換する作業を5回繰り返すと、全部をつるとしたときの10本の差が埋まります。
つるかめ算の方法では、このような表を作成することで、答えを求めることができます。
答え:つるは3羽、カメは5匹
つるかめ算を用いた解き方2(小学生?)
実は上記の方法には、もっとスマートに済ませる方法があります。
つるの数を1ずつ減らし、カメの数を1ずつ増やすと、足の合計本数が2ずつ増えることに着目し、全部をつるとしたときの足の合計本数の差10(26 – 10)を2で割るのです。10 / 2 = 5 なので、これがカメの数になります。10 / 2 は、差(10)の中にカメの足の増分(2)がいくつ含まれるかという意味です。ここにはカメ5匹分の増分が含まれます。つるの数は全体からカメの5を引くと求まります。
答え:つるは3羽、カメは5匹
* しかし、この考え方はかなり難しくはないですか? 本当に小学生向けの解法なのでしょうか?
行列を用いた解き方(高校生)
行列の掛け算は、
![]()
と計算されるので、連立2元1次方程式は行列の掛け算で表すことができます。したがって前の、
x + y = 8
2x + 4y = 26 は、
![]() で表すことができます。
で表すことができます。
ここで表記を簡単にするため、
![]()
で表すと、AX = P となります。
行列を用いた解き方ではここで、逆行列が登場します。逆行列はA-1で表されます。逆行列は、元の行列に掛けると結果が単位行列(E)になるという性質を持っています。A・A-1 = E 単位行列は、掛けられた行列を変化させません。
AX = P に対して、両辺にAの逆行列を左から掛けます。すると、
A-1・A・X = A-1・P => X = A-1・P
となります。これで行列Xを求めることができます。
逆行列の計算については、行列Aを
![]()
とした場合、逆行列A-1は、
![]()
で計算できます。したがって、
![]()
と計算できます。
X = A-1・P は次のように計算できます。
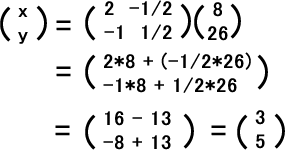
xは3、yは5だと分かります。これが答えです。
答え:つるは3羽、カメは5匹
プログラミングする
では、ここまで見てきた方法を使ってプログラミングしてみましょう。具体的に言うと、つるとカメの合計数と足の合計本数から、つるとカメのそれぞれの数を出力するプログラムを作成します。
総当たり方式のプログラム
ここまで見てきた方法を使って、と言いましたが、1つめは初出の方法です。といっても難しいものではありません。つるとカメの数に当たる2つの変数を、つるとカメの合計数まで1ずつ大きくし、それぞれの場合において、合計数と足の合計本数が問題の数に一致するかどうかを調べる、総当たりの方法です。
下図は、縦につるの数(0-8)を、横にカメの数(0-8)を取り、それに対応する足の合計本数を並べたエクセルの表です。これを見ると、足の合計本数と同じ26を表示しているセルが4つ(赤字の26)ありますが、つるとカメの合計が8になるのは、つるが3でカメが5の場合だけ(太い赤字の26)であることが分かります。
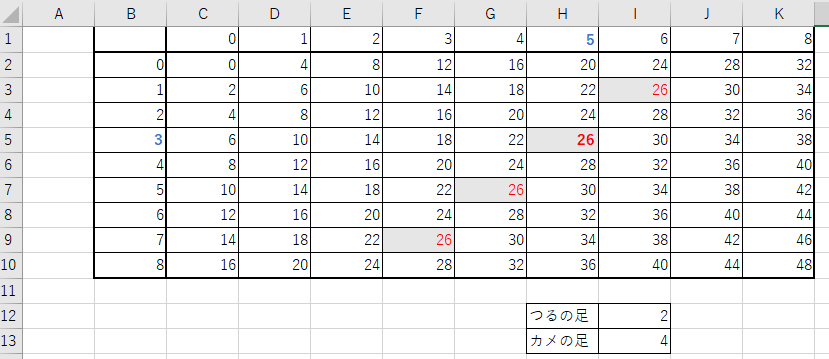
総当たりで調べるプログラムのコードには次のようなものが記述できます。
// 求めたいつるとカメの数
let craneNum;
let turtleNum;
// つるの足は2本、カメの足は4本
const craneLegs = 2;
const turtleLegs = 4;
// つるとかめの数
const totalNum = 8;
// つるとかめの足の合計数
const legTotalNum = 26;
function setup() {
noCanvas();
// 多階層forループでbreakによってループを終了させる
doubleLoop:
for (craneNum = 0; craneNum <= totalNum; craneNum++) {
print('つる: ' + craneNum);
for (turtleNum = 0; turtleNum <= totalNum; turtleNum++) {
// \tは右に字下げする
print('\tカメ: ' + turtleNum);
if (craneNum + turtleNum === totalNum) {
if (craneNum * craneLegs + turtleNum * turtleLegs === legTotalNum) {
print('つる: ' + craneNum);
print('カメ: ' + turtleNum);
// forループを抜けないと、答えが出た以降もループがつづき、無駄
break doubleLoop;
}
}
}
}
}これを実行すると、ブラウザの[コンソール]に次のように結果が出力されます。2重のforループの中に仕込んだ2つのif文が機能し、つるとカメの数の合計が26で(craneNum + turtleNum === totalNum)、かつつるの足の本数とカメの足の本数の合計が26である(craneNum * craneLegs + turtleNum * turtleLegs === legTotalNum)ときに、つるとカメの数を示す3と5が出力されています。
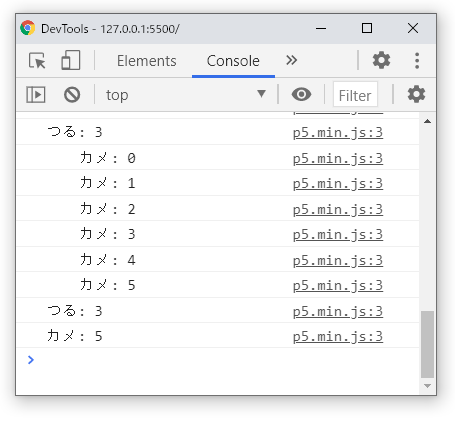
この総当たりの方法は、分からないのだから全部調べてやれという、いわば力技の方法です。スマートとはいえませんが、つるとカメの数を求めるプログラムとしては十分に通用します。人間が上記のエクセルの表を手計算で埋めるのは大変ですが、コンピュータはこの程度の計算なら一瞬でやり終えます。
なお、上記のエクセルの表ではあり得るすべての場合を計算していますが、このforループでは、2重のif文の条件が満たされたときに、breakを使って2重のforループから抜けています。つるとカメの適切な数が分かったら、もうループは必要ないので、直ちに止めるべきです。
1つめのforループの上に書いているdoubleLoop:はラベルと呼ばれるもので、このラベルをbreakの後につづけることで、2重のforループから抜けることができます。
方程式を使ったプログラム
プログラムのコードは「方程式を用いた解き方(中学生)」でも記述できます。ただしコードを書く前に準備がいります。
/*
つるの数をx、 カメの数をyとする
totalHeads = x + y-- - (1)
totalLegs = 2 x + 4 y-- - (2)
(2) の両辺を2で割る
totalLegs / 2 = x + 2 y-- - (3)
(3) のxを左辺に移項
x = totalLegs / 2 - 2 y-- - (4)
(4) を(1) に代入
totalHeads = totalLegs / 2 - 2 y + y
yをまとめる
totalHeads = totalLegs / 2 - y
*/ここまで準備できると、カメのyは「totalLegs / 2 – totalHeads」で計算できることが分かります。つるのxは「totalHeads – y」で求まります。
プログラムのコードはいたって短く記述できます。
const totalHeads = 8;
const totalLegs = 26;
let y = totalLegs / 2 - totalHeads;
print('カメ: ' + y);
print('つる :' + (totalHeads - y));しかし、このコードからは、つるとカメの足の合計本数を2で割り、そこからつるとカメの合計数を引いたものが何でカメの数になるのか、さっぱり分かりません。上記の準備をした直後なら、方程式を解いたらこうなったと覚えているでしょうが、時間がたってからコードだけを見たら、まず(少なくともわたしには)理解できないでしょう。
何よりもまず面白くありません。面白いコードとは? と聞かれても困りますが、ここからこのプログラムを発展させるダイナミズムのようなもの、アイデアをもたらす元のようなものが欠けているように、わたしには思えます。
つるかめ算を用いた解き方1(小学生)のプログラム
これは、「つるかめ算を用いた解き方1(小学生)」で述べた解法で作成するプログラムです。
とりあえず全部がつるであると考え、与えられた足の合計本数からつるの足の合計本数を引き、差を計算します。そしてその差を、つるとカメを1匹ずつ交換することで埋めていく、という考え方です。理解には前述した表が役立ちます。
コードは次のように記述できます。
let craneNum = 0;
let turtleNum = 0;
// つるの足は2本、カメの足は4本
const craneLegs = 2;
const turtleLegs = 4;
// つるとかめの数
const totalNum = 8;
// つるとかめの足の合計数
const legTotalNum = 26;
function setup() {
noCanvas();
// 全部をつるとする
craneNum = totalNum;
// 全部つるとしたときの足の数
let legs = craneNum * craneLegs;
print(legs); // 8 x 2 = 16本
print(legTotalNum - legs + '本少ない'); // 10本少ない
// 全部をつるとしたときの足の数が問題の足の数より少ないので、
if (legs < legTotalNum) {
// 足の総数が問題の足の数より少ない間、
// つるの数を1減らし、カメの数を1増やして、足の総数を計算し直す
while (legs < legTotalNum) {
craneNum--;
turtleNum++;
legs = craneNum * craneLegs + turtleNum * turtleLegs;
print(legs);
print(legTotalNum - legs + '本少ない');
}
}
// 結果を出力
print('つる' + craneNum);
print('カメ' + turtleNum);
}このプログラムでは、「つるかめ算を用いた解き方1(小学生)」の考え方に沿って、つるを1羽引いたらカメを1匹足し、その都度足の合計本数を与えられた足の合計本数と比較しているので、前述した表の数値と同じ数値が出力されます。
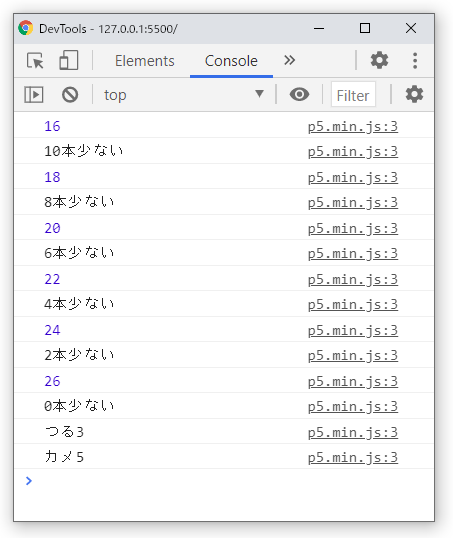
後から見ても理解できるという意味では、このプログラムが最もよくできているのではないか、とわたしは思います。
行列を用いた解き方(高校生)のプログラム
これは「行列を用いた解き方(高校生)」で見た行列を使おうとするだけのものです。コードを見ても理解できないので、実用性はありません。
次のコードでは、JavaScriptで機械学習を可能にするtensorflow.jsライブラリを使って、行列計算をしています。
// 行列Aの逆行列
const A1 = tf.tensor2d([2, -1 / 2, -1, 1 / 2], [2, 2]);
// 行列P
const P = tf.tensor2d([8, 26], [2, 1]);
// X はAの逆行列・P
let X = A1.matMul(P);
X.print();正しい答えを得ることはできます。
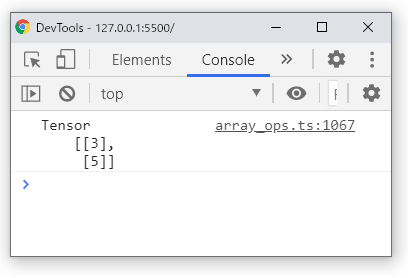
実験:機械学習は電気つるカメの夢を見るか?
以降は、適切なデータを与えて学習を積んだ機械が、つるとカメの合計数と、その足の合計本数を与えられて、正しい数を言い当てることができるのかを試す実験です。
JavaScriptとブラウザを使った機械学習を可能にするtensorflow.jsというライブラリがあるので、これを使用します。
機械学習のさわり
機械学習(マシンラーニング)とは、ごく簡単にいうと、AI(人工知能)の基本を成すものです。
スマホのアプリにも、動物や植物の写真を渡すとその種類を答えるものがありますが、これもAIの一種です。アプリは、このピクセルの並びは「ひまわり」の特徴だということを学習して知っていて、与えられた画像のピクセルの並びがそれに似ていると、「ひまわり」だと答えるわけです。
また、今の自動車には自動でブレーキをかける機能を持つものもあります。自動車のコンピュータは、人の特徴を持つピクセルの並びを学習で知っていて、カメラからの動画を頻繁に分析し、このピクセルの並びは人のピクセルの並びの特徴に近い! と判断すると、ブレーキを作動させるわけです。
ここで試そうとしているのはAIの前段階で、問題のデータ(カメの合計数とつるとカメの足の合計本数、たとえば[8,26])と、その答えのデータ(つるとカメの数、たとえば[3,5])をたくさん与えて学習させます。コンピュータはそれらのデータから関係性を導き出そうと試みます。学習はうまく進むときもあればうまくいかないときもあります。そしてこの学習訓練が終わると、コンピュータが知らない問題のデータ(たとえば[100,272])を与えます。コンピュータは、訓練の成果として得た関係性を使って、自分なりの推測を出力します。
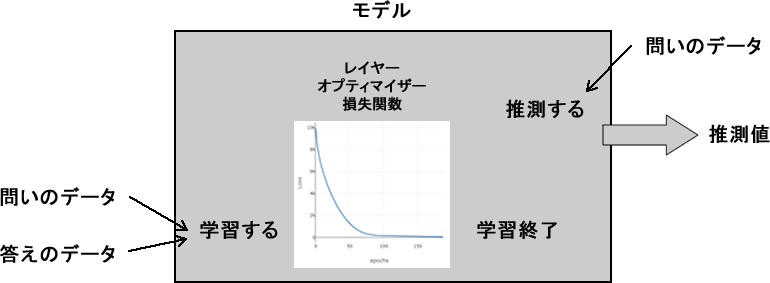
無論、コンピュータは機械なので、人間のように「考える」わけではなく、全部が計算です。tensorflow.jsでモデルと呼ばれるオブジェクトは、レイヤーやオプティマイザー、損失関数といった計算装置を持っていて、行列や微分などを使って0.00000123といった細かな数値の計算を高速に行います。
そして、ここが難問なのですが、モデルの性能は、どんなレイヤー構造にし、どのオプティマイザーと損失関数を採用するかによって出来不出来があります。どれを採用するかは、プログラマーの知識や経験がものをいうという、実に人間味のある、逆説的な問題です。
レイヤーやオプティマイザー、損失関数のうまい組み合わせでうまく学習が進むと、損失関数の出す損失値が小さくなるので、それがうまい組み合わせでうまく学習が進んでいることが分かり、まあまあのモデルだと判断できます。つまりは、やってみないと分からないということです。
機械学習を使ったプログラム
では、以下にtensorflow.jsの機械学習機能を使ったプログラムコードを記載します。tensorflow.jsを利用するにはこのライブラリをダウンロードして使えるようにする必要があります。またグラフの描画にPlotly.jsを使用するので、これもダウンロードします。そして、グラフ描画領域に使用するCSSとdiv要素も作成する必要があります。
以下はこれらを記述したHTMLファイルのコードです。
<!doctype html>
<html lang="ja">
<head>
<meta charset="UTF-8">
<title>p5.js Examples</title>
<script src="https://cdn.jsdelivr.net/npm/@tensorflow/tfjs@1.0.0/dist/tf.min.js"></script>
<script src="https://cdnjs.cloudflare.com/ajax/libs/p5.js/1.1.9/p5.min.js"></script>
<script src="https://cdn.plot.ly/plotly-latest.min.js"></script>
<style>
.graph-area {
margin: 10px;
width: 500px;
height: 500px;
border: 1px solid black;
}
.container {
display: flex;
}
</style>
</head>
<body>
<h3>機械学習によるつるカメ算</h3>
<div class="container">
<div id="chart" class="graph-area"></div>
</div>
<script src="sketch.js"></script>
</body>
</html>質問と答えに使用する数値はエクセルなどで計算できます。下図のC列つるとカメの合計とD列足の合計本数にある数値のペアが問題となるデータで、その左にあるA列つるとB列カメの数値のペアが答えのデータになります。エクセルのセルに数式を仕込んでおくと、データは、つるとカメの好きな数を入力するだけで、簡単にいくつでも作成できます。
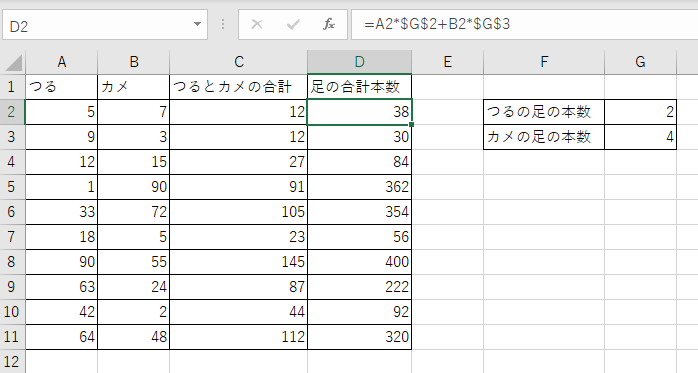
以下はわたしが記述したプログラムのコードです。
async function setup() {
noCanvas();
print('データ取得開始');
// getData()が値を返すまで次に進まない
// 訓練用データと教師用データ
const [xs, ys] = await getData();
print('データ取得完了');
print('モデル構築開始');
// buildModel()が値を返すまで次に進まない
const model = await buildModel();
print('モデル構築完了');
print('モデル訓練開始');
// モデルは与えられたxsとysから、その関係性を探る。
// 今の場合、xsはつるとカメの合計匹(羽)数と足の合計本数
// ysはそのxsに対応するつるとカメの匹(羽)数
await model.fit(xs, ys, {
epochs: 500,
// 1回の訓練が終わるたびに呼び出されるコールバック関数
// この関数を利用してグラフを描く
callbacks: {
onEpochEnd: async(epoch, logs) => {
// 繰り返しの回数を横軸に、損失値を縦軸にグラフを描く
addGraphData(epoch, logs.loss)
// 画面がフリーズしないように次のフレームに進む
await tf.nextFrame();
}
}
// 訓練が終わったら、推測
}).then(() => {
print('モデル訓練完了');
tf.tidy(() => {
// モデルに新しい値(合計匹数と合計本数)を与えて、推測させる
const res = model.predict(tf.tensor2d([100, 272], [1, 2]));
// 結果を出力
print(res.dataSync());
});
// tf.Tensorオブジェクトを破棄する
xs.dispose();
ys.dispose();
});
}
// モデルを非同期で作成する
async function buildModel() {
// レイヤーが線形に重なる基本的なモデル
const model = tf.sequential();
// 基本的な全結合レイヤーを追加
model.add(tf.layers.dense({
units: 2,
inputShape: [2]
}));
const learningRate = 0.01; // 学習率
// オプティマイザーをrmspropにする
const optimizer = tf.train.rmsprop(learningRate);
// モデルを構成
model.compile({
optimizer, // オプティマイザー
loss: 'meanSquaredError', // 損失関数
metrics: ['accuracy'],
});
return model;
}
// データを取得する
async function getData() {
// 訓練用データ(質問) => 合計匹(羽)数と足の合計本数の配列
const trainData = tf.tensor2d([
[12, 38],
[12, 30],
[27, 84],
[91, 362],
[105, 354],
[23, 56],
[145, 400],
[87, 222],
[44, 92],
[112, 320]
], [10, 2]);
// 教師用データ(答え) => つるとカメの匹(羽)数の配列
const labelData = tf.tensor2d([
[5, 7],
[9, 3],
[12, 15],
[1, 90],
[33, 72],
[18, 5],
[90, 55],
[63, 24],
[42, 2],
[64, 48]
], [10, 2]);
return [trainData, labelData];
}
// 訓練の回数と損失値の変化をグラフで描く
let xData1 = [];
let yData1 = [];
const trace = {
x: xData1,
y: yData1,
type: 'scatter'
};
const data = [trace];
const layout = {
xaxis: {
title: 'epochs'
},
yaxis: {
title: 'Loss'
},
title: '損失値の減少は学習が進んでいることを示す'
};
const addGraphData = (a, b) => {
xData1.push(a);
yData1.push(b);
Plotly.newPlot('chart', data, layout, {
displayModeBar: false
});
}これを実行すると、下図に示すような、下に向かう曲線が描かれ、やがて止まり、モデルの推測値[コンソール]に出力されます。下図ではたまたま64と36が出力されていますが、そうでないときもあります。
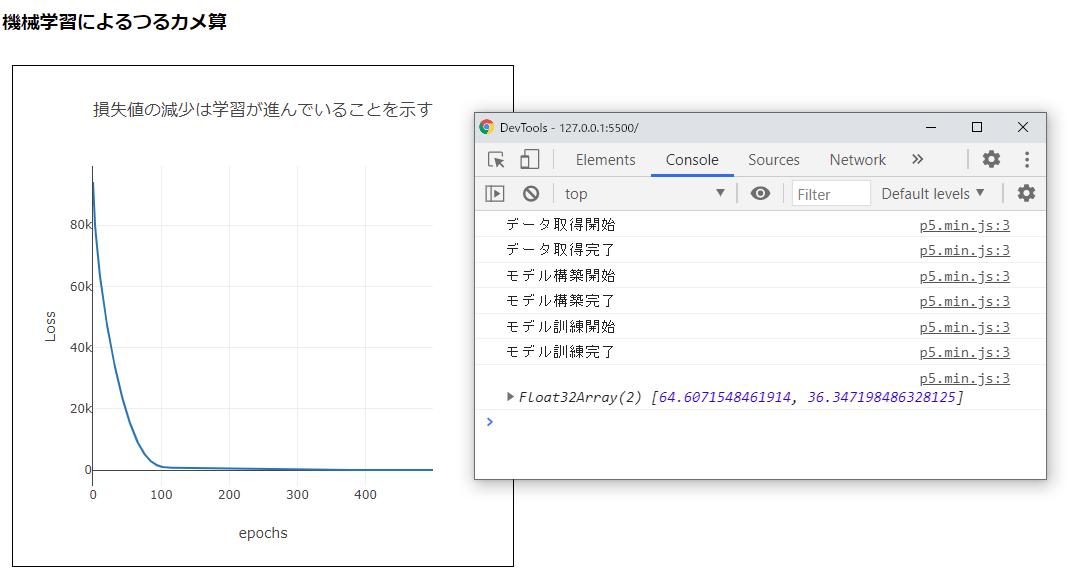
モデルに与える質問のデータ(モデルに推測させたい、未知のデータ)は、35行め当たりの tf.tidy(() => { の下、model.predict()に渡すtf.tensor2d()の第1引数の配列で指定します。このプログラムでは、合計数として100、足の合計本数として272を指定しています(祖母が孫に出した問題)。
// モデルに新しい値(合計匹数と合計本数)を与えて、推測させる
const res = model.predict(tf.tensor2d([100, 272], [1, 2]));このプログラムで驚くのは、つるの足の本数2とカメの足の本数4をどこにも指定していない点です。モデルは、ただ[12, 38] =< [5, 7]、[12, 30] => [9, 3]といった、与えられた質問と答えのデータから関係性を探り、未知の問題[100, 272]からは[64.xxx、36.xxx]が推測されると答えているのです。
