プログラミング はじめの一歩 JavaScript + p5.js編
40：番外編 何々の方へ atan2()

本稿は、毎日新聞の「プログラミング・はじめの一歩」とは関係のないオリジナル記事です。

サイン、コサインともう１つ、アークタンジェント

数学で三角関数と呼ばれるものは多くありますが、プログラミングで覚えておけばよいのは、sin()とcos()、atan2()の３つだけです。前の「番外編 円とサイン」と「番外編 サイン、コサインで三角形を描く」ではサインとコサインを取り上げています。本稿では３つめのアークタンジェントを見ていきます。

atan2()関数

アークタンジェントの数値を返すatan2()について、p5.jsのリファレンスには次のように書かれています(拙訳)。

atan2()
指定された点から座標原点への角度(ラジアン単位)を、正のX軸からの計測として計算する。値は、angleModeがRADIANSの場合にはPIから-PIの範囲の浮動小数点数として、angleModeがDEGREESの場合には180から-180の範囲の浮動小数点数として返される。atan2()関数は、ジオメトリ(形状)をカーソル位置に向けたいときによく使用される。

ノート：点のy座標が最初のパラメータで、x座標が２つめのパラメータであることに注意。これは、タンジェントの計算構造によるもの。

下図はatan2()を使っている画面を示しています。カメはイメージで、カメの頭は最初x軸の正方向(真右)を向いています。この状態でマウスカーソルを近づけると、カメの頭がカーソルの方を向きます。

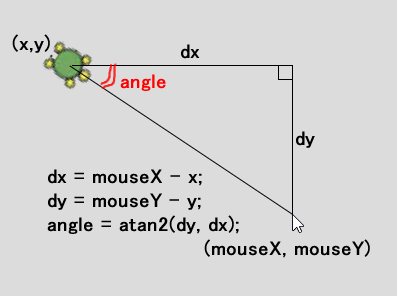
このとき知りたいのは赤字で示した角度です。これを計算するには、カーソルの位置とカメの位置との差をxとy両方向で求め、それをy、xの順番でatan2()に渡します。これだけです。

const dx = mouseX - x;		// 斜辺でない辺の長さ
const dy = mouseY - y;		// 斜辺でない辺の長さ
const angle = atan2(dy, dx);	// x軸との角度

atan2()関数は、直角三角形の、斜辺でない２辺の長さが分かっていて、x軸との角度を知りたいときに使用できます。三角関数では基本的に角度をラジアン単位(PIが180度)で扱いますが、これが分かりづらいという場合には、p5.jsのangleMode(DEGREES)をsetup()関数内で呼び出しておきます。すると角度が度単位で扱えるようになります。

点p!から点p2まで線が伸びるアニメーション

以降では、下図に示すように、点p1から点p2まで線が伸びていくアニメーションの作成方法を考えていきます。ここまで述べてきたatan2()関数が使用できますが、使わなくても解決できます。

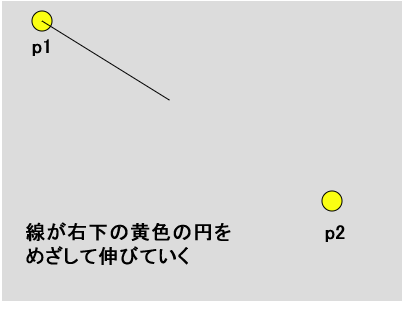
atan2()を使わない方法

まずはatan2()関数を知らなくても実現できる方法からです。

点p1と点p2の位置は分かっているので、x方向の差はp2のx座標からp1のx座標を引き、y方向の差はp2のy座標からp1のy座標を引くことで簡単に分かります。

const dx = p2.x - p1.x;
const dy = p2.y - p1.y;

このdxとdyは、p1とp2の座標の差ですが、距離でもあります。もし次のフレームでp1からx方向にdxだけ、y方向にdyだけ移動すると、p2の位置に移動します。

ということは、アニメーションにかけたい時間に相当するフレーム数でdxとdyを割ると、それは、1フレーム当たりのxとy方向の移動量になる、ということです。

const frames = 240;		// アニメーションにかけるフレーム数
const moveX = dx / frames;	// 1フレーム当たりのx方向の移動量
const moveY = dy / frames;	// 1フレーム当たりのy方向の移動量

すると、この移動量を毎フレーム、線の終端に足すと、線はp2に向かって伸びていくということになります。

line(p1.x, p1.y, endX, endY);
endX += moveX;
endY += moveY;

下図はこの考え方を説明しています。これは、まず全体を見通し、1フレームで移動すべき量を割り出して、それを実際に足していくという方法です。

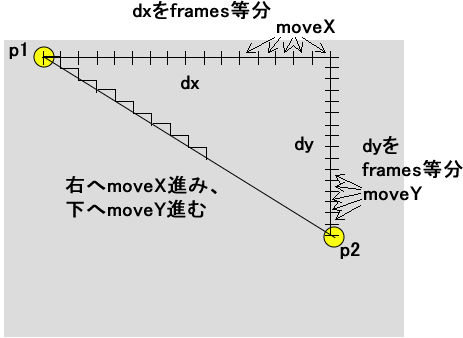
ここまでをコードにまとめると、次のように記述できます。

let p1, p2; // 開始と終了位置を表すオブジェクト
const frames = 240; // アニメーションにかけるフレーム数(=４秒)
let count = 0; // 線の描画開始からのフレーム数を数える
let endX, endY; // 線の終端
let moveX, moveY; // 1フレーム当たりの移動量
let isAction = false;

function setup() {
    createCanvas(400, 300);
    p1 = {
        x: 40,
        y: 20
    }; // 開始位置は(40,20)
    p2 = {
        x: 330,
        y: 200
    }; // 終了位置は(330,200)
    endX = p1.x; // 線の終端は、最初線の開始位置
    endY = p1.y;
    const dx = p2.x - p1.x; // 開始位置と終了位置の差(=辺の長さ)
    const dy = p2.y - p1.y;
    moveX = dx / frames; // 差をフレーム数で割ると、
    moveY = dy / frames; // 1フレーム当たりの、移動すればよい量が計算できる
}

function draw() {
    background(220);
    // 開始点と終了点を黄色の円で示す
    fill(255, 255, 0);
    ellipse(p1.x, p1.y, 20, 20);
    ellipse(p2.x, p2.y, 20, 20);
    // マウスプレスで開始
    if (isAction) {
        // 線を描画 => endXとendYの値が毎フレームmoveXとmoveYだけ大きくなるので、
        // 線はp2に向かって長くなる
        line(p1.x, p1.y, endX, endY);
        if (count <= frames) {
            endX += moveX;
            endY += moveY;
        }
        count++;
    }
}

function mousePressed() {
    isAction = !isAction;
}

下は実行画面です。画面のクリックで線が伸びるアニメーションが始まります。

atan2()を使った方法

前のatan2()を使わない方法が全体を見通す方法であったのに対し、atan2()を使った方法は、向かうべき方向を確定し、すぐ1フレーム先の移動先への移動を繰り返すという方法です。

p1とp2の位置は分かっているので、直角三角形の斜辺でない辺の長さdxとdyは簡単に計算できます。この２つの値とatan2()から、向かうべき方向はx軸からの角度として分かります。すると次のフレームでいるべき位置は、今いる位置を(0,0)とした場合の円の円周上の点の計算で求めることができます。

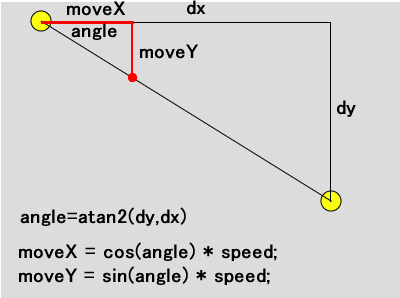
この考え方をコードで表すと次のように記述できます。結果は前と同じですが、変数speedの値を変えると線を描くスピードが変わります。

let p1, p2; // 開始と終了位置を表すオブジェクト
let endX, endY; // 線の終端
let moveX, moveY; // 1フレーム当たりの移動量
let isAction = false;

// 円の半径に当たる値
const speed = 2;

function setup() {
    createCanvas(400, 300);
    p1 = {
        x: 40,
        y: 20
    }; // 開始位置は(40,20)
    p2 = {
        x: 330,
        y: 200
    }; // 終了位置は(330,200)
    endX = p1.x; // 最初の線の終わりはp1
    endY = p1.y;

    const dx = p2.x - p1.x; // 開始位置と終了位置の差(辺の長さ)
    const dy = p2.y - p1.y;
    // 開始点と終了点で形成される直角三角形の角度を求める
    // => 開始点からこの角度の方向に進めば終了点があることになる
    const angle = atan2(dy, dx);
    // 開始点を(0,0)としたときの、半径speed上にある円周上の点(moveX, moveY)
    // => 1フレーム当たりの移動量と見なすことができる
    moveX = cos(angle) * speed;
    moveY = sin(angle) * speed;
}

// draw()関数は前と同じ
function draw() {
    background(220);
    // 開始点と終了点を黄色の円で示す
    fill(255, 255, 0);
    ellipse(p1.x, p1.y, 20, 20);
    ellipse(p2.x, p2.y, 20, 20);
    // マウスプレスで開始
    if (isAction) {
        // 線を描画 => endXとendYの値が毎フレームmoveXとmoveYだけ大きくなるので、
        // 線はp2に向かって長くなる
        line(p1.x, p1.y, endX, endY);
        if (endX < p2.x) {
            endX += moveX;
            endY += moveY;
        }
    }
}

function mousePressed() {
    isAction = !isAction;
}

atan2()を使った方法の特徴の１つは、あらかじめ全体を見通す必要がないということです。これは、向かう先を途中でも変えられるということです。

点p!からマウスまで線が伸びるアニメーション

atan2()を使うと、点p1から出た線が、移動をつづけるマウスまで伸びるアニメーションが作成できます。線の終端がマウスカーソルを追いかけているような効果が生まれます。

プログラムの実行中でも、線の終端の行先を変えられるようにするには、辺の長さと角度、移動量を毎フレーム計算し、moveXとmoveYを求めます。関数にまとめると分かりやすいので、次のcalcMoveXY()はdraw()内に置きます。

// 1フレームでの移動量を計算する
function calcMoveXY() {
    const dx = mouseX - p2.x; // 辺の長さ
    const dy = mouseY - p2.y;
    const angle = atan2(dy, dx); // 角度
    moveX = cos(angle) * speed; // その方向へ向かう移動量
    moveY = sin(angle) * speed;
}

以下はその例です。

let p1, p2; // 開始と終了位置を表すオブジェクト
let moveX, moveY; // 1フレーム当たりの移動量
let isAction = false;

// 円の半径に当たる値、振幅
const speed = 2;

function setup() {
    createCanvas(400, 300);
    angleMode(DEGREES);
    p1 = {
        x: 40,
        y: 20
    }; // 開始位置は(40,20)
    p2 = {
        x: 40,
        y: 20
    }; // 終了位置は(330,200)
}

function draw() {
    background(220);
    fill(255, 255, 0);
    ellipse(p1.x, p1.y, 20, 20);
    fill(255, 0, 0);
    // p2は変化するので、赤い円は移動する
    ellipse(p2.x, p2.y, 20, 20);
    // 黄色の円と赤い円を線で結ぶ
    line(p1.x, p1.y, p2.x, p2.y);
    // 赤い円の1フレームでの移動量を計算する
    calcMoveXY();
    // p2はマウスに向かって移動する
    if (isAction) {
        p2.x += moveX;
        p2.y += moveY;
    }
}

// 1フレームでの移動量を計算する
function calcMoveXY() {
    const dx = mouseX - p2.x; // 辺の長さ
    const dy = mouseY - p2.y;
    const angle = atan2(dy, dx); // 角度
    moveX = cos(angle) * speed; // その方向へ向かう移動量
    moveY = sin(angle) * speed;
}

function mousePressed() {
    isAction = !isAction;
}

下は実行画面です。画面のクリックで線が伸びるアニメーションが始まり、マウスを動かすと線もそこをめざして伸びてきます。

不思議な物体を複数のカメが見つづける

画面上を円が周回し、それをカメが見つづけます。カメは最初１匹いるだけですが、画面のマウスクリックでいくつでもクリックした位置に作成できます。

let kameImage;
let kames = [];
let centerX, centerY;
let mysteriousO; // カメが見つづけるターゲットにするオブジェクト

function preload() {
    kameImage = loadImage('images/kame.png');
}

function setup() {
    createCanvas(400, 300);
    angleMode(DEGREES);
    imageMode(CENTER);
    centerX = width / 2;
    centerY = height / 2;
    // カメはこのオブジェクトを見つづける
    mysteriousO = {
        x: 0,
        y: 0,
        r: 50,
        angle: 0,
        cx: centerX,
        cy: centerY
    };
    // 最初、カメを1匹だけ画面センターに作成
    const kame = new Kame(centerX, centerY, kameImage, mysteriousO);
    kames.push(kame);
}

function draw() {
        background(220);
        mysteriousAction(); // 円の周回アニメーション
        // kameインスタンスがkames配列に含まれているなら
        if (kames.length > 0) {
            // 配列内のkameインスタンスにアクセスして
            for (let i = 0; i < kames.length; i++) {
                // kameから周回する円までの距離
                const kameX = kames[i].getX();
                const kameY = kames[i].getY();
                // kameをターゲットの方に向かせる
                kames[i].rotateAndDisplay();
            }
        }
    }
    // 画面のマウスプレスでKameインスタンスを作成し、配列に追加
function mousePressed() {
    const kame = new Kame(mouseX, mouseY, kameImage, mysteriousO)
    kames.push(kame);
}

class Kame {
    constructor(x, y, img, target) {
        this.x = x;
        this.y = y;
        this.image = img;
        this.target = target;
    }
    getX() {
        return this.x;
    }
    getY() {
        return this.y;
    }
    display() {
            // 座標システムの原点にカメを描画
            image(this.image, 0, 0);
        }
        // ターゲット方向に回転して描画
    rotateAndDisplay() {
        // atan2()で角度を計算
        const dx = this.target.x - this.x;
        const dy = this.target.y - this.y;
        const angle = atan2(dy, dx);
        // 座標変換を限定する
        push();
        // 自分自身の(x,y)に座標システムの原点を移動
        translate(this.x, this.y);
        // 座標システムの原点を中心にangle度回転
        rotate(angle);
        // 座標システムの原点に描画
        this.display();
        // translate(-this.x, -this.y);で戻した場合には
        // image(this.image, this.x, this.y)になる
        pop();
    }
}
// 円の周回運動
function mysteriousAction() {
    mysteriousO.x = mysteriousO.cx + cos(mysteriousO.angle) * mysteriousO.r * 3;
    mysteriousO.y = mysteriousO.cy + sin(mysteriousO.angle) * mysteriousO.r;
    ellipse(mysteriousO.x, mysteriousO.y, mysteriousO.r);
    mysteriousO.angle++;
}

下は実行画面です。カメは画面のクリックでいくつでも増やすことができます。