プログラミング はじめの一歩 JavaScript + p5.js編
41：番外編 アナログ時計を作成

本稿は、毎日新聞の「プログラミング・はじめの一歩」とは関係のないオリジナル記事です。

概要

「番外編 円とサイン」や「番外編 サイン、コサインで三角形を描く」で見たサイン、コサインは、アナログ時計の作成にも利用できます。具体的には、文字盤の数字(1やIなど)の配置や長針、短針の描画です。

下は、以降で作成するアナログ時計です。厳密には、デジタルで動作するアナログ時計もどきです。

時刻の取得

時計を作成するには、まず今の時刻を調べる必要があります。コンピュータには時計が内蔵されており、p5.jsの関数から調べることができます。今が何時かはhour()で、何分かはminute()で、何秒かはsecond()関数でそれぞれ分かります。どれも直感的で分かりやすい関数ですが、hour()は結果を24時間表記で返すのが特徴的です。たとえば3は午前３時で、15は午後３時を意味します。

hour()
説明
p5.jsはコンピュータの時計とやりとりする。hour()関数は現在の時を0から23の値として返す(24時間表記)。
シンタックス
hour()
戻り
整数: 現在の時数

minute()
説明
p5.jsはコンピュータの時計とやりとりする。minute()関数は現在の分を0から59の値として返す。
シンタックス
minute()
戻り
整数: 現在の分数

second()
説明
p5.jsはコンピュータの時計とやりとりする。second()関数は現在の秒を0から59の値として返す。
シンタックス
second()
戻り
整数: 現在の秒数

次のコードは簡単な使用例です。

function setup() {
    createCanvas(200, 100);
    textSize(30);
}

function draw() {
    background(220);
    const h = hour();
    text(h, 20, 50); // 24時間表記
    const m = minute();
    text(m, 70, 50);
    const s = second();
    text(s, 120, 50);
}

下図は実行例です。午後に実行したので、15時41分26秒を示しています。

文字盤の数字

現在時刻の調べ方が分かったので、次は長針や短針の作成に移りたいところですが、その前に文字盤の数字の描画方法を見ていきましょう。一般的には時を表す1から12のアラビア数字が使用されますが、IからXIIまでのローマ数字が使われる時計もあります。

サインとコサインの使用

文字盤の数字はサインとコサインで配置できます。具体的に言うと、中心が(cy,cy)、半径がradiusである円を想定します(これが時計の背景になります)。すると、「番外編 円とサイン」や「番外編 サイン、コサインで三角形を描く」で何回も使った次のコードで、数字の位置(x,y)が特定できます。

const x = cx + cos(angle) * radius;
const y = cy + sin(angle) * radius;

このとき覚えておく必要があるのは、角度が0のときの(cos(0),sin(0))は、円の中心から真右の円周上の点に来るということです。ここに来させたいのは3です。また数字は1から12の12個を配置するので、隣りの数字との角度の差は30度になります(360 / 12 = 30)。

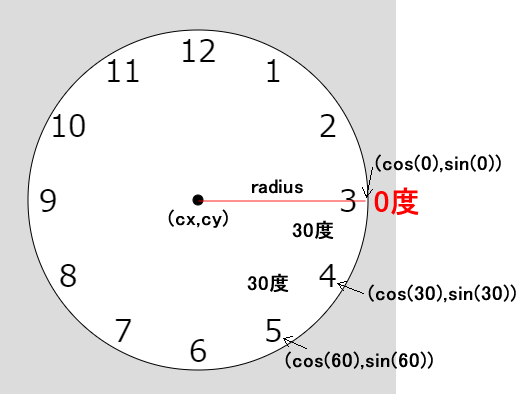
数字を位置を決めるとき、何も考えないで、次のように、0から始め(angle = 0)、30度刻みに(angle += 30)、360度未満まで(angle < 360)繰り返したとします。

let h = 0; // 時数
for (let angle = 0; angle < 360; angle += 30) {
    // 時数に1足す
    h++;
    const x = cx + cos(angle) * radius;
    const y = cy + sin(angle) * radius;
    // 時数を描画
    text(h, x, y);
}

すると、下図に示すように、本来3が来てほしい位置に1が来ます。これは、hが1のときangleが0であるからです。1は-60度の位置に来させたいので、そのためには、反時計回りに60度ずらします。

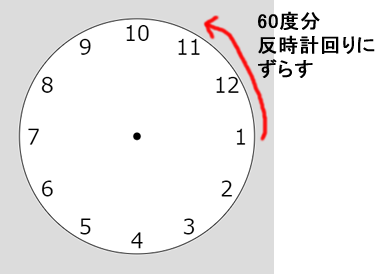
反時計回りに60度ずらすには、-60から始め、30度刻みで、270以下まで繰り返すようforループを修正します。

for (let angle = -60; angle <= 270; angle += 30) {

下図は、変数angleの値を、そのときに時数の下に赤字で示しています。

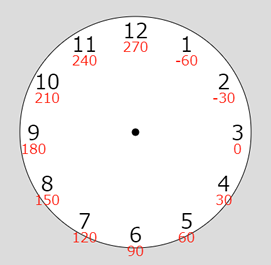
これで、文字盤の数字が描画できるようになりました。以下はここまでをまとめたコードです。

let cx, cy; // 円形時計の中心(キャンバスセンター)
let radius; // 円形時計の半径

function setup() {
    createCanvas(400, 400); // キャンバスは正方形
    angleMode(DEGREES); // 角度は度数で数える
    textSize(30);
    textAlign(CENTER);
    cx = width / 2; // キャンバスのセンター
    cy = height / 2;
    radius = cx - 30; // 時計の半径はキャンバスの幅半分より少し小さくする
}

// 毎フレーム、時計を描画しつづける
function draw() {
    background(220);
    // 重なりが下(奥)のものから描く
    drawCircle();
    drawIndex();
    drawCenter();
}

// 円形時計の白い背景
function drawCircle() {
    fill(255);
    ellipse(cx, cy, radius * 2);
}

// 文字盤
function drawIndex() {
        fill(0);
        let count = 0;
        // 数字を角度の配列とサイン、コサインを使って円状に描く
        for (let angle = -60; angle <= 270; angle += 30) {
            const x = cx + cos(angle) * (radius - 20);
            const y = cy + sin(angle) * (radius - 20) + 10;
            count++;
            text(count, x, y);
        }
    }
    // 針のセンターの黒丸
function drawCenter() {
    fill(0);
    ellipse(cx, cy, 10);
}

３つの針の描画

針の描画はアナログ時計プログラム最大の問題です。針は長針、短針、秒針の３つがあり、動きがそれぞれ異なります。こういう場合には、１度にやろうとせず、一番簡単そうに思えるものから取りかかるのがポイントです。

針自体の描画

針そのものは、line()関数が描画する線で表現できます。line()関数には、次のように、始点となる(x1,y1)と終点の(x2,y2)を与えるだけなので、簡単です。また秒針は細く、長針はそれより太く、短針はもっと太くしたいわけですが、これもstrokeWeight()関数で解決できます。

strokeWeight(1);
line(x1, y1, x2, y2)

線の始点は時計の円の中心(cx,cy)です。そして問題は、線の終点(x2,y2)をどうやって求めるか、です。次は、最も簡単そうに思える秒針を見ていきます。

秒針の描画

今この瞬間の秒数は、前に述べたsecond()関数で分かります。秒数を文字で表示するだけならsecond()が返す数値を描画するだけで済みますが、ここではこの数値を角度で表す必要があります。

次のコードは、角度を変数sAngleとしたときの秒針を描画する例です。秒針の線の太さはstrokeWeight(1)で、長さはsecHandLengthで指定します。線の終点は、(cx,cy)を中心とする半径secHandLengthの円の円周上の点になります。

let secHandLength;

function setup() {
    ...
    secHandLength = radius - 30; // 秒針は半径より少し短くする
}

function draw() {
    ...
    drawSecHand();
}

function drawSecHand() {
    let sAngle = 0;
    strokeWeight(1);
    line(cx, cy, cx + cos(sAngle) * secHandLength, cy + sin(sAngle) * secHandLength);
}

上記コードではsAngle=0なので、線は(cx,cy)から真右に３時の方向に描かれます(下図左)。同様に90度のとき線は６時の方向に描かれ(下図真ん中)、45度のときは４時と５時の間を指して描かれます(下図右)。

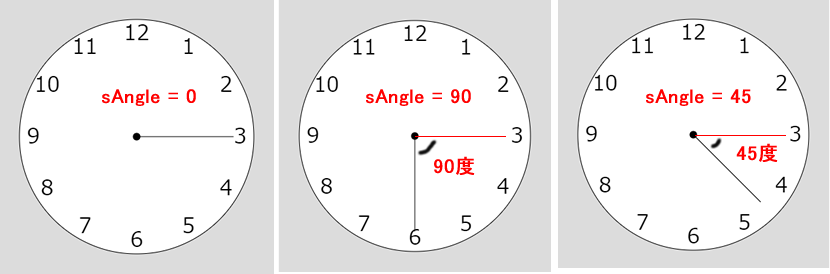
ではsAngleの数値はどうやって決めればよいのでしょう？ これは、second()が返す秒数を角度に変換するということです。頭の中が真っ白になるかもしれませんが、落ち着いて考えましょう。

秒針は60秒で文字盤を１周するので、360度回転します。これは、60秒が360度に対応しているということです。ここから、

60秒:360度 = 1秒:x度

という比の関係が成り立ちます。比では「内項の積と外項の積は等しい」ことが成り立つので、60x = 360 => x = 360/60 から、1秒で6度回転するということが分かります。

この比の計算にはp5.jsのmap()関数が利用できます(「マッピング(対応付け)」参照)。次のコードは、0秒から60秒の範囲にあるsecond()関数が返す値を、0度から360度の範囲に換算する、という意味です。

let sAngle = map(second(), 0, 60, 0, 360);

秒数の角度への変換はこれで行えますが、プログラムを実行し、「日本時間と現在時刻」などのページで実際の現在秒と比べると、下図に示すように、15秒早いことが分かります。これは、実際の秒は12時の方向から始まるのに対し、sin()とcos()は3時の方向から始まることに起因しています。

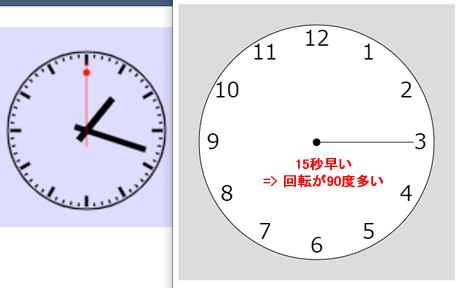
この問題の解決は簡単で、15秒に相当する角度90度を引けばよいだけです。

let sAngle = map(second(), 0, 60, 0, 360) - 90;

ここまでで秒針が描画できるようになります。以下はそのコード全文です。

let cx, cy; // 円形時計の中心(キャンバスセンター)
let radius; // 円形時計の半径

let secHandLength; // 秒針の長さ

function setup() {
    createCanvas(400, 400); // キャンバスは正方形
    angleMode(DEGREES); // 角度は度数で数える
    textSize(30);
    textAlign(CENTER);
    cx = width / 2; // キャンバスのセンター
    cy = height / 2;
    radius = cx - 30; // 時計の半径はキャンバスの幅半分より少し小さくする

    secHandLength = radius - 30; // 秒針は半径より少し短くする
}

// 毎フレーム、時計を描画しつづける
function draw() {
    background(220);
    // 重なりが下(奥)のものから描く
    drawCircle();
    drawIndex();
    drawCenter();
    // 秒針を描画
    drawSecHand()
}

// 円形時計の白い背景
function drawCircle() {
    fill(255);
    ellipse(cx, cy, radius * 2);
}

// 文字盤
function drawIndex() {
        fill(0);
        let count = 0;
        // 数字を角度の配列とサイン、コサインを使って円状に描く
        for (let angle = -60; angle <= 270; angle += 30) {
            const x = cx + cos(angle) * (radius - 20);
            const y = cy + sin(angle) * (radius - 20) + 10;
            count++;
            text(count, x, y);
        }
    }
    // 針のセンターの黒丸
function drawCenter() {
        fill(0);
        ellipse(cx, cy, 10);
    }
    // 秒針を描画する
function drawSecHand() {
    // 秒数を角度に変換
    let sAngle = map(second(), 0, 60, 0, 360) - 90;
    strokeWeight(1);
    // 線の終点は、(cx,cy)を中心とする半径secHandLengthの円の円周上の点
    line(cx, cy, cx + cos(sAngle) * secHandLength, cy + sin(sAngle) * secHandLength);
}

下は上記コードの実行画面です。

長針の描画

長針(分針)の描画は秒針の描画と基本的に変わりません。minHandLengthといった名前の変数をグローバル変数として宣言しておいて、setup()関数内で長さを決め(minHandLength = radius – 50)、長針を描画する関数を定義して、それをdraw()内で呼び出します。次のdrawMinHand()関数はその例です。

// 長針を描画する
function drawMinHand() {
    let mAngle = map(minute(), 0, 60, 0, 360) - 90;
    strokeWeight(2); // 秒針より太くする
    line(cx, cy, cx + cos(mAngle) * minHandLength, cy + sin(mAngle) * minHandLength);
}

この関数を前述したプログラムコードに組み込んで実行し、１分ほどながめます。すると、長針が動くのは、秒針が12を指したときだけということが分かります。つまりいきなり１分が経過するように見えるわけです。second()関数が返す値が変化するのは、現在の分数が変わったときなので、当然こうなります。

ではいきなり1分分(6度)動くのではなく、1分かけて滑らかに動くようにするにはどうすればよいでしょう？ 滑らかに動くということは、小さな角度が足されていくということなので、minute()だけでなく、second()が返す秒数も分数扱いで加えるということです。この”秒の分扱い”にはp5.jsのnorm()関数が利用できます。

// 0から60の範囲の数値であるsecond()が返す値を正規化(0から1の間の数値に変換)
// => その秒数が何%分かに当たる　30秒なら0.5、50%
const normalizedValue = norm(second(), 0, 60);
// 現在の分数に、分に換算した秒数を足す
const minutePlus = minute() + normalizedValue;
const mAngle = map(minutePlus, 0, 60, 0, 360) - 90;

norm()
説明
別の範囲の数値を0と1の間の値に正規化する。map(value, low, high, 0, 1)と同じ。範囲外の数値は、そのように意図されたもので有用な場合が多いことから、0と1の間に限定されない。
シンタックス
norm(value, start, stop)
パラメータ
value 数値 正規化される入力値
start 数値: 値の現在の範囲の下限
stop Number: 値の現在の範囲の上限
戻り
数値: 正規化された数値

短針の描画

短針は長針と同じ要領で作成できます。長針のコードでnorm()を使って角度を求めた３行は１行に短くできます。

// 短針を描画する
function drawHourHand() {
    // 正規化しマッピングする上記３行は次の１行に短くできる
    const hAngle = map(hour() + norm(minute(), 0, 60), 0, 24, 0, 360 * 2) - 90;
    strokeWeight(4); // 短針より太くする
    line(cx, cy, cx + cos(hAngle) * hourHandLength, cy + sin(hAngle) * hourHandLength);
}

アナログ時計プログラムコード全文

以下は、本稿最初で示したアナログ時計プログラムのコード全文です。アラビア数字の代わりにローマ数字を使っています。

let cx, cy; // 円形時計の中心(キャンバスセンター)
let radius; // 円形時計の半径

let secHandLength; // 秒針の長さ
let minHandLength; // 長針の長さ
let hourHandLength; // 短針の長さ

// 文字盤に使用するローマ文字の配列 1から12
let romans = ['I', 'II', 'III', 'IV', 'V', 'VI', 'VII', 'VIII', 'IX', 'X', 'XI', 'XII'];

function setup() {
    createCanvas(400, 400); // キャンバスは正方形
    angleMode(DEGREES); // 角度は度数で数える
    textSize(20);
    textAlign(CENTER);
    cx = width / 2; // キャンバスのセンター
    cy = height / 2;
    radius = cx - 30; // 時計の半径はキャンバスの幅半分より少し小さくする

    secHandLength = radius - 30; // 秒針は半径より少し短くする
    minHandLength = radius - 50; // 長針は半径より短くする
    hourHandLength = radius - 70; // 短針は半径よりもっと短くする
}

// 毎フレーム、時計を描画しつづける
function draw() {
    background(220);
    // 重なりが下(奥)のものから描く
    drawCircle();
    drawIndex();
    drawCenter();
    drawSecHand(); // 秒針を描画
    drawMinHand(); // 長針を描画
    drawHourHand() // 短針を描画
}

// 円形時計の白い背景
function drawCircle() {
    fill(255);
    ellipse(cx, cy, radius * 2);
}

// 文字盤
function drawIndex() {
        fill(0);
        let count = 0;
        // ローマ文字を角度の配列とサイン、コサインを使って円状に描く
        for (let angle = -60; angle <= 270; angle += 30) {
            const x = cx + cos(angle) * (radius - 20);
            const y = cy + sin(angle) * (radius - 20) + 10;
            text(romans[count], x, y);
            count++;
        }
    }
    // 針のセンターの黒丸
function drawCenter() {
        fill(0);
        ellipse(cx, cy, 10);
    }
    // 秒針を描画する
function drawSecHand() {
        // 秒数を角度に変換
        let sAngle = map(second(), 0, 60, 0, 360) - 90;
        strokeWeight(1);
        // 線の終点は、(cx,cy)を中心とする半径secHandLengthの円の円周上の点
        line(cx, cy, cx + cos(sAngle) * secHandLength, cy + sin(sAngle) * secHandLength);
    }
    // 長針を描画する
function drawMinHand() {
    // 0から60の範囲の数値であるsecond()が返す値を正規化(0から1の間の数値に変換)
    // => その秒数が何%分かに当たる　30秒なら0.5、50%
    const normalizedValue = norm(second(), 0, 60);
    // 現在の分数に、分に換算した秒数を足す
    const minutePlus = minute() + normalizedValue;
    const mAngle = map(minutePlus, 0, 60, 0, 360) - 90;
    //let mAngle = map(minute(), 0, 60, 0, 360) - 90;
    strokeWeight(2); // 秒針より太くする
    line(cx, cy, cx + cos(mAngle) * minHandLength, cy + sin(mAngle) * minHandLength);
}

// 短針を描画する
function drawHourHand() {
    // 正規化しマッピングする上記３行は次の１行に短くできる
    const hAngle = map(hour() + norm(minute(), 0, 60), 0, 24, 0, 360 * 2) - 90;
    strokeWeight(4); // 短針より太くする
    line(cx, cy, cx + cos(hAngle) * hourHandLength, cy + sin(hAngle) * hourHandLength);
}