4_2 同じ問題に対して、異なるTensorFlow.jsモデルを試す

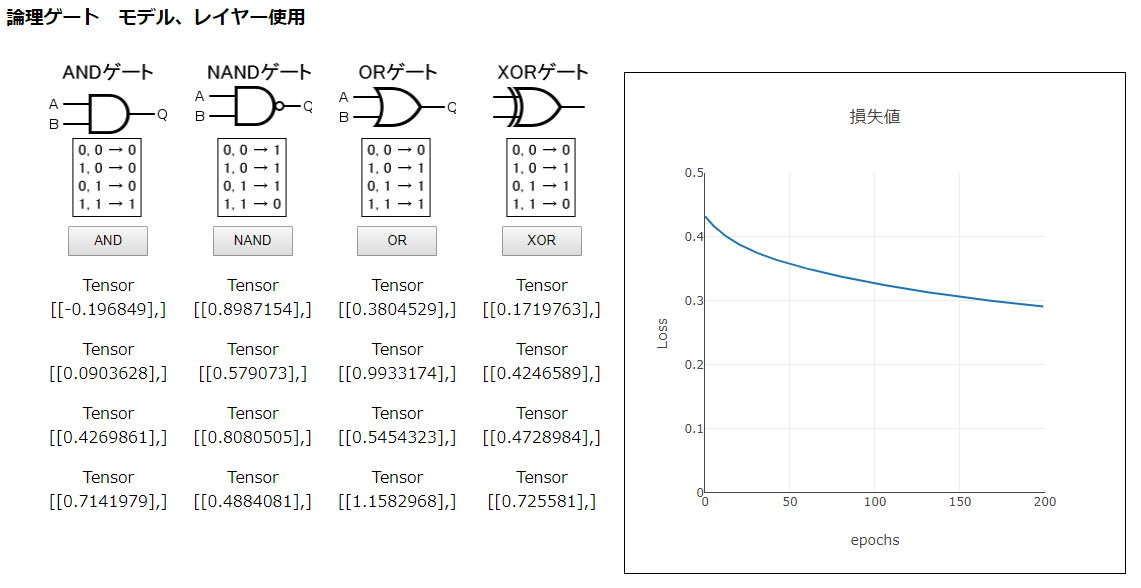
まず、前の「3_1_2 モデルの作成」で使ったモデルで試してみます。

const model = tf.sequential();
model.add(tf.layers.dense({units: 1, inputShape: [2]}));
model.compile({ loss: 'meanSquaredError', optimizer: 'sgd' });

損失値の減り具合や、推測値の結果から見て、うまくありません。

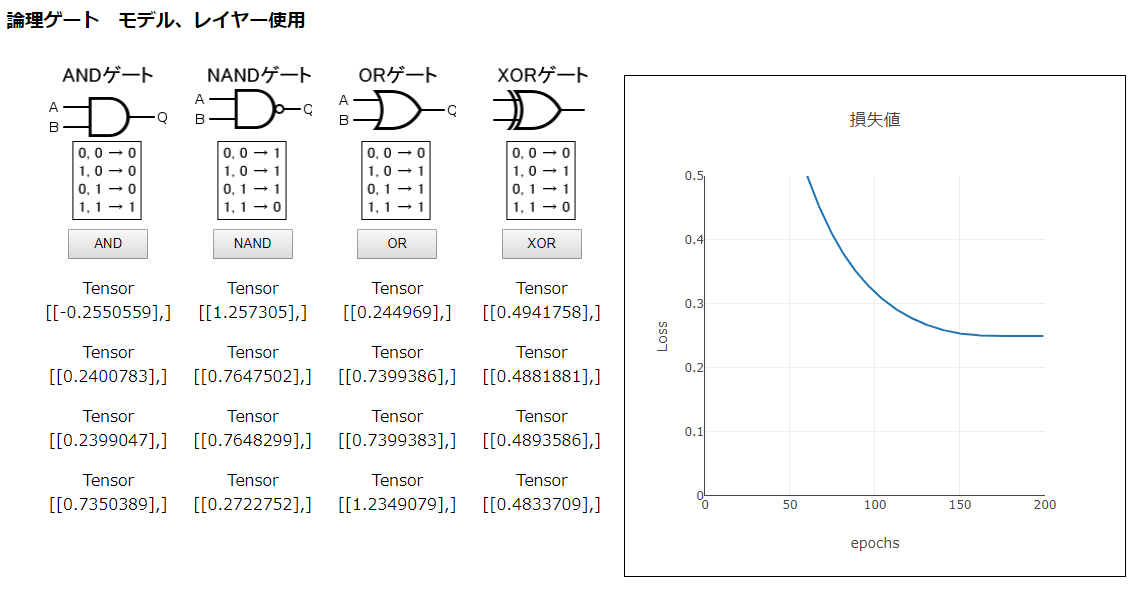
optimizerをsgdからrmspropに変え、learningRateも指定したモデルを試してみます。

const model = tf.sequential();
model.add(tf.layers.dense({units: 1, inputShape: [2]}));
const learningRate = 0.01;
const optimizer = tf.train.rmsprop(learningRate);
model.compile({ loss: 'meanSquaredError', optimizer: optimizer });

前のモデルより少し良くなった感じはします。ANDゲートやNAND、ORデートでは、それらしい推測値が出ているようにも見えます。しかし、XORゲートの結果は全然で、損失値の結果も良くありません。

とは言え、やみくもに試すのもそれはそれでよくないので、参考書やネットに当たってみます。

すると「UNDERSTANDING XOR WITH KERAS AND TENSORFLOW」というページに、次のPythonコードが書かれているのを見つけました。

model = Sequential()
model.add(Dense(16, input_dim=2, activation='relu'))
model.add(Dense(1, activation='sigmoid'))

model.compile(loss='mean_squared_error',
              optimizer='adam',
              metrics=['binary_accuracy'])

これは、TensorFlow.jsでは次のように記述できます。

const model = tf.sequential();
model.add(tf.layers.dense({units: 16, inputShape: [2], activation:'elu'}));
model.add(tf.layers.dense({ units: 1,activation:'sigmoid'}));
const learningRate = 0.01;
const optimizer = tf.train.adam(learningRate);
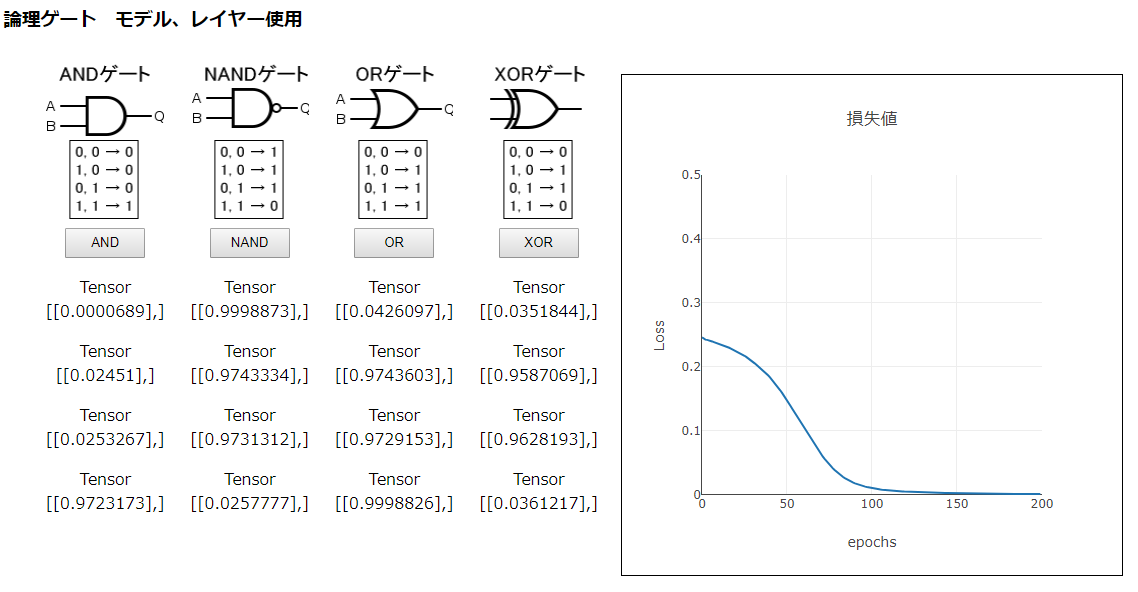
model.compile({ loss: 'meanSquaredError', optimizer: optimizer,metrics:['accuracy'] });

このモデルを試すと、次のようなかなり良好な結果が得られました。このモデルは、「4_1 TensorFlow.jsで実装した論理ゲート」のものとは異なりますが、優れたモデルのように思えます。