目次
座標
画面に描画されたシェイプすべて、座標として指定された位置を持ちます。すべての座標は、原点からの距離としてピクセル単位で計測したものです。原点[0、0]はウィンドウの左上の座標であり、右下の座標は[width-1、height-1]になります。
function setup() {
// 画面を、720ピクセル幅と400ピクセル高に設定する。
createCanvas(720, 400);
}
function draw() {
// 背景を黒に設定し、塗りをなくす
background(0);
noFill();
// 線の色を白にする
stroke(255);
// point()関数の2つのパラメータは座標を指定する。
// 1つめのパラメータはx座標で、2つめはy座標
point(width * 0.5, height * 0.5); // => (360, 200)の位置に白い点を描画
point(width * 0.5, height * 0.25); // => (360, 100)の位置に白い点を描画
// 線の色を青にする
stroke(0, 153, 255);
// 座標は点だけでなく、すべてのシェイプの描画に使用される。
// さまざまな関数のパラメータがさまざまな目的に使用される。
// たとえば、line()の最初の2つのパラメータは1つめの端点の座標を指定し、
// 2つめの2つのパラメータは2つめの端点の座標指定する。
line(0, height * 0.33, width, height * 0.33); // => (0,132)と(720, 132)を結ぶ青い線を描画
// 線の色を茶にする
stroke(255, 153, 0);
// デフォルトでは、rect()の最初の2つのパラメータは矩形の左上隅の座標、
// 2つめのペア(3つめと4つめ)は幅と高さ。
rect(width * 0.25, height * 0.1, width * 0.5, height * 0.8);
// => (180, 40)を左上隅とする、幅が360、高さが320の、線が茶色の矩形を描画
}-解説-
上記コードを実行すると、下図に示す結果が得られます。

幅と高さ
‘width’と’height’変数は、createCanvas()関数で定義された、表示ウィンドウの幅と高さの値を持ちます。
function setup() {
// 720 x 400ピクセルのキャンバスを作成
createCanvas(720, 400);
// noLoop()関数はdraw()を1度だけ実行する。
// noLoop()を呼び出さない場合には、draw()内のコードが連続して実行できる
noLoop();
}
function draw() {
// 背景色をグレーにする
background(127);
// 線はなし
noStroke();
// iは0,20,40,60と20ずつ、380まで大きくなる
for (let i = 0; i < height; i += 20) {
// print(i);
// 塗りを緑にする
fill(129, 206, 15);
// (0, i)を左上隅とする幅が720, 高さが10の横に長い矩形を描画
rect(0, i, width, 10);
// 塗りを白にする
fill(255);
// (i, 0)を左上隅とする幅が10, 高さが400の縦に長い矩形を描画
rect(i, 0, 10, height);
}
}-解説-
上記コードを実行すると、次の結果が得られます。

上記サンプルでは、キャンバスを、createCanvas(720, 400)によって、720 x 400というサイズで作成しているので、createCanvas()の呼び出し以降、widthには720、heightには400を持った変数としてアクセスできます。
おまけ:グリッド(格子模様)の作り方
上記サンプルからは、格子模様の作り方が見て取れます。格子模様は次のように、forループをもう1つ加えると描画できます。
function draw() {
// 背景色をグレーにする
background(127);
// 線はなし
noStroke();
// iは0,20,40,60と20ずつ、380まで大きくなる
for (let i = 0; i < height; i += 20) {
// 塗りを緑にする
fill(129, 206, 15);
// (0, i)を左上隅とする幅が720, 高さが10の横に長い矩形を描画
rect(0, i, width, 7);
}
for (let i = 0; i < width; i += 20) {
// 塗りは緑のまま
rect(i, 0, 7, height);
}
}
SetupとDraw
draw()関数内のコードは、上から下へ、プログラムが停止するまで、連続して実行されます。
let y = 100;
// setup()関数内のステートメントは、プログラムの開始時に1度だけ実行される。
function setup() {
// createCanvas()は必ず最初に記述する
createCanvas(400, 300);
// 線の描画カラーを白にする
stroke(255);
// フレームレートをデフォルトの半分に
frameRate(30);
}
// draw()内のステートメントは、プログラムが停止するまで実行される。
// 各ステートメントは順番に実行され、
// 最終行が読み取られた後、最初の行がまた実行される。
function draw() {
// 背景を黒に設定
background(0);
// 論理を更新 => 変数yの更新
update();
//
line(0, y, width, y);
}
// 論理を更新
function update() {
// yを1だけ小さくする
y = y - 1;
// yは際限なく小さくなるので、条件(y<0)をつけて、
// yが0より小さくなったらheight変数の値(今の場合は400)にする。
// これにより、白い線はキャンバス下端から上昇する
if (y < 0) {
y = height;
}
}おまけ:アニメーションして見える理由
上記サンプルでは、白い線が上昇し、上端を超えると下端に移ってまた上昇するという動作を繰り返しているように見えます。これはいわゆるアニメーション表現であり、ここではJavaScriptコードとp5.jsの機能によって実現されています。
白い線が上昇しているように見えるのは、本来的には人間の脳の錯覚です。draw()関数は1秒間に60回(上記サンプルでは(半分の30回)呼び出され、そのたびに、p5.jsは1ピクセルずつを上にずらして横線を描画しています。1秒間に30回という変化は人間の知覚を超えたスピードなので、残像現象によって、脳はそれが動いているものだと間違えるのです。
これについては、「1_1 アニメーションとは?」や「1=2 アニメーションが動いて見える原理」でも述べています。
おまけ:論理の更新(update())
白い線が上昇するアニメーションを表現するには、draw()関数が呼び出されるタイミングに合わせて、白い線の垂直方向のy位置を少しずつ小さくする必要があります。具体的に言うと、あるときにy位置が100であった白線を描いたら、その次のdraw()関数が呼び出されるときには、y位置を99にして白線を描く、ということです。
これは白い線が上昇するアニメーションを表現するための”理屈”で、ここではそれを”論理”と呼んでいます。論理が破綻していては、コンピュータはこちらが思ったようにアニメーションを描画してくれないので、誰がどう見ても矛盾していない理屈をコンピュータに示す必要があります。
論理はdraw()関数内に記述できますが、論理の更新は大体が変数の更新なので、専用の関数にまとめると、理屈が分かりやすくなります。上記コードで言うと、update()関数が専用の関数に当たります。そして、draw()関数ではまず、背景色を描画し、次に論理を更新して、最後に線などの描画物を描くようにします。ここで大切なのが、論理を更新してから、描画物を描くという順番です。
ループしない(noLoop())
noLoop()関数はdraw()関数を1回だけ実行させます。noLoop()を呼び出さない場合には、draw()内のコードが絶えず実行されます。
再描画(redraw())
redraw()関数はdraw()を1回だけ実行させます。次の例では、マウスがクリックされるたびにdraw()が1回実行されます。
let y;
function setup() {
createCanvas(400, 300);
stroke(255);
// draw()を1回だけ実行
noLoop();
// 変数yは高さの半分
y = height * 0.5;
}
function draw() {
background(0);
y = y - 4;
if (y < 0) {
y = height;
}
line(0, y, width, y);
}
// redraw()関数はdraw()を1回だけ実行する。
// ここではマウスクリックするたびにredraw()を呼び出しているので、
// 線が4ずつ上がっていく
function mousePressed() {
redraw();
}自分で関数が定義できる
次のdrawConcentricCircles()関数を自分で定義すると、描画したいさまざまな対象を比較的容易に描画することができます。関数を呼び出すときには、対象ごとに描画する円のx座標、y座標、最大円の直径、同心円の数を引数として与えます。
function setup() {
createCanvas(720, 400);
background(0, 149, 149);
noStroke();
// ループしない => draw()は1回だけ呼び出される
noLoop();
}
// 同心円を描く関数を呼び出す
function draw() {
drawConcentricCircles(width * 0.25, height * 0.4, 200, 4);
drawConcentricCircles(width * 0.5, height * 0.5, 300, 10);
drawConcentricCircles(width * 0.75, height * 0.3, 120, 6);
}
// 同心円を描画する
// パラメータは、描画する円のx座標、y座標、最大円の直径、同心円の数
// 円の直径が小さくなるほど色を白(255)に近くする
function drawConcentricCircles(xloc, yloc, size, num) {
// 連続して描く円の直径をいくつ減らすか
const steps = size / num;
// num値から、255を超えないグレー値を作る
const grayvalues = 255 / num;
print('grayvalues :' + grayvalues);
// 描画したい同心円の数分だけ繰り返す
for (let i = 0; i < num; i++) {
// 繰り返すごとに直径は、sizeより、steps分だけ小さくなる
const diameter = size - (i * steps);
print('i :' + i, '直径 :' + diameter);
// 繰り返すごとに塗り色は白に近づく
const val = i * grayvalues;
print('グレー値 :' + val);
fill(val);
// (xloc, yloc)を中心とする直径diameterの円を、塗り色valで描く
ellipse(xloc, yloc, diameter);
}
}
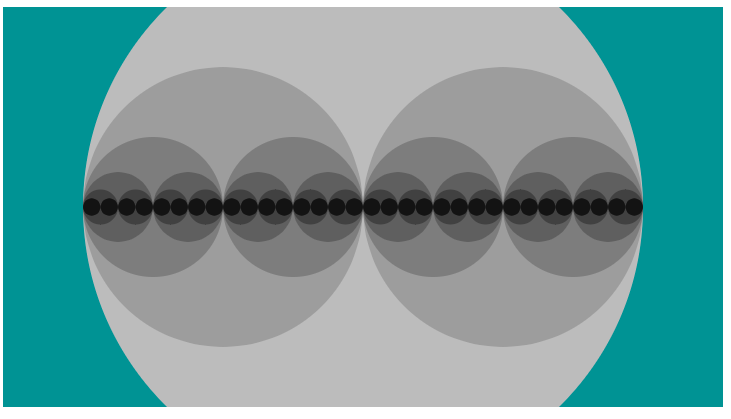
再帰
再帰のデモ。再帰とは、関数が自分自身を呼び出すことを意味します。drawCircle()関数が、自分のブロックの最後で自分自身を呼び出している点に注目してください。この自分自身への呼び出し(再帰)は、変数levelが1に等しくなるまでつづきます(参考:再帰)。
function setup() {
createCanvas(720, 400);
background(0, 149, 149);
noStroke();
noLoop();
}
function draw() {
drawCircle(width / 2, 280, 6);
}
// 再帰関数
// https://developer.mozilla.org/ja/docs/Web/JavaScript/Guide/Functions#Recursion
function drawCircle(x, radius, level) {
const tt = (126 * level) / 4.0;
fill(tt);
ellipse(x, height / 2, radius * 2, radius * 2);
// levelが1になるまで、自分自身を再度呼び出す
if (level > 1) {
level = level - 1;
drawCircle(x - radius / 2, radius / 2, level);
drawCircle(x + radius / 2, radius / 2, level);
}
}
グラフィックを作成(p5.Renderer)
新しいp5.Rendererオブジェクトを作成して返します。このクラスは、グラフィックのバッファをオフスクリーン(画面外)に描画したい場合に使用します。2つのパラメータはピクセル単位の幅と高さを定義します。
let pg;
function setup() {
createCanvas(710, 400);
// p5.Renderer
// https://p5js.org/reference/#/p5.Renderer
pg = createGraphics(400, 250);
}
function draw() {
drawBackgroud();
drawBlurredCircle();
drawOffscreenCanvas();
// オフスクリーンバッファを、image()を使って画面に描画
image(pg, 150, 75);
}
// 背景用の矩形を描く
function drawBackgroud() {
// 塗りにアルファ値を設定する(fill(gray, [alpha]))ことで、
// この上に塗る円が移動時ににじんで見えるようになる
fill(0, 12);
rect(0, 0, width, height);
// 同じ効果はこれでも可能
//background(0, 12);
}
// マウス位置に白い円を描く
function drawBlurredCircle() {
fill(255);
noStroke();
ellipse(mouseX, mouseY, 60, 60);
}
// オフスクリーンキャンバスに背景色と白い円を描く
function drawOffscreenCanvas() {
// オフスクリーンキャンバスの背景を濃いグレーに
pg.background(51);
// 塗りはなし、線を白に
pg.noFill();
pg.stroke(255);
// オフスクリーンキャンバスに白線の円を描く
pg.ellipse(mouseX - 150, mouseY - 75, 60, 60);
}-解説-
ここで行われていることは一見複雑に見えますが、draw()内の呼び出しを1つずつ確認していくと理解できます。
まず、オフスクリーンキャンバスとは、下図の赤枠で囲んだ部分の内容を描画している、画面外のキャンバスを言います。より具体的に言うと、コンピュータのメモリ内に存在するだけでそのままでは描画されないキャンバスです。このキャンバスはcreateGraphics()関数によって、上の例では400 x 250のサイズで作成されます(変数pg)。
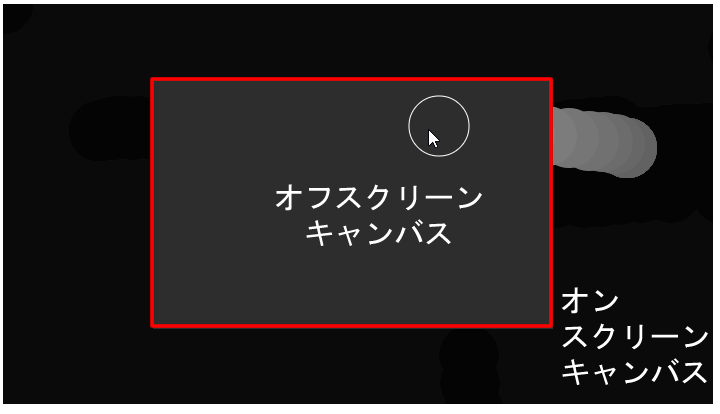
このオフスクリーンキャンバスに描画を行うのがdrawOffscreenCanvas()関数です。この関数では濃いグレーの背景の上に、白い線の円をマウス位置に描きます。
では、draw()関数内の呼び出しを1つずつ見ていきましょう。
function draw() {
drawBackgroud();
drawBlurredCircle();
drawOffscreenCanvas();
image(pg, 150, 75);
}最初に呼び出されるdrawBackgroud()関数は、背景用の黒い矩形を描画します。ここでfill()関数の第2引数にアルファ値を指定することで、この後呼び出すdrawBlurredCircle()で描画する白い円が、マウスを動かしたときににじんで描かれるようになります。
次にdrawBlurredCircle()を呼び出します。この関数では、マウス位置に白い円を描きます。ここまでのコードで、マウスににじんで追随する円が描画できます。たとえば赤い円に変えると、火の玉のような表現が可能になります。

そしてdrawOffscreenCanvas()関数を呼び出します。これは、オフスクリーンキャンバスに描画を行う関数です。createGraphics()関数で作成したp5.Rendererオブジェクトpgでは、メインのキャンバスと同様のメソッドが使用できるので、ここでは、p5.Rendererオブジェクトである変数pgを通して、オフスクリーンキャンバスに描画を行っています。
function drawOffscreenCanvas() {
// オフスクリーンキャンバスの背景を濃いグレーに
pg.background(51);
// 塗りはなし、線を白に
pg.noFill();
pg.stroke(255);
// オフスクリーンキャンバスに白線の円を描く
pg.ellipse(mouseX - 150, mouseY - 75, 60, 60);
}ただしオフスクリーンキャンバスに描いた物はこのままでは、メインのキャンバスに描画されません。この例ではimage()関数を使って、オフスクリーンキャンバスの描画物をメインのキャンバスに描いています。
image()関数のimgパラメータにはp5.Imageかp5.Elementが指定できます。createGraphics()が返すp5.Rendererオブジェクトは、”レンダラーの周りの薄いラッパー”であるp5.Graphicsオブジェクトでもあり、p5.Elementを継承しているので、image()関数に使用できます。
