８：数学(Math)

インクリメントとデクリメント

“a++”と記述することは、”a = a + 1″と同じです。”a–“と記述することは、”a = a – 1″と同じです。

let a; // 上の帯用の、1ずつ大きく(インクリメント)する変数
let b; // 下の帯用の、1ずつ小さく(デクリメント)する変数
let direction; // 方向の反転に使う変数

// 数値を表示するための<span>要素
let spanDirection;
let spanA, spanWidth_A;
let spanB, spanWidth_B;

function setup() {
    createCanvas(710, 400);
    // RGBカラーモードの値の最大値をwidth(710)に設定
    // colorMode(mode, [max])
    // これによりstroke()関数には255より大きな710までの数値が与えられるようになる。
    // その大きさは、x:255 = 0:710の比例で調整される
    // => color(711)はcolor(255)と解釈される
    colorMode(RGB, width);
    a = 0;
    b = width;
    direction = true;
    // フレームレートを30にする(通常の半分)
    frameRate(30);
    // 線の太さを2
    strokeCap(PROJECT)
    strokeWeight(2);

    // 数値を表示するための<span>要素をp5.dom.jsで作成
    spanDirection = createSpan('SPAN');
    spanDirection.position(10, 420);

    spanA = createSpan('SPAN');
    spanA.position(70, 420);
    spanWidth_A = createSpan('SPAN');
    spanWidth_A.position(130, 420);

    spanB = createSpan('SPAN');
    spanB.position(70, 450);
    spanWidth_B = createSpan('SPAN');
    spanWidth_B.position(130, 450);
}

function draw() {
    // aをインクリメント
    a++;
    // aは1ずつ大きくなる。aが幅(710)を超えたら
    if (a > width) {
        // aを0に戻す
        a = 0;
        // 方向を反転
        direction = !direction;
    }
    // 方向がtrueなら
    if (direction === true) {
        // aを線の色にする。 => aは0から1ずつ大きくなるので、黒から白に変化する
        stroke(a);
        spanA.html(a);
        spanWidth_B.html(width - b)
    }
    else {
        // 方向がtrueでないなら => aが幅より大きくなってaが0に戻った状態
        // aは0から1ずつ大きくなるので、線の色は白から黒に変化する
        stroke(width - a);
        spanWidth_A.html(width - a);
        spanB.html(b)
    }

    spanDirection.html(direction);

    // (a,0)から(a.height/2)まで線を引く => 縦線
    line(a, 0, a, height / 2);


    // bは最初710。bをデクリメント
    b--;
    // bは1ずつ小さくなる。bが0よりも小さくなったら
    if (b < 0) {
        // bをwidthに戻す
        b = width;
    }
    // 方向がtrueなら
    if (direction === true) {
        // 線の色は黒から白に変化する
        stroke(width - b);
        // 方向がtrueでないなら
    }
    else {
        // 線の色は白から黒に変化する。
        stroke(b);
    }
    line(b, height / 2 + 1, b, height);
}

メモ

上記サンプルでは、変数aとb、width – a、width – bの数値や、ブーリアン型の変数directionの値を確認するために、p5.dom.jsライブラリを使って<span>を５つ作成し使用しています。print()関数によるコンソールへの出力で事足りる場合も多くありますが、今の場合には、aとbが高速で変化するので、aやwidth – a、b、width – bの関係性を見るには、このように画面上に表示した方が分かりやすくなります。

p5.dom.jsについては、「12：キャンバスを超えて p5.dom.js JavaScript」で述べています。またcreateSpan()関数についてはここで調べることができます。

メモ

上記サンプルのsetup()関数には、次の1行が記述されています。

colorMode(RGB, width);

colorMode()はそのプログラムのカラーモードを変更する関数ですが、ここではデフォルトのRGBモードをそのまま継続しつつ、使用できるRGBAの最大値をwidth(=710)にしています。これによりfill()やstroke()関数などでwidth(=710)を指定すると、それが255として解釈されるようになります。これはmap()関数と同様の比の計算で調整されます。このプログラムでは、キャンバスの幅710一杯をつかって白から黒、黒から白に変化させたいので、255を710に対応させているわけです。

解説

インクリメントとは1ずつ加算することを言い、++で表されます(インクリメント演算子)。上記サンプルでは、a++という式によって、draw()関数が呼び出されるたびに変数aの値が1ずつ大きくなります。

次のコードは、グローバル変数aを最初0に設定し、draw()関数でインクリメントして、それをline()関数の引数に使用することで、黒い横棒が右に伸びるアニメーションを作成する例です。draw()の１回めの呼び出しではline(0, 0, 200, 0)なので、画面右端に縦線が描かれます。２回めの呼び出しではaが1大きくなるのでline(1, 0, 200, 0)となり、前の線の1ピクセル右に線が描かれます。

draw()内では、これまでの多くのサンプルのようにbackground()を呼び出していないので、前のフレームでの描画は残存します。したがってキャンバスには２本の黒い縦線が描かれることになります。draw()関数の以降の呼び出しでも、同様にline(2, 0, 200, 0)、line(3, 0, 200, 0),…が実行されるので、結果として黒い横棒が右に伸びていくアニメーションになります。

let a;

function setup() {
    createCanvas(710, 400);
    colorMode(RGB, width);
    // aは最初0
    a = 0;
}

function draw() {
    // aの値に1を加え、それをaに代入する
    a++;
    // (a,0)と(a. height/2=200)を結ぶ線を描く
    // => background()を呼び出していないので、前の描画はキャンバスに残存する。
    // その結果、黒い横棒が右に伸びていくアニメーションになる。
    line(a, 0, a, height / 2);
}

ただしこのままではaはプログラムが実行されつづける限り1ずつ大きくなっていきます。上記サンプルではa++;の後、次のifステートメントを使って、aの値がキャンバスの幅よりも大きくなったら再度aを0に戻しています。

 if (a > width) {
     // aを0に戻す
     a = 0;
     // 方向を反転
     direction = !direction;
 }

ここで面白いのがdirection = !direction;の行です。変数directionは最初trueが代入されるブーリアン型の変数で、aの値がキャンバスの幅よりも大きくなったとき、変数の値が反転します。具体的に言うと、それまでの値がtrueだった場合にはfalseに、falseだった場合にはtrueに変わります。これは論理否定演算子(!)の働きによるものです。

演算子の優先順位

式が評価される順番を明示的に指定しない場合、式は演算子の優先順位にもとづいて評価されます。たとえば、ステートメント”4+2*8″は、まず2が8に掛けられ、その結果が4に足されます。これは、”*”が”+”よりも高い順位を持っているからです。プログラムを読むときの曖昧さを避けるには、”4+(2*8)”と記述することが推奨されます。評価の順番はコード内にかっこ(())を置くことでコントロールできます。演算子の優先順位は次のサンプル内に示しています。

// 演算子の優先順位のリスト(高 -> 低)
// 乗、除、剰余算： * / %
// 加、減算： + -
// 関係： < > <= >=
// 等価： == !=
// 論理積： &&
// 論理和： ||
// 代入： = += -= *= /= %=
function setup() {
    createCanvas(710, 400);
    // 背景をほぼ黒
    background(51);
    // 塗はなし
    noFill();
    //stroke(51);

    // 線の色を赤にする
    stroke(255, 0, 0);
    // iを0から開始し、iがwidth-20(=690)未満になるまで、iを4ずつ大きくする
    for (let i = 0; i < width - 20; i += 4) {
        // 30が70に足された後、それ(100)よりiの現在値が大きいかどうかが評価される。
        // "if (i > (30 + 70)) {"に変えて確認してみる。
        // 加算演算子(+)はより大きい演算子(&gt;)よりも優先順位が高いので、
        // 30 + 70が先に計算され、その結果(100)がiとの大小比較に使用される。
        if (i > 30 + 70) {
            line(i, 0, i, 50);
        }
    }
    // 線の色を緑にする
    stroke(0, 255, 0);
    // 2は8に掛けられ(=16)、その結果が4に足される(=20)　=> rect(20, 52, 290, 48);
    rect(4 + 2 * 8, 52, 290, 48);
    // グループ化の()演算子によってまず4と2が足され(=6)、その結果が8と掛けられる
    // => rect(48, 100, 290, 49);
    rect((4 + 2) * 8, 100, 290, 49);

    // 線の色を白にする
    stroke(255, 255, 255);
    // iを0から開始し、iがwidth(=710)未満になるまで、iを2ずつ大きくする
    // 2というのはトリック。背景の黒が面積の半分残るので暗く見える
    for (let i = 0; i < width; i += 2) {
        // 関係演算子は論理演算子より優先順位が高い。
        // iが20以上でかつ50未満であるか、または、iが100以上でかつ690未満であるなら
        if ((i > 20 && i < 50) || (i > 100 && i < width - 20)) {
            // 白の縦線を引く
            line(i, 151, i, height - 1);
        }
    }
}

解説

JavaScriptにおける演算子の優先順位はMDNの「演算子の優先順位」ページで詳しく読むことができます。

距離 一次元

マウスを左右に動かすと、移動するシェイプのスピードと方向が制御できます。

let xpos1;
let xpos2;
let xpos3;
let xpos4;
let thin = 8;
let thick = 36;

function setup() {
    createCanvas(710, 400);
    noStroke();
    xpos1 = width / 2;
    xpos2 = width / 2;
    xpos3 = width / 2;
    xpos4 = width / 2;
}

function draw() {
    background(0);

    let mx = mouseX * 0.4 - width / 5.0;

    fill(102);
    rect(xpos2, 0, thick, height / 2);
    fill(204);
    rect(xpos1, 0, thin, height / 2);
    fill(102);
    rect(xpos4, height / 2, thick, height / 2);
    fill(204);
    rect(xpos3, height / 2, thin, height / 2);

    xpos1 += mx / 16;
    xpos2 += mx / 64;
    xpos3 -= mx / 16;
    xpos4 -= mx / 64;

    if (xpos1 < -thin) {
        xpos1 = width;
    }
    if (xpos1 > width) {
        xpos1 = -thin;
    }
    if (xpos2 < -thick) {
        xpos2 = width;
    }
    if (xpos2 > width) {
        xpos2 = -thick;
    }
    if (xpos3 < -thin) {
        xpos3 = width;
    }
    if (xpos3 > width) {
        xpos3 = -thin;
    }
    if (xpos4 < -thick) {
        xpos4 = width;
    }
    if (xpos4 > width) {
        xpos4 = -thick;
    }
}

解説

一次元での距離とは、同じ数直線上にある２点間の距離を言います。通常は大きい方から小さい方を引いて求めます。p5.jsのmouseXシステム変数は、キャンバスの左上隅(0, 0)からのマウスの水平方向の距離を示します。詳しくは「3_1：p5.js 変数」で述べています。

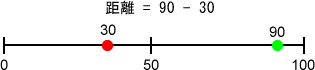
上記サンプルでは、このmouseXを利用して４つの棒が左右に動くアニメーションを実現しています。しかし、このままでは動きが少し複雑なので、上の２つに限って見ていくことにします。次のコードでは、矩形の色を赤と黄色に変えています。また関数を新たに作成し、変数名も区別変えていように変えています。

let xposThinRed; // 細い赤の縦棒のx位置用変数
let xposThickYellow; // 太い黄色の縦棒のx位置用変数
const thin = 8; // 細さは8
const thick = 36; // 太さは36

let spanMouseX; // mouseX値を画面に表示するための<span>要素
let spanMX; // 変数mx値を画面に表示するための<span>要素


function setup() {
    // キャンバスサイズは700 x 400
    createCanvas(700, 400);
    noStroke();

    // キャンバス水平方向の真ん中
    xposThinRed = width / 2;
    xposThickYellow = width / 2;

    spanMouseX = createSpan('SPAN');
    spanMouseX.position(50, 420);
    spanMX = createSpan('SPAN');
    spanMX.position(180, 420);
}

// 細い赤の縦棒を(xposThinRed,0)に描画
function drwaThinRed() {
    fill(255, 0, 0);
    rect(xposThinRed, 0, thin, height / 2);
}

// 太い黄色の縦棒を(xposThickYellow,0)描画
function drwaThckYellow() {
    fill(255, 255, 0);
    rect(xposThickYellow, 0, thick, height / 2);
}

// 論理の更新 => 位置取りに関係する変数を更新
function update() {
    // mouseXに0.4を掛けた数値から140を引いた値
    // mxの値は、マウスがセンターにあるとき0に、右端にあるときwidth/5に、左端にあるとき-width/5になる
    let mx = mouseX * 0.4 - width / 5.0;

    // mouseXとmx値を画面に表示
    spanMouseX.html('mouseX: ' + mouseX);
    spanMX.html('mx: ' + mx);

    // 細い棒と太い棒の移動量に変化を持たせる。
    // xposThinRedの方が変化量が多い => 速く移動する
    // mxは、マウス位置に合わせて、-140 -> 0 -> 140と変化するので、
    // 棒は、マウスが端にあるときほど速く、中にあるときほど遅く移動することになる。
    xposThinRed += mx / 16;
    xposThickYellow += mx / 64;

    // xposThinRedが-8より小さくなったら、700にする => 画面左端より左に行ったら右端に移動
    if (xposThinRed < -thin) {
        xposThinRed = width;
    }
    // xposThinRedが700よりも大きくなったら、-8にする => 画面右端より右に行ったら左端に移動
    if (xposThinRed > width) {
        xposThinRed = -thin;
    }
    // xposThickYellowが-36より小さくなったら、700にする => 画面左端より左に行ったら右端に移動
    if (xposThickYellow < -thick) {
        xposThickYellow = width;
    }
    // xposThickYellowが700よりも大きくなったら、-36にする => 画面右端より右に行ったら左端に移動
    if (xposThickYellow > width) {
        xposThickYellow = -thick;
    }
}

function draw() {
    background(0);
    update();
    // 細い棒の方が速く移動するので、細い棒を太い棒の前景に描いて、
    // 細い棒が太い棒の前を通過するように見せる
    drwaThckYellow();
    drwaThinRed();
}

mouseXは次の行で出てきます。これは何をしているのでしょう？

let mx = mouseX * 0.4 - width / 5.0;

このサンプルでは、マウスがキャンバスセンター辺りにあるときは、棒の移動スピードを遅く、端の方にあるときは速くする必要があります。この変数mxはそのために使用されます。

mxは次の条件を満たす変数だと想定できます。

• マウスがキャンバスセンターにあるときはゼロになる
• マウスがセンターから右に進むと大きくなり(正の数)、キャンバスの右端で最大になる
• マウスがセンターから左に進むと大きくなり(負の数)、キャンバスの左端で最大になる

これを、mxの最大値を140(=width/5)、最小値を-140(=-width/5)とすると、mouseXとの関係は下図のように表せます。

この関係を方程式で解いてみます。mouseX*x + y = mx

mouseXが0のとき、mxは-140 => 0*x + y = -140 => y = -140 => yは-140
mouseXが350のとき、mxは0 => 350*x – 140 = 0 => 350*x = 140 => x = 140/350 = 0.4 => xは0.4
mouseXが700のとき、mxは140 => 700*x -140 = 140 => 700*x = 280 => x = 280/700 = 0.4 => xは0.4

ここから、mouseX*0.4 – 140(=width/5)が見えてきます。

つづく次の２行では、求めたmxを16と64で割って、細い赤の棒と太い黄色の棒の現在位置に足しています。同じ数値(mx)を小さな数と大きな数で割るので、小さな数で割った方が結果は大きくなります。つまり細い赤の棒の方が速く移動する、ということになります。

 xposThinRed += mx / 16;
 xposThickYellow += mx / 64;

距離 二次元

マウスを動かすと、円の格子模様が見え隠れします。ここではマウスから各円までの距離を計測し、その距離に比例したサイズ(遠いほど大きい)を設定しています。

let max_distance;

function setup() {
    createCanvas(710, 400);
    noStroke();
    max_distance = dist(0, 0, width, height);
}

function draw() {
    background(0);

    for (let i = 0; i <= width; i += 20) {
        for (let j = 0; j <= height; j += 20) {
            let size = dist(mouseX, mouseY, i, j);
            size = (size / max_distance) * 66;
            ellipse(i, j, size, size);
        }
    }
}

解説

二次元での距離とは、同じ平面上にある２点間の距離を言います。平面は横向きの水平方向(X軸)と、縦向きの垂直方向(Y軸)で表されます。

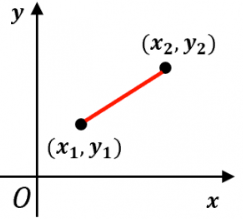
２点間の距離はdist()関数で簡単に求めることができます。dist()関数については「4_2：応答：マウスを追跡 p5.js JavaScript」で述べています。

次のコードは、ある点とマウスのある位置を線で結び、その距離を表示する簡単な例です。

let p1;

function setup() {
    createCanvas(400, 300);
    textSize(20);
    // 点(30, 60)を表すオブジェクトを作成
    p1 = {
        x: 30,
        y: 60
    };
}

function draw() {
    background(0);
    // 白線をマウスとp1の間に描く
    stroke(255);
    line(mouseX, mouseY, p1.x, p1.y);
    // 赤丸をマウスとp1の位置に描く
    noStroke();
    fill(255, 0, 0)
    ellipse(p1.x, p1.y, 10, 10);
    ellipse(mouseX, mouseY, 10, 10);

    fill(255);
    // マウスとp1間の距離を文字で描画
    const distance = dist(mouseX, mouseY, p1.x, p1.y);
    text(distance, 10, 260)
}

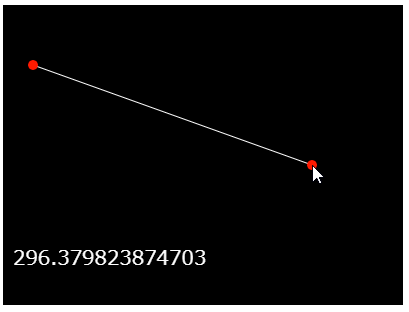
前述した、円の格子模様が見え隠れするサンプルは、一見複雑に見えますが、行われていることは単純です。キャンバスの座標を20ピクセルごとに２重のforループでその時々の座標とマウス位置との距離を調べ、近い場合は小さな、遠い場合は大きな円を描いています。キャンバスの背景は黒で、円が小さい場合は、円と円との間の黒が見えます。逆に円が大きい場合は円と円が重なり、背景の黒は見えません。円の枠線は描かれないので、このとき背景は白に見えます。

サイン

sin()関数を使って、円のサイズを滑らかに伸縮しています。

let diameter;
let angle = 0;

function setup() {
  createCanvas(710, 400);
  diameter = height - 10;
  noStroke();
  fill(255, 204, 0);
}

function draw() {
  background(0);

  let d1 = 10 + (sin(angle) * diameter) / 2 + diameter / 2;
  let d2 = 10 + (sin(angle + PI / 2) * diameter) / 2 + diameter / 2;
  let d3 = 10 + (sin(angle + PI) * diameter) / 2 + diameter / 2;

  ellipse(0, height / 2, d1, d1);
  ellipse(width / 2, height / 2, d2, d2);
  ellipse(width, height / 2, d3, d3);

  angle += 0.02;
}

解説

学生時代、数学で習った三角関数のサインやコサインは値が滑らかに周期的に変化するので、繰り返すアニメーションによく利用されます。サインとコサインと円の関係については「7_6：円運動 p5.js JavaScript」で述べています。

サイン波

次のコードは、plotly.jsのグラフ描画機能を使って、サインの波を描画します。plotly.jsについては「４：配列(Arrays)」で簡単に説明しています。

let angle = 0; // 角度　ラジアン値
const speed = 0.05; // 角速度 => 単位時間当たりに進む角度

function setup() {
    createCanvas(400, 400);
}

function draw() {
    // 変数angleは、draw()が呼び出されるたびにspeed分だけ大きくなる
    const sinValue = sin(angle);
    // サインの曲線を描画
    plot(frameCount, sinValue);
    // 1周期辺りで止める
    if (frameCount > 127) {
        noLoop();
    }
    // 角度に角速度を加える。
    // draw()関数は毎秒60回呼び出されるので、speedは1秒間に60回加算されることになる。
    angle += speed;
}

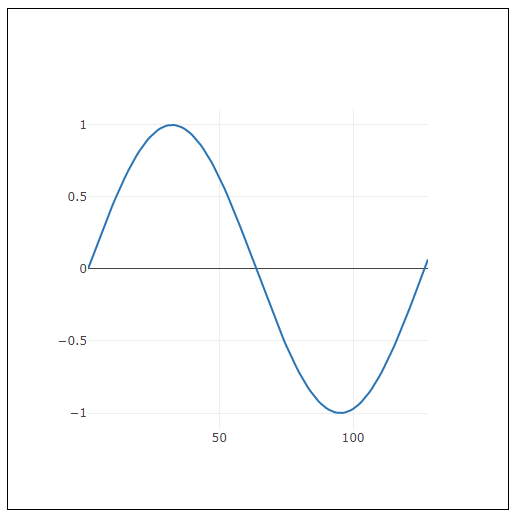
サインの値はこのように、0から始まり滑らかに増加して1になり、そこから滑らかに減って-1になり、そこから再び増加に転じます。

波の高さはサインの値に数値を掛けることで高くできます。サイン値にたとえば6を掛けると、グラフは次のように変化します。

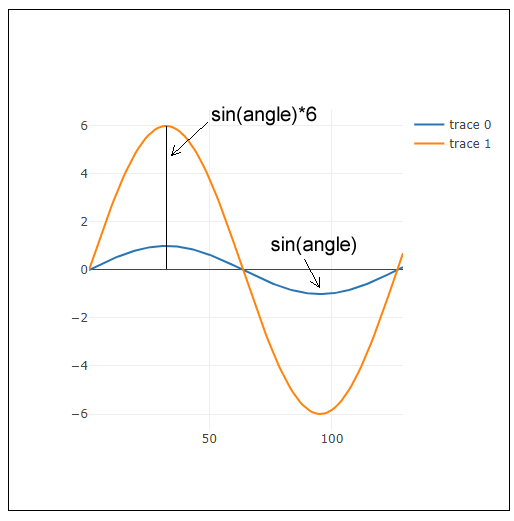
次の例では、50を代入した変数amplitudeを用意し、これにサイン値に掛けたものを円の直径に指定して円を描いています。円の直径は0から50の間で滑らかに変化するので、円のサイズが滑らかに変化するアニメーションになります。なお直径のdiameterは負の値なりますが、これはp5.jsの働きによってellipse()関数に絶対値が渡されます(「2_4：p5.js 楕円(円)、円弧を描く。度とラジアンの扱い。」を参照)。

let angle = 0;
const amplitude = 50; // 振幅
const speed = 0.05; // 角速度 => 単位時間当たりに進む角度

function setup() {
    const canvas = createCanvas(200, 200);
    // グラフの右にp5.jsのキャンバスを配置するための処置
    // https://github.com/processing/p5.js/wiki/Positioning-your-canvas
    canvas.parent('sketch-holder');
    noStroke();
    fill(255, 255, 0);
}

function draw() {
    background(204);
    const sinValue = sin(angle);
    // サイン値にamplitudeを掛ける
    const diameter = sinValue * amplitude;
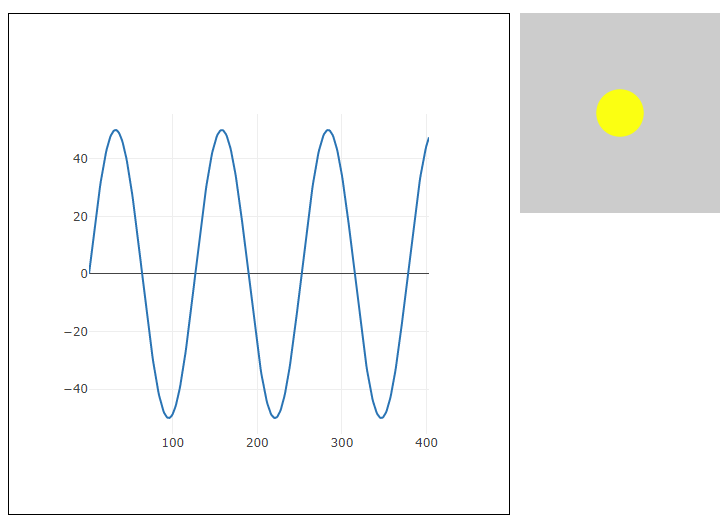
    plot(frameCount, diameter)
        //波の高さが50になる => 描く円は、直径が0から50の間で変化する
    ellipse(width / 2, 100, diameter);
    angle += speed;
}

またサイン値に数値を加えると、その数値分だけ曲線全体を上に移動させることができます。これは曲線の最小値を引き上げることになります。上の例の場合、最小値は0なので円は見えなくなりますが、適当な数値を加えることで、円の最小サイズを決めることができます。

let angle = 0;
const amplitude = 50; // 振幅
const speed = 0.05; // 角速度 => 単位時間当たりに進む角度
let isStart = false;

function setup() {
    const canvas = createCanvas(200, 200);
    // グラフの右にp5.jsのキャンバスを配置するための処置
    // https://github.com/processing/p5.js/wiki/Positioning-your-canvas
    canvas.parent('sketch-holder');
    noStroke();
    fill(255, 255, 0);

    const startButton = setButton('START', {
        x: 530,
        y: 240
    });
    startButton.mousePressed(() => {
        isStart = true;
    });

    const stopButton = setButton('STOP', {
        x: 630,
        y: 240
    });
    stopButton.mousePressed(() => {
        isStart = false;
    });

}

function draw() {
    background(204);
    if (isStart) {
        const sinValue = sin(angle);
        // サイン値にamplitudeを掛ける
        const diameter = sinValue * amplitude + 80;
        plot(frameCount, diameter)
            //波の高さが50になる => 描く円は、直径が0から50の間で変化する
        ellipse(width / 2, 100, diameter);
        angle += speed;
    }
}

function setButton(label, pos) {
    const button = createButton(label);
    button.size(80, 30);
    button.position(pos.x, pos.y);
    return button;
}

sin()関数に与える引数に手を加えると、サインの曲線をずらすことができます。これを円の描画に利用すると、大きくなり小さくなる複数の円のアニメーションのタイミングのずれが表現できます。sin()関数にはデフォルトで、ラジアン値を与えます。

let angle = 0;
const amplitude = 50; // 振幅
const speed = 0.05; // 角速度 => 単位時間当たりに進む角度

function setup() {
    createCanvas(400, 400)
    noStroke();
    fill(255, 255, 0);
}

function draw() {
    const canvas = createCanvas(400, 500);
    // https://github.com/processing/p5.js/wiki/Positioning-your-canvas
    canvas.parent('sketch-holder');
    background(204);

    // 標準のsin(angle)
    // 波の高さ(振幅)を50にし、全体を80上げる
    const diameter = sin(angle) * amplitude + 80;
    plot(frameCount, diameter);
    fill(42, 116, 180);
    // 一番上の青い円
    ellipse(width / 2, 100, diameter);

    // (angle+90度)のサイン値に振幅を掛ける => 位相(サイン波のずれ)
    const phase1 = sin(angle + PI / 2) * amplitude + 80;
    fill(255, 139, 27);
    // 真ん中のオレンジの円
    ellipse(width / 2, 250, phase1);
    addPlot2(frameCount, phase1);

    // (angle+180度)のサイン値に振幅を掛ける => 位相(サイン波のずれ)
    const phase2 = sin(angle + PI / 4) * amplitude + 80;
    fill(26, 161, 47);
    // 一番下の緑の円
    ellipse(width / 2, 400, phase2);
    addPlot3(frameCount, phase2);

    if (frameCount > 128) {
        noLoop();
    }
    angle += speed;
}

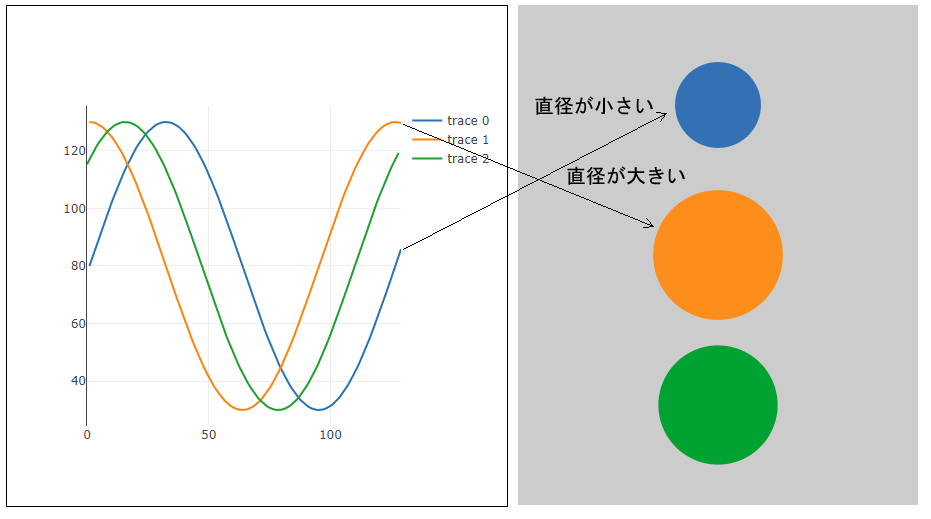
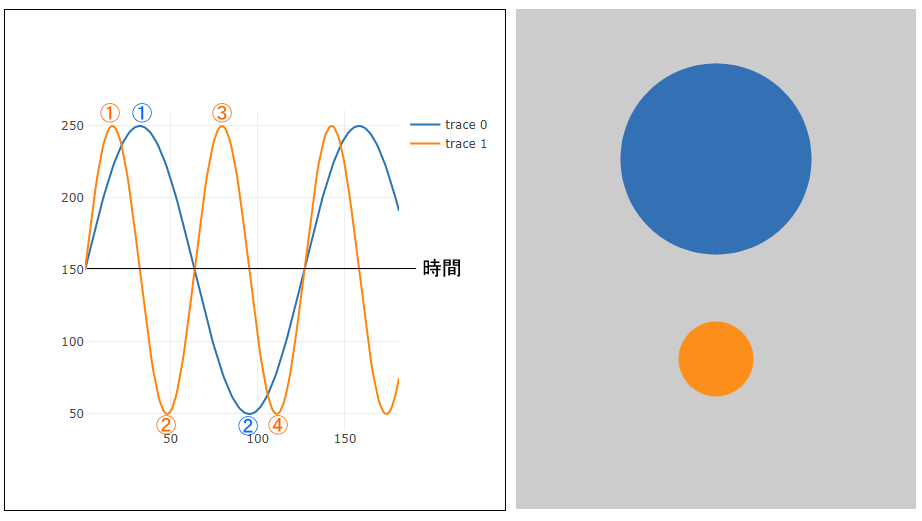
変数angleに足す変数speedの値を変えると、サイン値の１周期の長さを変えることができます。これは、心臓の鼓動にたとえると、「ドク、ドク」と鳴っていたものが「ドクドクドクドク」と速く鳴るようなものです。

let angle1 = 0;
let angle2 = 0;

const speed1 = 0.05;
const speed2 = 0.1
const amplitude = 100;

function setup() {
    const canvas = createCanvas(400, 500);
    // https://github.com/processing/p5.js/wiki/Positioning-your-canvas
    canvas.parent('sketch-holder');
    noStroke();
    fill(255, 255, 0);
}

function draw() {
    background(204);

    // trace0(青色の曲線)
    const sinValue1 = sin(angle1);
    const diameter1 = sinValue1 * amplitude + 150;
    plot(frameCount, diameter1);
    // 青い円
    fill(42, 116, 180);
    ellipse(width / 2, 150, diameter1);

    // trace1(オレンジ色の曲線)
    const sinValue2 = sin(angle2);
    diameter2 = sinValue2 * amplitude + 150;
    addPlot2(frameCount, diameter2);
    // オレンジ色の円
    fill(255, 139, 27);
    ellipse(width / 2, 350, diameter2)
    if (frameCount > 180) {
        noLoop();
    }
    angle1 += speed1;
    angle2 += speed2;
}

サイン、コサイン

sin()とcos()関数を使った線形運動のサンプル。sin()とcos()は、0からPI*2(TWP_PI,約6.28度)までの数値を受け取り、-1から1までの数値を返します。この値を拡大するとより大きな運動を生み出すことができます。

次のコードは、分かりやすくするため、関数にまとめるなど、p5.jsのコードから少し変更しています。

let angle1 = 0;
let angle2 = 0;

const speed1 = 2;
const speed2 = 3;

let sinY1, sinY2;
let cosX1, cosX2;

let halfWidth, halfHeight;

let leftX, rightX;
let topY, bottomY;

const amplitude = 70;
const diameter = 70;

function setup() {
    createCanvas(710, 400);

    halfWidth = width / 2;
    halfHeight = height / 2;

    leftX = halfWidth - 120;
    rightX = halfWidth + 120;

    topY = halfHeight - 120;
    bottomY = halfHeight + 120;

    noStroke();
    rectMode(CENTER);
}

// 変数を更新
function update() {
    //  angle1のサイン値とコサイン値を計算
    sinY1 = sin(radians(angle1)) * amplitude + halfHeight;
    cosX1 = cos(radians(angle1)) * amplitude + halfWidth;

    // angle2のサイン値とコサイン値を計算
    sinY2 = sin(radians(angle2)) * amplitude + halfHeight;
    cosX2 = cos(radians(angle2)) * amplitude + halfWidth;

    angle1 += speed1;
    angle2 += speed2;
}

function draw() {
    background(0);
    update();

    // 真ん中の白く矩形を描画
    fill(255);
    rect(width / 2, height / 2, 140, 140);

    // 上下に動く黄色の円を描画
    fill(255, 204, 0);
    ellipse(leftX, sinY1, diameter);
    ellipse(rightX, sinY2, diameter);

    // 左右にに動く円を描画
    fill(0, 102, 153);
    ellipse(cosX1, topY, diameter);
    ellipse(cosX2, bottomY, diameter);
}

解説

コサインの値も-1から1の間の滑らかな曲線を描きますが、始まりが1であることがサインと異なります。0からスタートしたい多くのアニメーションではcos()ではなくsin()が使用されます。とはいえ、cos(angle)はsin(angle + PI / 2)と同等なので、この意味において大きな違いはないとも言えます。

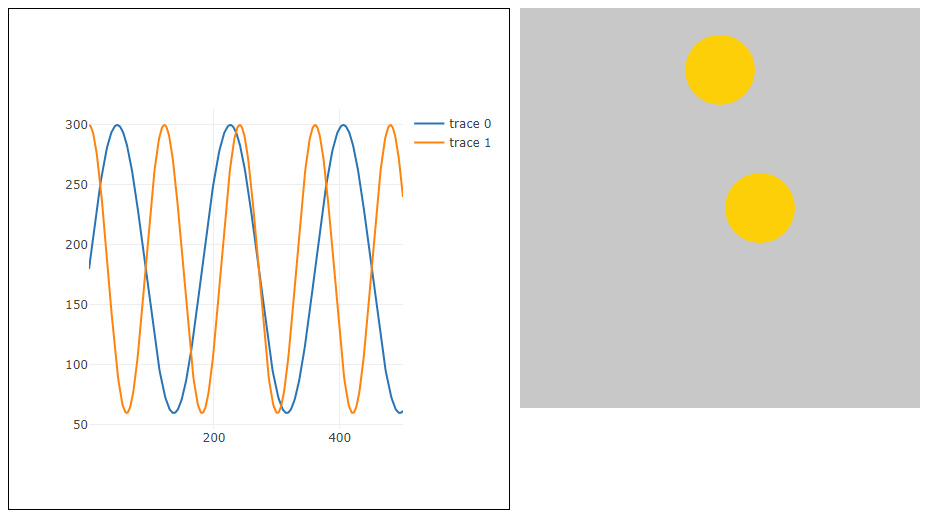
次のコードは、左右に動く円と上下に動く円のアニメーションの基本的なコードです。上下に動くか左右に動くかはellipse()関数の引数に何を与えるかで決まります。

let angle1 = 0;
let angle2 = 0;
const speed1 = 2;
const speed2 = 3;
let sinY1;
let cosX1;

const amplitude = 120;
const diameter = 70;

function setup() {
    const canvas = createCanvas(400, 400);
    canvas.parent('sketch-holder');
    noStroke();
    rectMode(CENTER);
}

function update() {
    // angle1のサイン値を計算
    // sinY1は180からスタートし、-> 300 -> 60 -> 300の滑らかな変化を繰り返す
    sinY1 = sin(radians(angle1)) * amplitude + 180;
    plot(frameCount, sinY1);
    // cosX1は380からスタートし、-> 60 -> 300 -> 60の滑らかな変化を繰り返す
    // angle2にはspeed2を加えるので、cosX1の曲線の周期は、sinY1の周期より短い
    cosX1 = cos(radians(angle2)) * amplitude + 180;
    addPlot2(frameCount, cosX1);
    // 上下に動く円と左右に動く円のスピードは異なることになる
    angle1 += speed1;
    angle2 += speed2;

    if (frameCount > 500) {
        noLoop();
    }
}

function draw() {
    background(200);
    update();
    fill(255, 204, 0);
    // x位置は固定、y位置が180 -> 300 -> 60 -> 300...と変化するので、その結果円が上下に動くアニメーションになる。
    ellipse(width / 2, sinY1, diameter);
    // y位置は固定、x位置が300 -> 60 -> 300...と変化するので、その結果円が左右に動くアニメーションになる。
    ellipse(cosX1, height / 2, diameter);
}

サイン波

単純なサイン波をレンダリングします。オリジナルはダニエルシフマン。

const xspacing = 16; // 水平方向での円同士の距離
let theta = 0.0; // 開始角度は0
const angularVelocity = 0.02; // 角速度
const amplitude = 75.0; // 波の高さ(振幅)
const period = 500.0; // 波を繰り返すまでのピクセル数
let dx; // xの増分
let yvalues; // 波の高さを保持する配列

function setup() {
    createCanvas(710, 400);
    // 波全体の横幅を726にする
    const waveWidth = width + 16;
    dx = (PI * 2 / period) * xspacing;
    // floor(waveWidth / xspacing)は45 => new Array(45) => 要素数が45の配列が作成される
    // Array コンストラクタに 0 から 232-1 までの間の整数値 1 個が与えられた場合、その数値の要素数を持つ新しい JavaScript 配列が生成されます
    // https://developer.mozilla.org/ja/docs/Web/JavaScript/Reference/Global_Objects/Array
    yvalues = new Array(floor(waveWidth / xspacing));

    noStroke();
    fill(255);
    noLoop();
}

function draw() {
    background(0);
    update();
    for (let x = 0; x < yvalues.length; x++) {
        ellipse(x * xspacing, height / 2 + yvalues[x], 16, 16);
    }
}

function update() {
    // 角度を0.02だけ大きくする
    theta += angularVelocity;
    // 現時点のx(theta)について、sin()関数でy値を求める
    let x = theta;
    for (let i = 0; i < yvalues.length; i++) {
        yvalues[i] = sin(x) * amplitude;
        x += dx;
    }
}

解説

このサンプルは、単にサイン波を描画しているのではなく、数珠つながりに見える円をサイン波に沿って動かす、というものです。具体的にいうと、１回の描画で使用するサイン値をキャンバスの幅分ほど用意し、それをy値として、適切なx値と合わせて位置(x,y)に、毎フレーム、円を描画します。

このサンプルのコードは洗練されていて理解しづらいので、以降に段階を追って見ていくことにします。

サイン波の基本概念

本格的に述べようとすると物理の難しい話になるので、以下では基本的な概念を見ていきます。物理学的な波については「わかりやすい高校物理の部屋」の「単振動」などが参考になるかと思います。

「7_6：円運動 p5.js JavaScript」で示したようなコードを記述すると、半径aの円周上を移動する赤丸のアニメーションと、変化しつづけるサインの波を描画することができます。

下図のグラフの横軸はp5.jsのframeCountプロパティ値、つまり時間で、縦軸は半径*sin(角度)、つまり増幅したサイン値です。半径の値はサイン波のグラフでは、波の高さ(振幅)に当たります。

右の円周上の赤丸は0度の位置からスタートし時計回りに移動して、やがて円を１周しますが、これは周期と呼ばれます。左のグラフで言うと、(0, 0)からスタートして上に進み、振幅値を境に下降し、y値0を過ぎて、マイナスの振幅値で上昇に転じて、y値0に戻るまでに当たります。

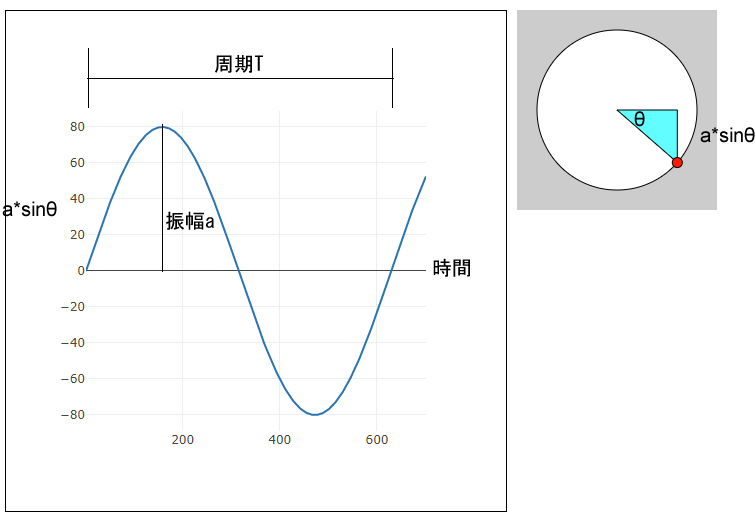
右の円の赤丸は１フレーム進むと、次の位置に進みます。このとき前の位置と次の位置との間に生まれる角度は角速度と呼ばれます。「7_6：円運動 p5.js JavaScript」のコードでは、draw()関数内で、angle += speed を記述していますが、この変数speedが角速度に当たります。

角速度は、進んだ角度を単位時間で割ることで計算できます。角速度(ω) = 角度(θ) / 時間(t)
赤丸は円を１周するのに周期の時間かかるので、この関係は、角速度(ω) = 360度(PI * 2) / 周期(T) でも表すことができます。

数珠つながりの円を描画する

ではいったん、サイン波から離れ、数珠つながりの円を描画する方法を見ていきます。

// キャンバス一杯に数珠つながりで並ぶ円を描く

const xspacing = 16; // 水平方向での円の中心同士の間隔
let yvalues; // 波の高さを保持する配列
let period; // 波全体の幅 => 周期

function setup() {
    createCanvas(710, 400);
    // 周期はキャンバス幅よりxspacing分大きくする => 円の並びは波形になるので、幅より長くして、切れて見えないようにする
    period = width + xspacing;
    // floor(period / xspacing)は45 => new Array(45) => 要素数が45の配列が作成される
    // Array コンストラクタに 0 から 232-1 までの間の整数値 1 個が与えられた場合、その数値の要素数を持つ新しい JavaScript 配列が生成されます
    // https://developer.mozilla.org/ja/docs/Web/JavaScript/Reference/Global_Objects/Array
    yvalues = new Array(floor(period / xspacing));

    // yvalues配列の値として暫定的に1を与えておく
    for (let i = 0; i < yvalues.length; i++) {
        yvalues[i] = 1;
    }

    noStroke();
    fill(255);
    noLoop();
}

function draw() {
    background(0);
    // yvaluesの長さ(45)だけ繰り返す
    for (let x = 0; x < yvalues.length; x++) {
        // print(x * xspacing); // => 0,16,32,48,...704まで
        ellipse(x * xspacing, height / 2 + yvalues[x], 16, 16);
    }
}

円はdraw()関数内で、ellipse(x * xspacing, height / 2 + yvalues[x], 16, 16) によって描かれます。変数xspacingは0,16,32,48
と16刻みで704まで変化するので、順に横並びになります。ここでのポイントは配列のyvalues変数です。これは、setup()内の次のコードで作成されます。

yvalues = new Array(floor(period / xspacing));

xspacingは16、periodはwidth + xspacingなので、710 + 16 = 726です。726/16は45.375でfloor()関数によって端数が切り捨てられ、new Array()には45が渡されます。このnew Array()はp5.jsの関数ではなくJavaScript本体のコンストラクタで、new Array()に整数を与えると、その数分を要素数とする空の配列が作成できます。今の場合は、要素数が45個の配列が作成され、変数yvaluesに割り当てられます。空の配列とはこんなものです。[,,,,,,,…]。

上記コードでは、setup()内のforループで、yvalues[i] = 1 を実行して、この配列に数値の1を45個入れているので、円はキャンバスの高さから1引いた高さに描画されることになります。

円をサイン波の形状に並べて描く

並べる要素(円)が描けたので、円をサイン波の形状に並べる方法を見ていきます。これは、sin()関数を使って適切な値をyvalues配列に入れていく、ということです。

// yvalues配列に適切な値を入れる

const xspacing = 16;
let yvalues;
let period;

const amplitude = 75; // 振幅

function setup() {
    createCanvas(710, 400);
    period = width + xspacing;
    yvalues = new Array(floor(period / xspacing));

    // yvalues配列に値を入れる
    for (let i = 0; i < yvalues.length; i++) {
        // 角速度を計算する => 角速度 = 円の一周(160度) / 周期 => 180度/726
        const angularVelocity = TWO_PI / period;
        // print(angularVelocity);   // 0.008654525216500808
        // print(degrees(angularVelocity)) //0.4958677685950414度

        // 角度は角速度*その時の時間。今の場合はxspacingも掛ける
        const x = angularVelocity * i * xspacing;
        // sin(x)に振幅を掛ける
        const y = sin(x) * amplitude;
        yvalues[i] = y;
    }

    noStroke();
    fill(255);
    noLoop();
}

function draw() {
    background(0);
    for (let x = 0; x < yvalues.length; x++) {
        ellipse(x * xspacing, height / 2 + yvalues[x], 16, 16);
    }
}

変数amplitudeは振幅で、a*sinθのaに当たる変数です。yvalues配列には、setup()内で次のようにして値を入れています。

// yvalues配列に値を入れる
for (let i = 0; i < yvalues.length; i++) {
    // 角速度を計算する => 角速度 = 円の一周(160度) / 周期 => 180度/726
    const angularVelocity = TWO_PI / period;

    // 角度は角速度*その時の時間。今の場合はxspacingも掛ける
    const x = angularVelocity * i * xspacing;
    // sin(x)に振幅を掛ける
    const y = sin(x) * amplitude;
    yvalues[i] = y;
}

変数angularVelocityは角速度で、前述した「角速度(ω) = 360度(PI * 2) / 周期(T)」の方法で求めています。 TWO_PIは360度を意味するp5.jsの定数です。変数periodはキャンバスの幅よりもxspacingだけ大きい、サイン波をキャンバス一杯に描くための周期と見なせます。参考までにangularVelocityの数値を調べてみると、ラジアン単位で 0.0086、度単位で0.4958ほどです。

次いでangularVelocityにiとxspacingを掛けて変数xに代入しています。sin()関数に与えたい角度は角速度にそのときの時間を掛けたものです。forループの変数iは時間を掛けて繰り返される中で値が1ずつ大きくなるので、時間と見なすことができます。また今の場合は、瞬間瞬間のサイン波を描くのではなく、ある時間内(周期)でのサイン値をまとめて１度に描くので、時間変化を取り込む必要があります。

これをx値としてsin()関数に与え、それに振幅を掛けた結果をy値としてyvalues配列のi番めの値として指定します。実に賢い方法です。

アニメーションさせる

円をサイン波の形状に並べることができたので、後はこれを動かします。そのためには、setup()内に記述したyvalues配列に値を入れるforループを取り出し、draw()から呼び出すようにします。ただし今の場合必要なのは一瞬一瞬のサイン値なので、forループの変数(i)は掛けません。

// 波を動かす

const xspacing = 16;
let yvalues;
let period;

const amplitude = 75;

let angularVelocity; // 角速度
let theta = 0.0; // sin()に適用する角度

function setup() {
    createCanvas(710, 400);
    period = width + xspacing;
    yvalues = new Array(floor(period / xspacing));

    // 角速度を求める
    angularVelocity = TWO_PI / period;

    noStroke();
    fill(255);

    frameRate(30);
    //noLoop();
}

// '今'の1フレーム
function update() {
    for (let i = 0; i < yvalues.length; i++) {
        // 今の1フレームなので時間のiは掛けない
        theta += angularVelocity * xspacing;
        const y = sin(theta) * amplitude;
        yvalues[i] = y;
    }
}

function draw() {
    background(0);
    update();
    for (let x = 0; x < yvalues.length; x++) {
        ellipse(x * xspacing, height / 2 + yvalues[x], 16, 16);
    }
}

波の足し合わせ

２つの波を足し合わせることで、より複雑な波が作成できます。オリジナルはダニエルシフマン。

let xspacing = 8; // 水平方向の位置間の距離
let w; // 波全体としての幅
let maxwaves = 4; // 足し合わせる波の合計

let theta = 0.0;
let amplitude = new Array(maxwaves); // 波の高さ
// Xをインクリメントする値。
// periodとxspacingの機能として計算される。
let dx = new Array(maxwaves);
// 波の高さの値の保持に使用する配列
let yvalues;

function setup() {
    createCanvas(710, 400);
    frameRate(30);
    colorMode(RGB, 255, 255, 255, 100);
    // 波全体の幅はキャンバスの幅よりxspacing*2分大きくする
    w = width + 16;

    // 各波の振幅と角速度を求め、配列に入れる
    for (let i = 0; i < maxwaves; i++) {
        // 振幅
        amplitude[i] = random(10, 30);
        let period = random(100, 300); // 波が繰り返すまでのピクセル数 => 個々の波の周期
        // 角速度(ここでxspacingを掛けておくと、後で掛ける必要がなくなる)
        dx[i] = (TWO_PI / period) * xspacing;
    }
    // y値の配列、要素数付き(90個)
    yvalues = new Array(floor(w / xspacing));
}

function draw() {
    background(0);
    calcWave();
    renderWave();
}

function calcWave() {
    // 角度に0.02(角速度)を足す
    theta += 0.02;

    // すべての高さをいったん0に設定
    for (let i = 0; i < yvalues.length; i++) {
        yvalues[i] = 0;
    }

    // 波の高さの値を積算する
    // y値は積算され、波のよって適用される関数が変わるので、
    // 波の高さに変化が生まれる
    for (let j = 0; j < maxwaves; j++) {
        // 変数xはforループの繰り返し中のみ有効
        let x = theta;
        for (let i = 0; i < yvalues.length; i++) {
            // この波にはsin()を適用
            if (j % 2 === 0) {
                yvalues[i] += sin(x) * amplitude[j] - 100;
                // この波にはcos()を適用
            }
            else {
                yvalues[i] += cos(x) * amplitude[j] + 50;
            }
            // xに波ごとの角速度を足す
            x += dx[j];
        }
    }
}

function renderWave() {
    noStroke();
    fill(255, 50);
    ellipseMode(CENTER);
    for (let x = 0; x < yvalues.length; x++) {
        ellipse(x * xspacing, width / 2 + yvalues[x], 16, 16);
    }
}

解説

ダニエル　シフマンオリジナルによるこのサンプルも非常に複雑に思えますが、元のアイデアはただ１つ、波の高さを表す数値の配列を用意し、そこにsin()とcos()を別々に適用し積算することで、複雑に変化する複数の波を作り出す、というものです。

下図の左は通常のサイン波です。その時点でのsin(x) * amplitudeを描くのでそれを=演算子でy値に代入します。下図の右は、これを+=演算子を使ってy値に積算しています。これにより波の形に変化が現れます。

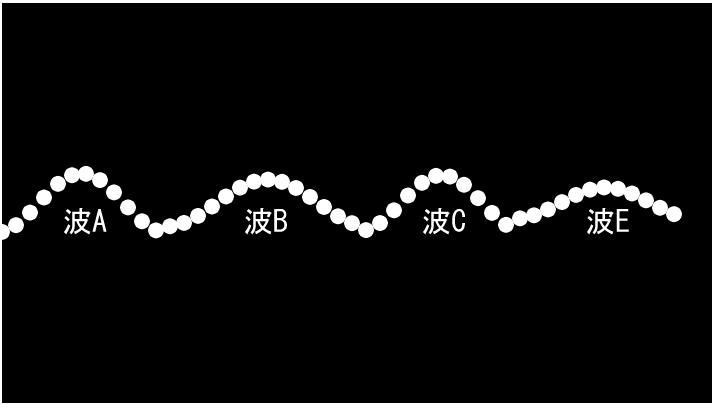
そうではなく、実際に４つの波の計算を行い、それをつなぎ合わせようとしたのが次の例です。波ごとに周期や振幅、角速度を計算し、各配列に収めて、最後にそれらを連結して、値を円のy値として描画します。

// 複数の波を足す

const xspacing = 14;

let yvaluesA; // 波Aのy値を入れる配列
let yvaluesB; // 波Bのy値を入れる配列
let yvaluesC; // 波Cのy値を入れる配列
let yvaluesD; // 波Dのy値を入れる配列

let yvalues; //

let periodA; // 波Aの周期
let periodB; // 波Bの周期
let periodC; // 波Cの周期
let periodE; // 波Eの周期

let angularVelocityA; // 波Aの角速度
let angularVelocityB; // 波Bの角速度
let angularVelocityC; // 波Cの角速度
let angularVelocityD; // 波Dの角速度

let angle = 0.0;

function setup() {
    createCanvas(710, 400);

    // 波の周期をランダムに決める
    periodA = random(100, 300);
    periodB = random(100, 300);
    periodC = random(100, 300);
    periodD = random(100, 300);


    // 波の振幅をランダムに決める
    amplitudeA = random(10, 30);
    amplitudeB = random(10, 30);
    amplitudeC = random(10, 30);
    amplitudeD = random(10, 30);

    //  波のy値を入れる配列、要素数つき
    yvaluesA = new Array(floor(periodA / xspacing));
    yvaluesB = new Array(floor(periodB / xspacing));
    yvaluesC = new Array(floor(periodC / xspacing));
    yvaluesD = new Array(floor(periodD / xspacing));

    // 波の角速度を求める
    angularVelocityA = TWO_PI / periodA;
    angularVelocityB = TWO_PI / periodB;
    angularVelocityC = TWO_PI / periodC;
    angularVelocityD = TWO_PI / periodD;

    noStroke();
    frameRate(20);
}

// '今'の1フレーム
function update() {
    // ２つの波に共通して適用する角度
    angle += 0.02;

    yvaluesA = getYvaluesArray(yvaluesA, angle, angularVelocityA, amplitudeA);
    yvaluesB = getYvaluesArray(yvaluesB, angle, angularVelocityB, amplitudeB);
    yvaluesC = getYvaluesArray(yvaluesC, angle, angularVelocityC, amplitudeC);
    yvaluesD = getYvaluesArray(yvaluesD, angle, angularVelocityD, amplitudeD);

    // 値の入った波Aと波Bの配列を１つの配列にまとめる
    yvalues = yvaluesA.concat(yvaluesB).concat(yvaluesC).concat(yvaluesD);
}

function getYvaluesArray(arr, theta, angularVelocity, amplitude) {
    for (let i = 0; i < arr.length; i++) {
        // 角度に波Aの角速度を足す
        theta += angularVelocity * xspacing;
        // その角度のサイン値を求め振幅を掛けてy値とする
        arr[i] = sin(theta) * amplitude;
    }
    return arr;
}

function draw() {
    background(0);
    update();
    for (let x = 0; x < yvalues.length; x++) {
        ellipse(x * xspacing, height / 2 + yvalues[x], 16, 16);
    }
}

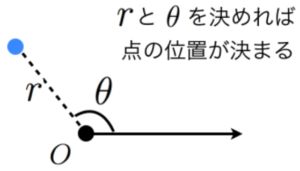
極座標から直交座標への変換

極座標(r,theta)を直交座標(x, y)に変換します。つまり、
x = rcos(theta)
y = rsin(theta)
です。オリジナルはダニエルシフマン。

// 極座標から直交座標への変換
// 座標を距離と角度(r, theta)で表す

let r; // 距離

let theta; // 角度
let theta_vel; // 角速度
let theta_acc; // 角速度

function setup() {
    createCanvas(710, 400);

    // 値を初期化
    r = height * 0.45;
    theta = 0;
    theta_vel = 0;
    theta_acc = 0.0001;

    ellipseMode(CENTER);
    noStroke();
    fill(200);
}

function draw() {
    background(0);

    // 原点を画面センターに移動
    translate(width / 2, height / 2);

    // 極座標から直交座標へ変換
    let x = r * cos(theta);
    let y = r * sin(theta);

    // 得られた(x, y)位置に円を描く
    ellipse(x, y, 32, 32);

    // (この例では距離rは一定で変化しない)
    // 角速度に加速度を足す
    theta_vel += theta_acc;
    // 角度に角速度を足す
    theta += theta_vel;
}

解説

「直交座標と極座標（２次元）の変換とメリットの比較」によると、

平面上の点の位置は，二つの数字を使うことで表現できます。例えば，直交座標（xy 直交座標，デカルト座標）では (x,y) で点の位置を表します。一方，極座標では (r,θ) で点の位置を表します。

ただし

• r は原点からの距離を表し，動径と呼ばれます。
• θ は始線（原点を通る基準の半直線，x 軸の正の向きと一致させるのが慣例）から反時計周りに測った角度を表し，偏角と呼ばれます。

とあります。

つまり距離rと角度thetaが分かれば、点(x, y)が分かる、ということです。上記サンプルでは、次のコードがこれに当たります。

// 極座標から直交座標へ変換
let x = r * cos(theta);
let y = r * sin(theta);

rを目先の行先までの距離と考えると、１フレーム後の移動先が角度と距離から計算できます。この場合rは1フレーム当たりの移動距離、つまりスピードと考えることができます。

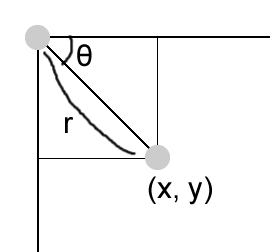
draw()関数でこの計算を行い、その(x, y)位置に円を描くと、円がその角度の方向に移動するアニメーションが作成できます。

let posX = 0; // 円の現在位置
let posY = 0;
let theta = 45; //角度は45度

let theta_vel = 0; // 角速度
let theta_acc = 0.001; // 加速度

function setup() {
    createCanvas(300, 300);
    noStroke();
}

function update() {
    // このフレーム内での行先(vx, vy)
    const vx = cos(radians(theta)) * theta_vel;
    const vy = sin(radians(theta)) * theta_vel;
    // 現在位置に加算
    posX += vx;
    posY += vy;
    // スピードアップ
    theta_vel += theta_acc;

    if (posX > 300) {
        posX = 0;
        posY = 0;
    }
}

function draw() {
    background(150);
    update();
    // 現在位置に円を描画
    ellipse(posX, posY, 10, 10);
}

アークタンジェント

マウスを動かすと、目が見ている方向が変わります。atan2()関数は、目からカーソルへの角度を算出します。

Eye.js

class Eye {
    constructor(tx, ty, ts) {
            this.x = tx;
            this.y = ty;
            this.size = ts;
            this.angle = 0;
        }
        // mouseX, mouseY
    update(mx, my) {
        this.angle = atan2(my - this.y, mx - this.x);
    }

    display() {
        // 変換が及ぶ範囲をこのオブジェクトに限定する
        push();
        // 自身の位置を(0, 0)にする
        translate(this.x, this.y);
        // 塗りを白に(白目の部分)
        fill(255);
        // (0, 0)に、sizeを直径とする円を描く
        ellipse(0, 0, this.size);
        // angle分だけ回転
        rotate(this.angle);
        // 塗りを黄緑に
        fill(153, 204, 0);
        // (sizeの1/4, 0)に、sizeの半分を直径とする円を描く
        ellipse(this.size / 4, 0, this.size / 2, this.size / 2);
        pop();
    }
}

sketch.js

let e1, e2, e3;

function setup() {
    createCanvas(720, 400);
    noStroke();
    // Eye(x, y, size)
    e1 = new Eye(250, 16, 120);
    e2 = new Eye(164, 185, 80);
    e3 = new Eye(420, 230, 220);
}

function draw() {
    background(102);
    e1.update(mouseX, mouseY);
    e2.update(mouseX, mouseY);
    e3.update(mouseX, mouseY);
    e1.display();
    e2.display();
    e3.display();
}

線形補間

マウスを移動させると、白丸が少し遅れてマウスに追随します。アニメーションを描画するフレームとフレームの間で、円は、lerp()関数を使って、現在位置からカーソルに向かってその時点の距離の一部(0.05)だけ移動します。これは、lerp()だけによるイージング効果と言えます。

let x = 0;
let y = 0;

function setup() {
    createCanvas(720, 400);
    noStroke();
}

function draw() {
    background(51);

    // lerp()は、特定の増分で２つの数値間の数値を計算する。amtパラメータは、２つの値を
    // 補間する量。0.0は最初の点に等しく、0.1は最初の点に非常に近い。0.5は２つの値の
    // ちょうど中間になる。

    // ここではamtに0.05を指定しているので、マウス位置までの距離の5%分、毎フレーム、移動する。
    x = lerp(x, mouseX, 0.05);
    y = lerp(y, mouseY, 0.05);

    ellipse(x, y, 50, 50);
}

解説

lerp()関数の働きを次の簡単な例で見てみましょう。

const a = 30;
const b = 230;
const y = 50;
stroke(255, 0, 0);
// 補間に使う２点を赤で描画
point(a, y);
point(b, y);

// 補間量0.2 => cはaに近くなる
const c = lerp(a, b, 0.2);
stroke(0, 255, 0);
point(c, y);

// 補間量0.5 => dはaとｂの中間になる
const d = lerp(a, b, 0.5);
stroke(0, 0, 255);
point(d, y);

// 補間量0.8 => eはbに近くなる
const e = lerp(a, b, 0.8);
stroke(255, 255, 0);
point(e, y);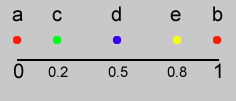

lerp()

説明

特定の増分で２つの数値間の数値を計算する。amtパラメータは、２つの値を補間する量。0.0は最初の点に等しく、0.1は最初の点に非常に近い。0.5は２つの値のちょうど中間で、1.0は２つめの点に等しくなる。amt値が1.0より大きいか0.0未満の場合には、与えられた２つの数値の比率で計算される。lerp()関数は、直線パスに沿ったモーションの作成や点線の描画に便利。

シンタックス

lerp(start, stop, amt)

パラメータ

start 数値: 最初の値
stop 数値: ２つめの値
amt 数値: 数値

ダブルランダム

２つのrandom()呼び出しとpoint()関数を使用すると、不規則なのこぎり状の線が作成できます。オリジナルはイラ・グリーンバーグ。

let totalPts = 300;
let steps = totalPts + 1;

function setup() {
    createCanvas(710, 400);
    stroke(255);
    frameRate(1);
}

function draw() {
    background(0);
    let rand = 0;
    for (let i = 1; i < steps; i++) {
        point((width / steps) * i, height / 2 + random(-rand, rand));
        rand += random(-5, 5);
    }
}

解説

このサンプルのポイントは次のforループにあります。変数randは最初0で、これがforループに入ると、random(-rand, rand)とrand += random(-5, 5)で２回処理されます。

let rand = 0;
for (let i = 1; i < steps; i++) {
    point((width / steps) * i, height / 2 + random(-rand, rand));
    rand += random(-5, 5);
}

random(-rand, rand)は-randからrand未満までのランダムな浮動小数点数を返し、rand += random(-5, 5)は、-5から5未満までのランダムな浮動小数点数をrandに足します。これがsteps(300)回繰り返されます。これによりrandは次第に大きくそして小さくなると予想できます。

下図はrandom(-rand, rand)が返す値とrand += random(-5, 5)のrandの値を、iを横軸にグラフにした一例です。randはこのように、0を中心として扇型状に正と負を激しく変化する値になるものと予想できます。もちろんrandはランダムな値なので、すべてがこうなるわけではありませんが、この正と負の激しい変化が”のこぎり状”(ギザギザ)の結果をもたらすのだと思われます。

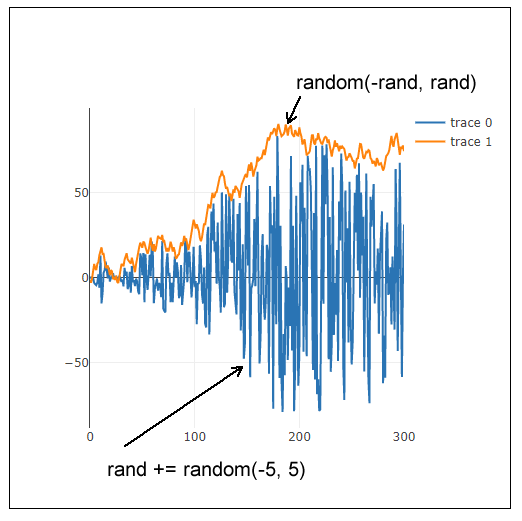
ランダム

次のイメージの基本はランダムな数値によるものです。プログラムがロードされるたびに結果は変わります。

function setup() {
    createCanvas(710, 400);
    strokeWeight(20);
    frameRate(2);
}

function draw() {
    for (let i = 0; i < width; i++) {
        // 0以上255未満のランダムな浮動小数点数
        let r = random(255);
        // 線の色をrにする
        stroke(r);
        // 太い縦線を描く
        line(i, 0, i, height);
    }
}

1Dノイズ

1Dのパーリンノイズを使って位置を決めます。

let xoff = 0.0;
const xincrement = 0.01;

function setup() {
    canvas = createCanvas(710, 400);
    background(0);
    noStroke();
}

function draw() {
    // 円をにじませる効果
    // アルファをブレンドした背景を作成
    fill(0, 10);
    // キャンバス一杯の矩形を描画
    rect(0, 0, width, height);

    // ノイズの代わりにこの行を試す
    // let n = random(0, width);

    // xoffにもとづいてノイズ値を取得し、キャンバスの幅に応じて拡大する
    let n = noise(xoff) * width;

    // 各サイクルで、xoffをインクリメントする(0.01ずつ大きくなる)
    xoff += xincrement;

    // パーリンノイズの生み出した位置に円を描く
    fill(200);
    ellipse(n, height / 2, 64, 64);
}

解説

パーリンノイズとは、ウィキペディアによると、

コンピュータグラフィックスのリアリティを増すために使われるテクスチャ作成技法。擬似乱数的な見た目であるが、同時に細部のスケール感が一定である。このため制御が容易であり、各種スケールのパーリンノイズを数式に入力することで多彩なテクスチャを表現できる。パーリンノイズによるテクスチャは、CGIで自然な外観を物に与えるためによく使われる。

とあります。

自然にあるものは単純そうに見えて実は複雑で、しかし全体として調和がとれているように見えます。たとえば石の表面をコンピュータで再現しようと、ただランダムに模様をこしらえてもそれらしく見えません。パーリンノイズはこれの解決に利用できる計算方法です。

上記はパーリンノイズで変化するのがX軸方向のみの一次元でのサンプルです。下図の左は上記サンプルのn = noise(xoff) * widthをグラフ化した例で、右は n = random(0, width)の例です。

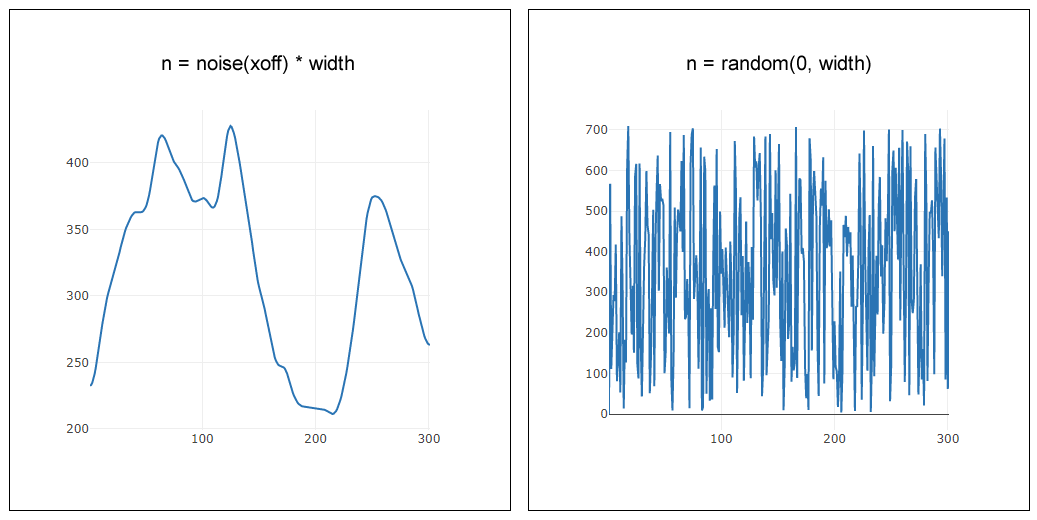
左は右と比べ、はるかに滑らかに変化しているのが分かります。また上がり方や下がり方、山のでき方に一定のパターンはないように見えます(たとえばサイン波などは一定のパターンそのものです)。この変化を利用すると、たとえば小さな虫が左右に移動する自然な動きが再現できる、というわけです。

noise()

説明

指定された座標でパーリンノイズ値を返す。パーリンノイズは、標準的なrandom()関数より順序が自然で、調和のとれた数値の連続を生み出すランダムシーケンスジェネレーター。1980年代にケン・パーリンによって考案され、以来、手続き型テクスチャ、自然なモーションや形状、地形を作成するグラフィックアプリケーションで使用されている。

random()関数との大きな違いは、座標の各ペアが１つの固定された準ランダムな値(プログラムの存続する間のみ固定される。noiseSeed()関数を参照)に対応する無限のn次元空間に、パーリンノイズが定義されているということにある。p5.jsでは、与えられた座標の数に応じて、1D、2D、3Dのノイズが計算できる。結果の値はつねに0.0から1.0になる。ノイズ値は、上記サンプルで示すように、ノイズ空間を通してアニメーションできる。２次元と３次元はまた時間として解釈できる。

実際のノイズは、この関数の周波数の使用方法の点で、音声信号の構造と似ている。パーリンノイズは、物理の音響学の概念と同様、複数のオクターブに渡って計算され、加算されて最終結果となる。

得られた結果の特性を調整する別の方法に、入力座標の拡大縮小がある。この関数は無限空間で動作するので、問題になるのは座標の値ではなく、座標間の距離(たとえば、ループ内でnoise()を使用するときなど)。一般的には、座標間の距離が小さいほど、結果のノイズシーケンスは滑らかになる。0.005から0.03の刻み値がほとんどのアプリケーションにとって最適だが、用途によって異なる。

シンタックス

noise(x, [y], [z])

パラメータ

x 数値: ノイズ空間のX座標
y 数値: ノイズ空間のy座標(オプション)
z 数値: ノイズ空間のz座標(オプション)

戻り値

数値:指定された座標でのパーリンノイズ値(0と1の間)

ノイズの波

パーリンノイズを使って、波のようなパターンを生成します。オリジナルはダニエル　シフマン。

let yoff = 0.0; // パーリンノイズの２つめの次元

function setup() {
    canvas = createCanvas(710, 400);
}

function draw() {
    background(51);
    fill(255);

    // 波の点から多角形を描画する
    beginShape();
    let xoff = 0; // オプション１：2D ノイズ
    //let xoff = yoff; // オプション２：1Dノイズ

    // 水平方向のピクセル(キャンバスの幅)分だけ、10飛ばしで繰り返す
    for (let x = 0; x <= width; x += 10) {
        // Calculate a y value according to noise, map to
        // xoffとyoffで、X軸方向とY軸方向の２次元のノイズを生成
        const n = noise(xoff, yoff);

        // 0-1のノイズを200-300にマッピング
        // オプション１：2Dノイズ => 縦横の変化 => 動いている波に見える
        const y = map(n, 0, 1, 200, 300);

        //  オプション２：1Dノイズ  => 横の変化 => 動いている波の瞬間に見える
        //const y = map(noise(xoff), 0, 1, 200, 300);

        //  オプション３：1Dノイズ  => 縦の変化 => 水位の変化に見える
        //const y = map(noise(yoff), 0, 1, 200, 300);

        // 頂点を設定
        vertex(x, y);
        // ノイズのx次元(横方向)をインクリメント
        xoff += 0.05;
    }
    // ノイズのy次元(縦方向)をインクリメント
    yoff += 0.01;
    // キャンバス右下隅と左下隅の頂点を加えて、多角形を描く
    vertex(width, height);
    vertex(0, height);
    endShape(CLOSE);
}

2Dノイズ

異なるパラメータで2Dノイズを作成します。

let noiseVal;
let noiseScale = 0.02;

function setup() {
    createCanvas(640, 360);
}

function draw() {
    background(0);
    // イメージの左半分を描画
    for (let y = 0; y < height - 30; y++) {
        for (let x = 0; x < width / 2; x++) {
            // ピクセルのオクターブ数と減衰値を設定
            noiseDetail(2, 0.2);
            noiseVal = noise((mouseX + x) * noiseScale, (mouseY + y) * noiseScale);
            stroke(noiseVal * 255);
            point(x, y);
        }
    }
    // イメージの右半分を描画
    for (let y = 0; y < height - 30; y++) {
        for (let x = width / 2; x < width; x++) {
            // ピクセルのオクターブ数と減衰値を、左半分と異なる値で設定
            noiseDetail(5, 0.5);
            noiseVal = noise((mouseX + x) * noiseScale, (mouseY + y) * noiseScale);
            stroke(noiseVal * 255);
            point(x, y);
        }
    }
    // ２つのイメージの詳細を示す
    textSize(18);
    fill(255, 255, 255);
    text('Noice2D with 2 octaves and 0.2 falloff', 10, 350);
    text('Noice2D with 1 octaves and 0.7 falloff', 330, 350);
}

解説

このサンプルはコンピュータの負担が大きいので、マウスの移動による描画結果の変化をともなわない次のコードで見ていきます。

function setup() {
    createCanvas(320, 320);
}

function draw() {
    background(0);
    // いろいろ変えてみる
    const noiseScale = 0.02;
    // const noiseScale = 0.5;
    // const noiseScale = 0.1;
    // ピクセルのオクターブ数と減衰値を設定
    noiseDetail(2, 0.2);
    //noiseDetail(5, 0.5);

    // キャンバスの全ピクセルに対して点を描く
    for (let y = 0; y < height; y++) {
        for (let x = 0; x < width; x++) {
            const noiseVal = noise(x * noiseScale, y * noiseScale);
            //const noiseVal = noise(x * noiseScale, x * noiseScale);     // 縦向きの縞模様
            //const noiseVal = noise(y * noiseScale, y * noiseScale);       // 横向きの縞模様

            stroke(noiseVal * 255); // ノイズ値をグレー値に変換してそれを線の色にする
            point(x, y); // 点を描画
        }
    }
}

下図の左はnoiseDetail(2, 0.2);を、右はnoiseDetail(5, 0.5);を呼び出した結果です。

ここで行っているのは、基本的にキャンバスの全ピクセルに対する点の描画です。点を描画する前には、stroke()関数を使って、点のグレーの度合いを設定しています。このときstroke()関数に渡しているのが、noise()関数が作成したノイズ値です。ノイズ値に255を掛けると255より小さな値になるので、グレー値として使用できます。

forループでキャンバスの全ピクセルの位置(x, y)に対してnoise()関数を適用する前、noiseDetail()関数を呼び出しています。この関数には、オクターブ数(作成するノイズの波の数)と減衰要因となる数値を指定します。

noiseScaleはnoise()関数に渡すxとyに掛ける変数です。下図はその例で、左は0.1、右は0.5のnoiseScaleを使用しています。

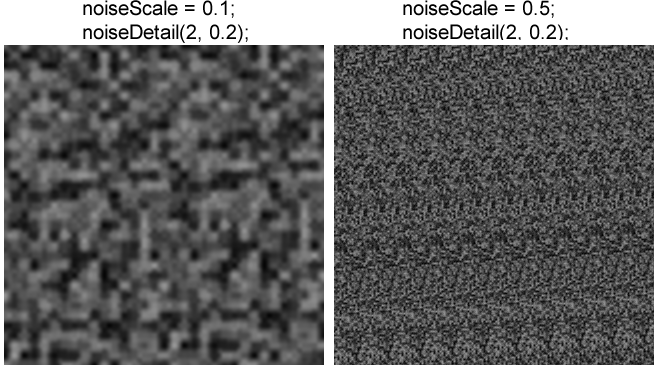
noiseDetail()関数はp5.jsのリファレンスに次のように書かれています。

noiseDetail()

説明

パーリンノイズ関数が生成する詳細な特性とレベルを調整する。物理の音響学と同様に、ノイズも複数のオクターブに渡って計算される。低いオクターブほど出力信号に大きく影響するので、ノイズの全体的な強さを決めることになる。これに対し、高いオクターブは、きめ細やかなノイズシーケンスの詳細を作り出す。

デフォルトで、ノイズは４オクターブに渡って計算され、最初のオクターブが50%の強度からスタートし、以降のオクターブは前のオクターブの半分の影響を受ける。この減衰(falloff)量は、関数パラメータを追加することで変更できる。たとえば、0.75の減衰要因は、各オクターブが、前のより低いオクターブの75%の影響(25%の減)を受けることを意味する。値は0.0から1.0の間であればどんな値でも有効だが、0.5より大きな値は、noise()関数が返す1.0より大きくなるかも知れない点に注意が必要。

これらのパラメータを変更することで、noise()関数が作成する信号は、非常に特殊な要求や特性を満たすよう調整することができる。

シンタックス

noiseDetail(lod, falloff)

パラメータ

lod 数値: ノイズに使用するオクターブの数
falloff 数値: 各オクターブの減衰要因

noise()とnoiseDetail()が行っていること

以上を踏まえて、noise()とnoiseDetail()関数が行っていることをまとめると、次のようになります(参考：「Perlin ノイズ」)。

パーリンノイズは複数のノイズの波を合成して作成される。noise()関数ではデフォルトで、４つの波が使用される。
ノイズの波の周波数は２のべき乗で増加する。周波数が２倍高い音は１オクターブ上の音なので、ここからノイズの波はオクターブと呼ばれている。noiseDetail()の第１引数に指定するのは、このオクターブの数。

波は上位に行くほど、振幅が小さくなる。これはnoiseDetail()の第２引数に指定する減衰要因が作用する。小さいほどなだらかな、きつくないノイズになる。ノイズのなだらかさはオクターブの数でも調整できる。

ランダムな弦

円のランダムな弦を重ねて描きます。弦は半透明でそれが重なり合うので、影付きの球体の錯覚が生まれます。Anders Hoffに触発されたAatish Bhatiaが寄せたサンプル。

function setup() {
    createCanvas(400, 400);
    background(255);

    // アルファ値を指定して線を半透明にする
    stroke(0, 0, 0, 15);
}

function draw() {
    // 各フレームで２つ、ランダムな弦を描く
    randomChord();
    randomChord();
}

function randomChord() {
    // 円周上のランダムな点を見つける
    let angle1 = random(0, 2 * PI);
    let xpos1 = 200 + 200 * cos(angle1);
    let ypos1 = 200 + 200 * sin(angle1);

    // 円周上にもう１つ、ランダムな点を見つける
    let angle2 = random(0, 2 * PI);
    let xpos2 = 200 + 200 * cos(angle2);
    let ypos2 = 200 + 200 * sin(angle2);

    // ２つの点を結ぶ線を描く
    line(xpos1, ypos1, xpos2, ypos2);
}

白い背景に、筋の入った円が浮かび上がり、この筋が模様になって円全体が濃くなっていきます。

解説

これは、半透明の線を時間の経過とともに重ねるというアイデアと、その線を円の弦にする、というアイデアが秀逸なサンプルで、プログラムの仕組みそのものは難しいものではありません。

弦とは、下図の点Aと点Bを結んだ線を言います。弦は、円周上の２点と、その２点と円の中心を結んでできる角度(中心角)が分かれば、引くことができます。

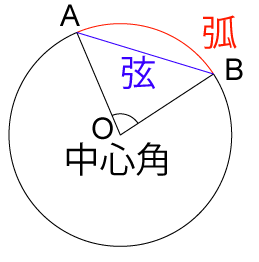
(centerX, centerY)を中心とする半径がradiusの円の上にある点(x, y)は次の計算で求めることができます(「7_6：円運動 p5.js JavaScript」を参照)。

// 円周上のx座標値
const x = centerX + cosValue * radius;
// 円周上のy座標値
const y = centerY + sinValue * radius;

次のコードは、サンプルと同じ400 x 400のキャンバスに半径200の円を描いて、その円周上のランダムな２点を求め、弦を描きます。

function setup() {
    // キャンバスのサイズは400 x 400
    createCanvas(400, 400);
    background(200);

    // キャンバス一杯の円を描く
    // 円の中心は(width/2, height/2)、半径は200
    const centerX = width / 2;
    const centerY = height / 2;
    const radius = 200;
    ellipse(centerX, centerY, radius * 2);

    // ランダムな角度を得る
    const angle1 = random(0, 2 * PI);
    // 円周上のランダムな角度にある点(xpos1, ypos1)を求める
    const xpos1 = centerX + cos(angle1) * radius;
    const ypos1 = centerY + sin(angle1) * radius;

    // 同じことをもう一度
    const angle2 = random(0, 2 * PI);
    const xpos2 = centerX + cos(angle2) * radius;
    const ypos2 = centerY + sin(angle2) * radius;

    // 求めた２点と円の中心から成る三角形を描く
    triangle(xpos1, ypos1, centerX, centerY, xpos2, ypos2);

    // 求めた２点を赤と黄色の円で描く
    fill(255, 0, 0);
    ellipse(xpos1, ypos1, 10, 10);
    fill(255, 255, 0);
    ellipse(xpos2, ypos2, 10, 10);

    // ２点を太い線で結ぶ => 弦
    strokeWeight(3);
    line(xpos1, ypos1, xpos2, ypos2);
}

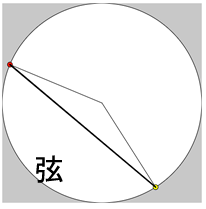
サンプルでは、randomChord()関数でこれと同様のことを行い、draw()関数で始終呼び出しているだけです。

マッピング

map()関数を使うと、任意の数値を取って、それを、今作業中のプロジェクトにより便利な新しい数値にスケーリングすることができます。たとえば、マウス位置の数値を使って、シェイプのサイズやカラーの制御に使用します。次のサンプルでは、マウスのx座標(0と360の間の数値)が、円のカラーとサイズを決める新しい数値にスケーリングしています。

function setup() {
    createCanvas(640, 400);
    noStroke();
}

function draw() {
    background(0);
    // 0から640までのmouseX値を、0と175の範囲にマッピング(対応付け)する。
    let c = map(mouseX, 0, width, 0, 175);
    // 0から640までのmouseX値を、40と300の範囲にマッピングする。
    let d = map(mouseX, 0, width, 40, 300);
    fill(255, c, 0);
    ellipse(width / 2, height / 2, d, d);
}

解説

map()関数については、「4_7：マッピング(対応付け) p5.js JavaScript」で述べています。map()関数は簡単に言うと、aとbの間で変化する数値(変数)は、cとdの間に置き換えるといくつに相当するか、を計算して返します。