p5.jsサンプルの「Simulate」項の解説として、このページでは、「ソフトボディ」、「煙のパーティクル」、「ブラウン運動」、「ばねのチェーン」、「雪の華(スノーフレーク)」、「ペンローズ・タイル」、「再帰的に枝分かれする木」、「マンデルブロ集合」、「コッホ曲線」のサンプルを解説しています。
目次
ソフトボディ
Ira Greenbergによるオリジナルサンプル。curveVertex()とcurveTightness()関数を使ったソフトボディダイナミクスシミュレーション。
// センターポイント
let centerX = 0.0,
centerY = 0.0;
let radius = 45,
rotAngle = -90;
let accelX = 0.0,
accelY = 0.0;
let deltaX = 0.0,
deltaY = 0.0;
let springing = 0.0009,
damping = 0.98;
// コーナーノード
let nodes = 5;
// ゼロフィル配列
let nodeStartX = [];
let nodeStartY = [];
let nodeX = [];
let nodeY = [];
let angle = [];
let frequency = [];
// ソフトボディダイナミクス
let organicConstant = 1.0;
function setup() {
createCanvas(710, 400);
// キャンバスのセンター
centerX = width / 2;
centerY = height / 2;
// 配列を0に初期化
for (let i = 0; i < nodes; i++) {
nodeStartX[i] = 0;
nodeStartY[i] = 0;
nodeY[i] = 0;
nodeY[i] = 0;
angle[i] = 0;
}
// コーナーノードの周波数を初期化
for (let i = 0; i < nodes; i++) {
frequency[i] = random(5, 12);
}
noStroke();
frameRate(30);
}
function draw() {
// 背景を透かす
fill(0, 100);
rect(0, 0, width, height);
drawShape();
moveShape();
}
function drawShape() {
// ノードの開始位置を計算
for (let i = 0; i < nodes; i++) {
nodeStartX[i] = centerX + cos(radians(rotAngle)) * radius;
nodeStartY[i] = centerY + sin(radians(rotAngle)) * radius;
rotAngle += 360.0 / nodes;
}
// ポリゴンを描画
curveTightness(organicConstant);
fill(255);
beginShape();
for (let i = 0; i < nodes; i++) {
curveVertex(nodeX[i], nodeY[i]);
}
for (let i = 0; i < nodes - 1; i++) {
curveVertex(nodeX[i], nodeY[i]);
}
endShape(CLOSE);
}
function moveShape() {
// センターポイントを移動
deltaX = mouseX - centerX;
deltaY = mouseY - centerY;
// ばね効果を作成
deltaX *= springing;
deltaY *= springing;
accelX += deltaX;
accelY += deltaY;
// 描画物のセンターを移動
centerX += accelX;
centerY += accelY;
// ばね効果を抑制
accelX *= damping;
accelY *= damping;
// 曲線の緊張度を変更
organicConstant = 1 - ((abs(accelX) + abs(accelY)) * 0.1);
// ノードに変化を食わる
for (let i = 0; i < nodes; i++) {
nodeX[i] = nodeStartX[i] + sin(radians(angle[i])) * (accelX * 2);
nodeY[i] = nodeStartY[i] + sin(radians(angle[i])) * (accelY * 2);
angle[i] += frequency[i];
}
}ソフトボディ(弾性体)がマウスに追随して移動し、変形します。下の実行画面写真のクリックでサンプルが開きます。
解説
これも、相当難度の高いサンプルです。コード自体は長くはないのですが、何が行われているのか、一見して理解できる方は相当な知識の持ち主でしょう。以降では、少しずつ分けて見ていきます。
まず、「ソフトボディダイナミクスシミュレーション」という言葉です。”soft body”は日本語で「弾性体」と訳され、変形するオブジェクトを意味します。たとえば、風に揺れるカーテンのシミュレーションのカーテンはソフトボディです。弾性体の反対は「剛体」で、リジッドボディ(rigid body)と呼ばれます。”ダイナミクス”とは、物体の運動を物理法則によって行うことを言います。
下の画像は、Blenderというフリーの3DCGツールで作成された、落ちる水が地面で跳ね返るCGです(「Blender Fluid Dynamics (HD)」)。この場合、ソフトボディは水で、落ちる水の速度や角度、地面との跳ね返りの強さなど、多くの物理法則が適用されていると思われます。、

サンプルコードの概略
上記サンプルでは、次のようなことが行われています。
- 配列nodeStartXとnodeStartYにキャンバスのxとy値を入れる
- その数値に変化を与え、nodeXとnodeYに入れる
- nodeXとnodeYの数値を使って、curveTightness()とcurveVertex()で曲線を描く
この変化がソフトボディに見える効果を生み出しています。
nodeStartXとnodeStartY
nodeStartXとnodeStartYは配列で、キャンバスに描画するシェイプの、開始時のx値とy値を持ちます。node(ノード)とは線と線の結び目を表す言葉で、今の場合には描くシェイプの頂点の集まりと考えられます。
次のコードは、nodeStartXとnodeStartYに一体何の数値が入るのかを確認するためのもので、実際に描画します。
const nodes = 5 // 角(コーナー)の数
// 5つのコーナーノードの開始点を含む配列
const nodeStartX = [],
nodeStartY = [];
const radius = 45; // 円の半径
let rotAngle = -90; // 回転角
let centerX, centerY; // 描画物のセンターポイント
function setup() {
createCanvas(710, 400);
// 暫定的に背景を薄いグレーに
background(200);
// キャンバスセンターをセンターポイントにする
centerX = width / 2;
centerY = height / 2;
// ノードの開始位置を計算
// => nodeStartXとnodeStartYには、centerXとcenterYを中心とする半径radiusの
// 円周上にある、5つの点の座標値が入る。点を結ぶと正五角形になる。
for (let i = 0; i < 5; i++) {
nodeStartX[i] = centerX + cos(radians(rotAngle)) * radius;
nodeStartY[i] = centerY + sin(radians(rotAngle)) * radius;
rotAngle += 360.0 / nodes;
}
// centerXとcenterYを中心とする半径radiusの円を描画
ellipse(centerX, centerY, radius * 2);
// 最初の2つの点の位置を小さな赤と緑の円で示す
fill(255, 0, 0);
ellipse(nodeStartX[0], nodeStartY[0], 8);
fill(0, 255, 0);
ellipse(nodeStartX[1], nodeStartY[1], 8);
// 5点を線で結ぶ
for (let i = 0; i < 5; i++) {
line(nodeStartX[i], nodeStartY[i], nodeStartX[i + 1], nodeStartY[i + 1]);
}
// 最後の点と最初の点を結ぶ
line(nodeStartX[4], nodeStartY[4], nodeStartX[0], nodeStartY[0]);
}下図はその実行結果です。
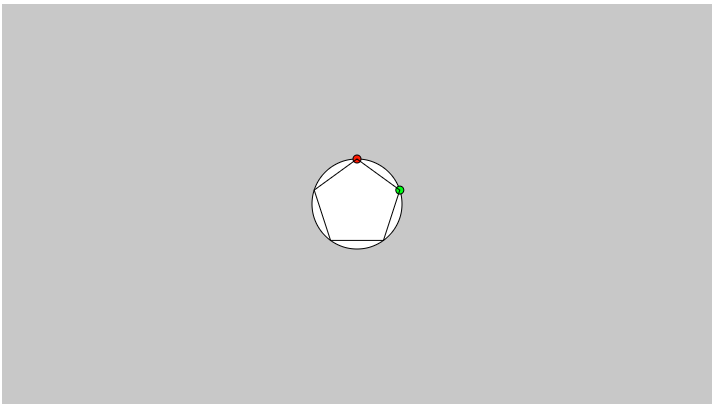
結果から言うと、nodeStartXとnodeStartYには、上図で示す五角形の頂点のxとy座標がそれぞれ入ります。これは次のコードで行われます。
// ノードの開始位置を計算
// => nodeStartXとnodeStartYには、centerXとcenterYを中心とする半径radiusの
// 円周上にある、5つの点の座標値が入る。点を結ぶと正五角形になる。
for (let i = 0; i < 5; i++) {
nodeStartX[i] = centerX + cos(radians(rotAngle)) * radius;
nodeStartY[i] = centerY + sin(radians(rotAngle)) * radius;
rotAngle += 360.0 / nodes;
}sin()とcos()関数が使われている行は、円周上の座標値を求めるコードです(「7_6:円運動 p5.js JavaScript」参照)。初期値が-90のrotAngleに、360.0 / nodes = 72度を加えることで、centerXとcenterYを中心とする半径radiusの円周上の点が5個得られます。これをnodeStartXとnodeStartYに入れています。
nodeXとnodeYの数値を毎フレーム、描画する
nodeStartXとnodeStartYに含まれる数値が分かったので、次はサンプルのmoveShape()関数に記述されている、nodeXとnodeYへの値を割り当てを追加して、nodeXとnodeYの数値を描画してみましょう。
// nodeXとnodeYの数値を毎フレーム、描画する
const nodes = 5
const nodeStartX = [],
nodeStartY = [];
const radius = 45;
let rotAngle = -90;
let centerX, centerY;
// 5つのコーナーノードのx値とy値を含む配列。描画に使用
const nodeX = [],
nodeY = [];
// 微小な変化を与える角度を含む配列
const angle = [];
// 微小な変化をもたらす周波数(揺れ具合を表す)
const frequency = [];
function setup() {
createCanvas(710, 400);
centerX = width / 2;
centerY = height / 2;
// 初期化
init();
}
function init() {
// initialize arrays to 0
// 各配列の要素を全部0にする
// nodeXとnodeY、angle配列で必要
for (let i = 0; i < nodes; i++) {
nodeStartX[i] = 0;
nodeStartY[i] = 0;
nodeX[i] = 0;
nodeY[i] = 0;
angle[i] = 0;
}
// コーナーノードの周波数(変化量)を初期化
for (let i = 0; i < nodes; i++) {
frequency[i] = random(5, 12);
}
}
function draw() {
background(200);
drawShape();
moveShape();
}
// シェイプを描画
function drawShape() {
for (let i = 0; i < 5; i++) {
nodeStartX[i] = centerX + cos(radians(rotAngle)) * radius;
nodeStartY[i] = centerY + sin(radians(rotAngle)) * radius;
rotAngle += 360.0 / nodes;
}
drawCurveVertex();
}
// コーナーノードの値を少しだけ変える
function moveShape() {
// nodeXとnodeYには、微小に変化する数値が入る
for (let i = 0; i < nodes; i++) {
nodeX[i] = nodeStartX[i] + sin(radians(angle[i]));
nodeY[i] = nodeStartY[i] + sin(radians(angle[i]));
// frequency配列にはランダムな数値が入っているので、
// angle配列に含まれる数値も変化する。
// これがsin()に渡され、微小に変化する数値が生まれる
angle[i] += frequency[i];
}
}
// curveVertex()関数を使って、Catmull-Rom(キャットムル-ロム)スプラインの
// 曲線で結んで描く。
// nodeXとnodeYの数値は微小に変化しているので、
// 描画物は揺らいでいるように見える
function drawCurveVertex() {
fill(255);
beginShape();
for (let i = 0; i < nodes; i++) {
curveVertex(nodeX[i], nodeY[i]);
}
for (let i = 0; i < nodes - 1; i++) {
curveVertex(nodeX[i], nodeY[i]);
}
endShape(CLOSE);
}以下はその結果です。曲線で描かれた丸みを帯びた白いシェイプが揺らいでいるように見えます。
draw()関数から毎フレーム呼び出されるdrawShape()関数ではnodeStartXとnodeStartY配列が供給され、そこから呼び出しているdrawCurveVertex()関数では、curveVertex()関数を使って、Catmull-Romスプラインと呼ばれる曲線を描いています。nodeStartXとnodeStartYの数値に少しの変化を与えているのは、draw()関数からこの後呼び出されているmoveShape()関数です。
// コーナーノードの値を少しだけ変える
function moveShape() {
// nodeXとnodeYには、微小に変化する数値が入る
for (let i = 0; i < nodes; i++) {
nodeX[i] = nodeStartX[i] + sin(radians(angle[i]));
nodeY[i] = nodeStartY[i] + sin(radians(angle[i]));
// frequency配列にはランダムな数値が入っているので、
// angle配列に含まれる数値も変化する。
// これがsin()に渡され、微小に変化する数値が生まれる
angle[i] += frequency[i];
}
}sin(radians(angle[i])は微小に変化する数値を生み出します。描画物が揺らいで見えるのはこのためです。
マウスに追随させ、変化に味付けをする
最後、サンプルに記述されているマウスへの追随と、ソフトボディに見える変化の味付けを加えます。下記コードの実行結果はサンプルと同じです。
const nodes = 5
const nodeStartX = [],
nodeStartY = [];
const radius = 45;
let rotAngle = -90;
let centerX, centerY;
const nodeX = [],
nodeY = [];
const angle = [],
frequency = [];
// 変化量
let accelX = 0.0,
accelY = 0.0;
// ばね効果用定数、減衰率
const springing = 0.0009,
damping = 0.98;
// ソフトボディダイナミクス
let organicConstant = 1.0;
function setup() {
createCanvas(710, 400);
centerX = width / 2;
centerY = height / 2;
init();
// 線は描画しない
noStroke();
frameRate(30);
}
function init() {
for (let i = 0; i < nodes; i++) {
nodeStartX[i] = 0;
nodeStartY[i] = 0;
nodeX[i] = 0;
nodeY[i] = 0;
angle[i] = 0;
}
for (let i = 0; i < nodes; i++) {
frequency[i] = random(5, 12);
}
}
function draw() {
// background(200);
// 前のフレームの描画結果を少し残す => にじんで見える効果が生まれる
fill(0, 100);
rect(0, 0, width, height);
drawShape();
moveShape();
}
// シェイプを描画
function drawShape() {
for (let i = 0; i < 5; i++) {
nodeStartX[i] = centerX + cos(radians(rotAngle)) * radius;
nodeStartY[i] = centerY + sin(radians(rotAngle)) * radius;
rotAngle += 360.0 / nodes;
}
drawCurveVertex();
}
// コーナーノードの値に変化を加える
function moveShape() {
// センターポイントを移動
let deltaX = mouseX - centerX;
let deltaY = mouseY - centerY;
// ばね効果を作成
deltaX *= springing;
deltaY *= springing;
accelX += deltaX;
accelY += deltaY;
// 描画物のセンターを移動
centerX += accelX;
centerY += accelY;
// ばね効果を抑制
accelX *= damping;
accelY *= damping;
// organicConstant値が小さいと、曲線の緊張度が低くなり、描画物は丸くなる
// organicConstant値が大きいと、曲線の緊張度が高まり、描画物は角張る
organicConstant = 1 - ((abs(accelX) + abs(accelY)) * 0.1);
// 参考用
text(organicConstant, 20, 20);
for (let i = 0; i < nodes; i++) {
nodeX[i] = nodeStartX[i] + sin(radians(angle[i]));
nodeY[i] = nodeStartY[i] + sin(radians(angle[i]));
angle[i] += frequency[i];
}
}
function drawCurveVertex() {
// 曲線の緊張度を変更
curveTightness(organicConstant);
fill(255);
beginShape();
for (let i = 0; i < nodes; i++) {
curveVertex(nodeX[i], nodeY[i]);
}
for (let i = 0; i < nodes - 1; i++) {
curveVertex(nodeX[i], nodeY[i]);
}
endShape(CLOSE);
}リファレンスメモ
説明
曲線の頂点座標を指定する。この関数は、beginShape()とendShape()関数の間で、beginShape()にMODEパラメータが指定されていないときだけ使用できる。WebGLモードの場合には2Dと3Dモードで使用できる。2Dモードでは2つのパラメータが、3Dモードでは3つのパラメータが必要になる。
連続するcurveVertex()線の最初と最後の点は、曲線の開始と終わりを導くために使用される。2つめと3つめの点の間に小さな曲線を描くには、最小でも4つの点が必要になる。curveVertex()で5つめの点を追加すると、2,3,4つめの点の間に曲線が描かれる。curveVertex()関数はCatmull-Romスプラインの実装。
シンタックス
curveVertex(x, y)
curveVertex(x, y, [z])
説明
curve()とcurveVertex()関数で作成される形状品質を修正する。tightness(緊張度)パラメータは、曲線が頂点にどれだけフィットするかを決める。値0.0はデフォルト値(この値はCatmull-Romスプラインになる曲線を定義する)で、値1.0はすべての点を直線で結ぶ。-5.0と5.0内の値は曲線だと認識できる程度まで変形させる。値が大きくなるとそれだけ変形の程度も大きくなる。
シンタックス
curveTightness(amount)
パラメータ
amount 数値:元の頂点から変化させる量
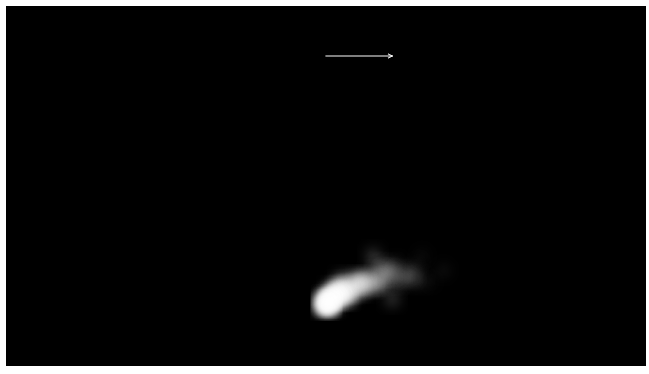
煙のパーティクル
オリジナルはダン・シフマンによるProcessing向けSmokeParticleSystemサンプル。煙のパーティクルを作成します。
sketch.js
// パーティクル用テクスチャ
let particle_texture = null;
// パーティクルシステムを保持する変数
let ps = null;
// 画像を先読み
function preload() {
particle_texture = loadImage("assets/particle_texture.png");
}
function setup() {
createCanvas(640, 360);
// パーティクルシステムを初期化。
// ParticleSystemのコンストラクタの第一引数に0を渡しているので、
// この時点ではパーティクルはまだ作成されない
ps = new ParticleSystem(0, createVector(width / 2, height - 60), particle_texture);
}
function draw() {
background(0);
// 0から640までのmouseX値を、-0.2と0.2の範囲にマッピング(対応付け)する。
let dx = map(mouseX, 0, width, -0.2, 0.2);
// dxをx成分とするベクトルを作成
let wind = createVector(dx, 0);
// システムに風のベクトル(向きと大きさ)を渡す。
// => システムはパーティクルに風のベクトルを渡す
ps.applyForce(wind);
ps.run();
// パーティクルは毎フレーム、2個作られる
for (let i = 0; i < 2; i++) {
ps.addParticle();
}
// 風力を表す矢印を描画
drawVector(wind, createVector(width / 2, 50, 0), 500);
}
/**
* "風"が吹いている方向を示す矢印を描画する
*/
function drawVector(v, loc, scale) {
push();
let arrowsize = 4;
translate(loc.x, loc.y);
stroke(255);
rotate(v.heading());
let len = v.mag() * scale;
line(0, 0, len, 0);
line(len, 0, len - arrowsize, +arrowsize / 2);
line(len, 0, len - arrowsize, -arrowsize / 2);
pop();
}ParticleSystem.js
//========= PARTICLE SYSTEM ===========
/**
* 基本的なパーティクルシステムのクラス
* @param num パーティクルの数
* @param v パーティクルシステムの位置
* @param img_ パーティクルのテクスチャ
* @constructor
*/
class ParticleSystem {
constructor(num, v, img_) {
this.particles = []; // パーティクルを管理するための配列
this.origin = v.copy(); // 誤って元データを変更した場合に備えて、ベクトル値をコピーする
this.img = img_
// num分だけ、Particleインスタンスを作成し、particles配列に追加
for (let i = 0; i < num; ++i) {
this.particles.push(new Particle(this.origin, this.img));
}
}
/**
* パーティクルシステム全体を実行
*/
run() {
// ループに使用する配列の長さを変数にメモしておく。
// forループで<variable>.lengthを目にする場合があるが、
// ループの繰り返しごとにその長さが再計算されるので、ここでは変数にメモしている。
let len = this.particles.length;
// 繰り返しパーティクルを実行、新しいものほど前面に描画
for (let i = len - 1; i >= 0; i--) {
let particle = this.particles[i];
particle.run();
// パーティクルの寿命が尽きた場合にはそれを削除する。
// javascriptの配列には'remove'がないが、"splice"でも同様に機能する。
// splice()には開始インデックスと、その位置から削除する数を与える。
if (particle.isDead()) {
this.particles.splice(i, 1);
}
}
}
/**
* 現在のすべてのパーティクルに力のベクトルを追加する
* @param dir p5.Vector、力の方向を表す
*/
applyForce(dir) {
let len = this.particles.length;
for (let i = 0; i < len; ++i) {
this.particles[i].applyForce(dir);
}
}
/**
* 新しいパーティクルをシステムに追加し、
* テクスチャを設定する
*/
addParticle() {
this.particles.push(new Particle(this.origin, this.img));
}
}Particle.js
//========= PARTICLE ===========
/**
* パーティクルをイメージで描画する、単純なParticleクラス。
*/
class Particle {
constructor(pos, img_) {
this.loc = pos.copy(); // 位置
let vx = randomGaussian() * 0.3; // x方向の速度
let vy = randomGaussian() * 0.3 - 1.0; // y方向の速度
this.vel = createVector(vx, vy); // 速度のベクトル
this.acc = createVector(); // 加速度のベクトル
this.lifespan = 100.0; // 寿命。初期値は100
this.texture = img_; // パーティクルとして使用するテクスチャ
}
/**
* パーティクルを更新して表示する
*/
run() {
this.update();
this.render();
}
/**
* パーティクルを表示する
*/
render() {
// this.loc.x, this.loc.yをイメージのセンターにして、
// this.lifespanの透明度で、this.textureを描画する
imageMode(CENTER);
tint(255, this.lifespan);
image(this.texture, this.loc.x, this.loc.y);
}
/**
* 力のベクトルをパーティクルに適用する
*/
applyForce(f) {
this.acc.add(f);
}
/**
* パーティクルがその寿命に達したかどうかを調べ、
* 達している場合にはtrueを、達していない場合にはfalseを返す
*/
isDead() {
if (this.lifespan <= 0.0) {
return true;
}
else {
return false;
}
}
/**
* パーティクルの位置を更新する
*/
update() {
this.vel.add(this.acc); // 加速度は速度を変更する
this.loc.add(this.vel); // 速度は位置を変更する
this.lifespan -= 2.5; // 更新のたびに寿命が短くなる
this.acc.mult(0); // 毎回、加速度を0にリセットする
}
}下の実行画面写真のクリックでサンプルが開きます。
解説
前に見たパーティクルサンプルと、コード自体に大きな違いはありませんが、いくつかの特徴や覚えておきたいテクニックなどを以下で見ていきます。
パーティクルのイメージ
このサンプルの特徴は、パーティクルの表現に画像のイメージを使用している点です。画像を使用することで、表現の幅が大きく広がります。
使用されている画像は下図のparticle_texture.pngファイルです。サイズは32 x 32で、アルファチャンネルのみ持っています。
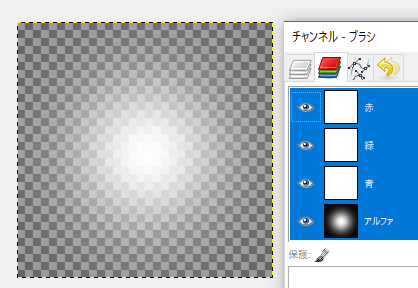
この画像はイメージとして、ParticleSystemクラスを経由して、Particleクラスにthis.textureとして渡されます。Particleクラスのrender()メソッドでは、次のように使用されます。
render() {
imageMode(CENTER);
tint(255, this.lifespan);
image(this.texture, this.loc.x, this.loc.y);
}imageMode(CENTER)は、image()関数が使用されるとき、その2つめと3つめのパラメータをイメージの中心点と解釈します。したがってthis.loc.x, this.loc.yがセンターとなります(参考:「5_3:移動(translate)と回転(rotate) p5.js JavaScript」)。
tint(255, this.lifespan)は、重ね塗りの色を白にすることで、イメージのカラーに影響させずに、透明度だけをthis.lifespanに変更するテクニックです。this.lifespanはパーティクルの寿命に応じて小さくなっていくので、パーティクル自体はどんどん透明に近づいていきます(参考:「6:イメージ(Image)」)。
map()関数のうまい使用法
テクニックとして優れているのが、map()関数の使い方です。それはsketch.jsのdraw()内にあります。
let dx = map(mouseX, 0, width, -0.2, 0.2);
let wind = createVector(dx, 0);
ps.applyForce(wind);map(mouseX, 0, width, -0.2, 0.2)によって、0から640までのmouseX値が、-0.2と0.2までの範囲にマッピング(対応付け)されます。これは、map()が返すdxが、マウスがキャンバスセンターにあるときは0、それより左にあるときは負、右にあるときは正になる、ということです。このサンプルでは、マウスの位置に応じて風の向きを変えたいので、このdx値がうまい具合にベクトルとして使用できます。
ベクトルの矢印の描画
sketch.jsのdrawVector()関数は、受け取ったベクトルの向きと大きさをキャンバスに描画します。この関数で使われているテクニックは、覚えておいて損はありません。以下は簡単な例です。
// drawVectorサンプル
let centerPoint;
const scale = 100;
const arrowsize = 10;
function setup() {
createCanvas(400, 300);
centerPoint = createVector(width / 2, height / 2);
}
function draw() {
background(200);
// 0から640までのmouseX値を、-1と1の範囲にマッピング(対応付け)する。
let dx = map(mouseX, 0, width, -1, 1);
// dxをx成分とするベクトルを作成
let vec = createVector(dx, 0);
// 参考用に左上に描画
text(vec, 10, 20);
drawVector(vec);
}
function drawVector(v) {
// 参考用に左上に描画
text(v.heading(), 10, 50);
push();
// 座標システムをcenterPointに移動
translate(centerPoint.x, centerPoint.y);
stroke('red');
// vの向いている方向に回転(右か左)
rotate(v.heading());
// vの大きさを、見やすくするため適当に拡大
let len = v.mag() * scale;
// 線と矢印の線を描画
line(0, 0, len, 0);
line(len, 0, len - arrowsize, +arrowsize / 2);
line(len, 0, len - arrowsize, -arrowsize / 2);
pop();
}ブラウン運動
ランダムな運動を、連続する線で記録します。オリジナルはProcessingの同サンプル。
const num = 2000;
const range = 6;
const ax = [];
const ay = [];
function setup() {
createCanvas(710, 400);
for (let i = 0; i < num; i++) {
ax[i] = width / 2;
ay[i] = height / 2;
}
frameRate(30);
}
function draw() {
background(0);
// => 末尾の値のみ変わらず、ほかは1つ左に移動する
for (let i = 1; i < num; i++) {
ax[i - 1] = ax[i];
ay[i - 1] = ay[i];
}
// 末尾の値に、-6から6の間のランダムな浮動小数点数を加算
// => 新しい値になる。これが運動の変化をもたらす元
ax[num - 1] += random(-range, range);
ay[num - 1] += random(-range, range);
// 加算した末尾の値を、キャンバスの幅と高さに制限
ax[num - 1] = constrain(ax[num - 1], 0, width);
ay[num - 1] = constrain(ay[num - 1], 0, height);
// 点を結んで線を描く
for (let j = 1; j < num; j++) {
// valは51以上255未満の数値
const val = j / num * 204.0 + 51;
stroke(val);
line(ax[j - 1], ay[j - 1], ax[j], ay[j]);
}
}解説
「ブラウン運動」とは、気体や液体に含まれる微粒子がちょこまか動く運動のことを言います。
「動き回る分子-ブラウン運動-」より引用
【ブラウン運動とは】
気体や液体の分子は、たえず熱運動をしています。そして気体中や液体中にある微粒子も、これらいくつかの分子に衝突され続けています。その結果、微粒子は不規則に動かされることになります。このような微粒子の運動を「ブラウン運動」といいます。
微粒子を浮かべる気体や液体の種類によらず、ブラウン運動はおこります。ブラウン運動は、温度が高いほど、微粒子が小さいほど激しくなります。
【ブラウン運動の発見】
1827年、イギリスの植物学者ロバート・ブラウンは、花粉を水のなかに入れて顕微鏡で観察していたところ、花粉からでた微粒子がたえず細かく不規則に動いていることに気づきました。最初は生物だから自分で動いているのだろうとブラウンは考えました。しかし、いろいろ調べてみて石の粉のように生命のないものでも、同じように動くことを発見しました。
ブラウンはこの運動の原因を解明することはできませんでしたが、発見者の名前にちなんで「ブラウン運動」とよばれています。
これをシミュレーションしようというのがこのサンプルです。ブラウン運動の動きは、何の意思もなく、何の力も作用せずに勝手に動いているように見せたいときに利用できるテクニックです。
配列の巧みな操作
上記サンプルは実は、2000個の数値の要素を持つ配列を巧みに操作して、1回のdraw()関数の呼び出しで、最高2000本の線を描いています。コード自体は短く、複雑ではないのですが、非常に洗練されています。
以下では要素数を4個にし(num = 4)、配列axだけに注目してその操作内容を具体的に見ていきます。
まず最初に次のforループがあります。
for (let i = 0; i < num; i++) {
ax[i] = width / 2;
ay[i] = height / 2;
}numは4でwidthは710なので、配列axは [355, 355, 355, 355] となります。これが初期値です。
つづいて、次のforループがあります。これは[i – 1]番めの要素をi番めの要素にする、つまり、配列の最後の要素だけ変わらず、ほかは左に1つシフトする、ということです。iは1から始まっているので、ループの初回はax[0] = ax[1]となり、1番めの要素が0番めの要素に置き換わります。しかしaxは [355, 355, 355, 355]のままです。
for (let i = 1; i < num; i++) {
ax[i - 1] = ax[i];
ay[i - 1] = ay[i];
}次はこのコードです。[num -1]は、上のループでそのままにしておいた配列の最後の要素です。これに、random(-range, range)、つまり-6から6の間のランダムな浮動小数点数が加算されます。axはたとえば、[355, 355, 355, 350.59480348791004]になります。
ax[num - 1] += random(-range, range);
ay[num - 1] += random(-range, range);その後、加算した末尾の値をキャンバスの幅内に納めます。これは理解しやすい処理で、線がキャンバスの外に描かれないようにするためです。
ax[num - 1] = constrain(ax[num - 1], 0, width);
ay[num - 1] = constrain(ay[num - 1], 0, height);そして最後、次のforループで線が描かれます。変数valについては後述します。
for (let j = 1; j < num; j++) {
const val = j / num * 204.0 + 51;
stroke(val);
line(ax[j - 1], ay[j - 1], ax[j], ay[j]);
}今、axは[355, 355, 355, 350.59480348791004]です。jは1から始まるので、j=1のときにはax[0]とax[1]の間に線が引かれます。しかし両方とも355なので、線は実際には描かれません。実際に線になるのは、 355と 350.59480348791004の間です。以上が1回めのdraw()関数の実行内容です。

2回めには、同様の処理により、[355, 355, 355, 350.59480348791004]は、たとえば[355, 355, 350.59480348791004, 350.5933130199435]になります。1回めで最後の要素であった350.5948…はaxの2番めの要素になり、最後には新しい350.593…が入っています。ここでも355と355の間に線は引かれませんが、1回めで引いた355と350.594…の間と、350.594…と新しい350.593…の間に線は描かれます。つまり線は2本、前回と同じものと新しいものの2本が描かれます。
3回めも同様に進み、たとえば[355, 350.59480348791004, 350.5933130199435, 348.26374454420915]になります。355と350.594…と350.593…が左に1つシフトし、新しい348.263が加わっています。これらの数値を元に今度は、前と同じ線が2本、新しい線が1本の合計3本の線が描かれます。
そして4回め、つまりnum回め、axから355はなくなり、たとえば[350.59480348791004, 350.5933130199435, 348.26374454420915, 350.52733912439714]になります。355と350.594…を結ぶ線がなくなり、新たに348.263と350.527を結ぶ線が加わって3本の線が引かれます。これは、num回めからは一番古い線が描かれなくなるということを意味しています。
線の色の巧みな設定
描く線の色は、最後のforループのval変数の値で決まります。
for (let j = 1; j < num; j++) {
const val = j / num * 204.0 + 51;
stroke(val);
line(ax[j - 1], ay[j - 1], ax[j], ay[j]);
}val値を計算する j / num * 204.0 + 51 は、一体何をやっているのでしょう?
numがサンプルで使われている2000だとすると、j / num * 204.0 は、j=1のとき1/2000*204で、j=2のとき2/2000*204、j=3のとき3/2000*204 です。これは下図のように考えることができます。
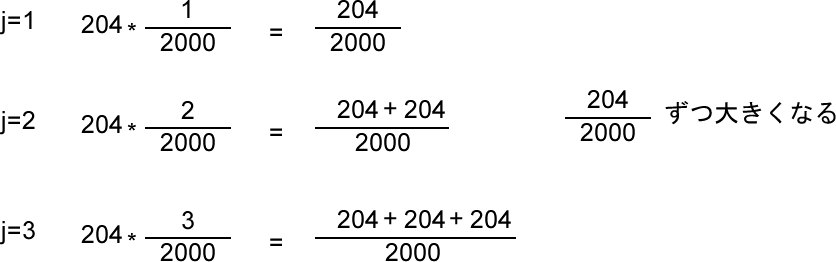
jが1大きくなるごとに、j / num * 204.0 は、204/2000ずつ大きくなります。204/2000は204の2000等分なので、言い換えると、jが1大きくなるごとに、204の2000等分を足しているということです。jはnum未満まで1ずつ大きくなるので、ループの最後jは1999で、1999/2000*204.0(=203.898)は204に非常に近くなります。したがって、j / num * 204.0は、204/2000(=0.102)を最小値、204未満を最大値として、204の2000等分をj分だけ足した数値を生み出す、と言えます。
一方、204は255の80%に当たる数値で、51は255から204を引いた数値なので、j / num * 204.0 + 51 は、255の0%から80%まで変化する数値に、残りの20%を足す、と見なすことができます。

ループの最初のj=1のとき、valは204の0% + 51なので、stroke()は線を51のグレーに設定します。51のグレーはRGB(51,51,51)なので、上図でも分かるように、かなり暗い色です。ループの最後、j=1999のときにはvalは255に非常に近い数値になるで、線の色は白になります。ここから分かるのは、ループが進むにつれ、線の色は暗いグレーから白に近づく、ということです。
配列axの要素の数値は、draw()関数が呼び出されるたびに、左に1つずつシフトするので、同じ位置に描かれる線の色は次第に濃くなります。これは、前に描かれた線の色は時間とともにだんだん濃くなっていくように見える、という効果を生み出します。
前にnum回めからは一番古い線が描かれなくなると述べましたが、この線の座標は、最後に描かれるときはaxの一番左(0番めの要素)にあります。この線の色は51の濃いグレーです。背景の黒(background(9))とほとんど見分けがつかないので、次のフレームでこの線が描かれないと、自然に消えてなくなった、ように見えます。
ばねのチェーン
上の重りはゴム状のひもでマウス位置につながれ、下の重りは上の重りにゴム状のひもでつながれています。重力は両方の重りに作用します。Processingサンプルからの移植。
sketch.js
const gravity = 9.0; // 重力
const mass = 2.0; // 質量
let s1, s2; // Spring2Dオブジェクト
function setup() {
createCanvas(720, 400);
fill(255, 126);
// xとy位置、質量、重力を渡してSpring2Dオブジェクトを2つ作成する
s1 = new Spring2D(0.0, width / 2, mass, gravity);
s2 = new Spring2D(0.0, width / 2, mass, gravity);
}
function draw() {
background(0);
// 接続先を指定して、更新と表示
s1.update(mouseX, mouseY);
s1.display(mouseX, mouseY);
s2.update(s1.x, s1.y);
s2.display(s1.x, s1.y);
}Spring2D.js
// Spring2Dクラス
// ゴム状のひもの上は接続先にぶら下がり、下には重りがついている
class Spring2D {
constructor(xpos, ypos, m, g) {
this.x = xpos; // x位置
this.y = ypos; // y位置
this.vx = 0; // x方向の速度
this.vy = 0; // y方向の速度
this.mass = m; // 質量
this.gravity = g; // 重力
this.radius = 30; // 半径
// 剛性 => かかる力に対する変化のしづらさの度合い
this.stiffness = 0.2;
this.damping = 0.7; // 減衰率
}
// 位置を更新する
update(targetX, targetY) {
// 重り接続先の真下に移動しようとするので、その差が力になる
// そのときにはひもの剛性が関係する(大きいほど力が大きくなる)
let forceX = (targetX - this.x) * this.stiffness;
// 加速度:f=ma => a=f/m 加速度は力/質量
let ax = forceX / this.mass;
// 速度:(今の速度+加速度)に減衰率を掛ける
this.vx = this.damping * (this.vx + ax);
// 新しい位置:新しい速度に現在位置を足す
this.x += this.vx;
let forceY = (targetY - this.y) * this.stiffness;
// y方向の場合はさらに重力を加える
forceY += this.gravity;
let ay = forceY / this.mass;
this.vy = this.damping * (this.vy + ay);
this.y += this.vy;
}
// 表示する
display(nx, ny) {
noStroke();
// 円を描画
ellipse(this.x, this.y, this.radius * 2, this.radius * 2);
stroke(255);
// ぶら下がり先(nx, ny)まで線をひく
// this.xとthis.yの計算には、剛性が関係しているので、この線は伸びたり縮んだりする
line(this.x, this.y, nx, ny);
}
}解説
これは、ゴム状のひもでつないだ2つの重りのシミュレーションです。ゴム状のひもの伸び縮みはばねと考えることができます。ただし、上の重りのひもの先はマウス位置に、下の重りのひもの先は上の重りにつなぐ必要があるので、シミュレーションの実現はかなり難しそうに思えます。
Spring2Dクラスのstiffnessプロパティは、剛性と呼ばれるものの概念を表します。
this.stiffness = 0.2;剛性は”かかる力に対する変化のしづらさの度合い”で、大きいほどひもがより硬く短くなり、小さいほどより柔らかく長くなります。
剛性:剛性(ごうせい、英: stiffness)とは、曲げやねじりの力に対する、寸法変化(変形)のしづらさの度合いのこと。力に対して変形が小さい時は剛性が高い(大きい)、変形が大きい時は剛性が低い(小さい)という。工学的には単位変形を起こすのに必要な力(荷重/変形量)で表され、フックの法則におけるばね定数も剛性の一種である。剛性とは逆の変形のしやすさの度合い(変形量/荷重)は柔性(じゅうせい)と呼ばれる(ウィキペディアの「剛性」より)。
Spring2Dインスタンスのupdate()メソッドは、sketch.jsのdraw()関数から毎フレーム、接続先(ぶら下がり先)の位置を渡されて呼び出されます。重りが上の重りだろうが下の重りだろうかは関係ありません。Spring2Dインスタンスは自分がチェーンのどこに位置するのかを知る必要はなく、ただぶら下がり先の位置を受け取るだけです。
ひもの接続先からずれた位置にある重りには、そこから安定した静止位置(接続先の真下)に戻ろうとする力が働くと考えられます。これを表すのがupdate()メソッドの変数forceXとforceYです。しかし、一瞬で戻るのではなく、そこには剛性要因が想定できます。これは今の場合、ひもの張り具合、ゴムの強さ、といったものです。これを表す値(this.stiffness)を掛けます。後は前と同様の加速度と速度、現在位置の計算です。
ただし、重りには鉛直方向の力が加わるので、forceYにはそれに相当するthis.gravityを加えます。
let forceY = (targetY - this.y) * this.stiffness;
// y方向の場合はさらに重力を加える
forceY += this.gravity;
let ay = forceY / this.mass;
this.vy = this.damping * (this.vy + ay);
this.y += this.vy;以上で、ひもでつないだ2つの重りのシミュレーションは実現できます。一見非常に難しそうに思えるシミュレーションですが、Spring2Dインスタンスに接続先を教え、剛性と重力を加えた、さほど難しくない毎フレームの更新で実現できています。不思議な気がしますが、ためしにSpring2Dインスタンスをもう1つ作成し、update()とdraw()メソッドでs2を指定してやるだけで、チェーンを増やすことができます。
実際はイージングと重力加算
このサンプルは、物理法則を適用したシミュレーションなので、力や質量、剛性といった概念やニュートンの第二法則にともなう計算が出てきますが、実際に求められる計算結果は、「4_3:応答:イージングの導入 p5.js JavaScript」で述べているイージングと一部をのぞいて変わりません。
// 残りの距離
const dx = targetXpos - xpos;
// 速度は残りの距離に、距離の何分の1かを掛けたもの
const vx = dx * easing;
// 新しい現在位置は、前の現在位置に速度を足したもの
xpos = xpos + vx;
ellipse(xpos, 60, 10, 10);一部というのは、forceY += this.gravityの計算です。ためしにupdate()メソッドからこの行をのぞいて実行すると、円がマウス位置に近づくイージングのアニメーションになります。
(スノーフレーク)
落下する雪(スノーフレーク)の運動をシミュレーションするパーティクルシステム。オブジェクトの配列を使って、スノーフレークのパーティクルを保持します。Aatish Bhatiaによる寄稿。
sketch.js
const snowflakes = []; // Snowflakeオブジェクトを保持する配列
function setup() {
createCanvas(400, 600);
fill(240);
noStroke();
}
function draw() {
background('brown');
const t = frameCount / 60; // 更新時間
// 毎フレーム、ランダムな数の雪を作成する
for (let i = 0; i < random(5); i++) {
// Snowflakeインスタンスを作成し、snowflakes配列に追加
snowflakes.push(new Snowflake());
}
// for..ofループでsnowflakes配列を走査
for (const flake of snowflakes) {
flake.update(t); // 雪の位置を更新
flake.display(); // 雪を描画
}
}Snowflake.js
// Snowflakeクラス
class Snowflake {
constructor() {
// 座標を初期化
this.posX = 0;
// posYはキャンバス上端より上
this.posY = random(-50, 0);
// 最初の角度
this.initialangle = random(0, TWO_PI);
// ランダムなサイズ
this.size = random(2, 5);
// 雪が沿って落下するらせんの半径
// 領域に均一に広がるように設定
// radiusは幅の半分未満を最高値とするランダムな値
this.radius = sqrt(random(pow(width / 2, 2)));
}
update(time) {
// x位置は円に沿う
let w = 0.6; // 角速度
// timeは毎回大きくなるので、angleも大きくなる
let angle = w * time + this.initialangle;
// 滑らかに変化するサイン波の値を得る
this.posX = width / 2 + this.radius * sin(angle);
// サイズによって、y速度を少し変えて落下するようにする
this.posY += pow(this.size, 0.5);
// キャンバスの下端から出たら消去
if (this.posY > height) {
// 注意:このsnowflakesはsketch.jsの配列snowflakesで、
// すべてのSnowflakeインスタンスで共通して使用している
let index = snowflakes.indexOf(this);
snowflakes.splice(index, 1);
}
}
display() {
ellipse(this.posX, this.posY, this.size);
}
}下の実行画面写真のクリックでサンプルが開きます。
解説
これは定番とも言える雪降らしのサンプルで、「JavaScript snowflake」や「JavaScript snowfall」といったワードで検索すると、多くの作例を見ることができます。
多くの雪を連続して作成し落下させる方法は、前に見たパーティクルのテクニックによるものですが、このサンプルを実行してよく観察すると、
- 雪は画面上端の幅全体から落ちて来る => 一カ所から噴き出しているのではない
- 雪は舞っているように見える => まっすぐ落ちているのではない
- 雪は大きいものや小さいものがあり、大きいものの方が速く落ちるように見える
といったことに気づきます。これらはどれも、”雪が降っているように見せる”ためのテクニックなのです。雪のひとひら(snowflake)1つ1つはパーティクルで、Snowflakeクラスのインスタンスです。これをsketch.jsからたくさん作成して、それぞれの更新と表示のメソッドを呼び出します。1つ1つの雪は自身のposXとposYプロパティを使って、落ちていく雪のように振る舞います。
雪のふるまいは位置決めの方法で決まります。雪の位置を決めるのはposXとposYなので、この2つの変数を中心に見ていきましょう。
posXの変化を探る
Snowflakeクラスのコンストラクタ関数内に次のコードがあります。これはSnowflakeインスタンスのradius(半径の意)プロパティの値を初期化するコードですが、直感的には何をしようとしているのか分かりません。
// 雪が沿って落下するらせんの半径
// 領域に均一に広がるように設定
// radiusは幅の半分未満を最高値とするランダムな値
this.radius = sqrt(random(pow(width / 2, 2)));sqrt(random(pow(width / 2, 2)))を言葉にすると、0とキャンバスの幅の2乗の範囲からランダムな浮動小数点数を得て、その数値の平方根をradiusの値に設定する、です。radius値は一定でなくインスタンスごとに変化する値であり、その後、Snowflakeインスタンスのx位置(posXプロパティ)の設定に使われているので、これを探ってみましょう。
次のコードは、Snowflake.jsからradiusとposXの設定に必要だと思われるコードを抜き出したものです。
let initialangle;
let radius;
const w = 0.6; // 角速度
function setup() {
canvas = createCanvas(400, 600);
fill(240);
// 最初の角度をランダムに決める
initialangle = random(0, TWO_PI);
print('最初の角度: ' + initialangle)
// 雪が沿って落下するらせんの半径
// 領域に均一に広がるように設定
// 幅の半分未満を最高値とするランダムな値を得る
// => 0より大きく幅の半分(200)未満のランダムな浮動小数点数
radius = sqrt(random(pow(width / 2, 2)));
print('半径:' + radius);
}
function draw() {
background(200);
// frameCountを使って一定の割合で大きくなる数値を作成
const t = frameCount / 60;
// tをupdate()関数に渡して呼び出す
update(t);
// 適当な時間が経過したら停める
}
function update(time) {
// radiusをwidth / 2, 0)を中心とする円の半径として描画
// radiusは0から幅の半分までのランダムな値なので、円はキャンバス内に収まる
ellipse(width / 2, 0, radius * 2);
// radiusの長さを円の半径として太い赤線で描画
strokeWeight(4);
stroke(255, 0, 0);
line(width / 2, 0, width / 2 + radius, 0);
strokeWeight(1);
stroke(0);
// time値は一定の割合で大きくなるので、angleも大きくなる
let angle = w * time + initialangle;
// posXは半円の左端(width/2-radius)を最小値に、半円の右端(width/2+radius)を最大値として
// 滑らかに変化しつづける数値
let posX = radius * sin(angle) + width / 2;
ellipse(posX, 0, 10, 10);
}radiusは実行するたびに変化するので、それを半径とする円の大きさも変わります。また半円の直径上を小さな円が左右に移動します。これはposXの変化の様子を示しています。
上記コードを解説します。
setup()関数の initialangle = random(0, TWO_PI) によって0度以上360度未満の度数(ラジアン値)が変数initialangleに代入されます。これはupdate()関数でsin()に渡す角度の一部として使用されます。initialangleは実行するたびに値が変わるので、sin()に渡される値も同様に変わることになります。radius = sqrt(random(pow(width / 2, 2))) によって、0以上キャンバスの幅未満の浮動小数点数が変数radiusに代入されます。この値は後で円の描画とposXの設定に使用します。
draw()関数では、まず const t = frameCount / 60 で変数tの値を決めています。frameCountはp5.jsのシステム変数で、スタート時からの描画回数(draw()が呼び出された回数)を保持します。これを毎フレーム、p5.jsの標準フレームレートである60で割っているので、tは秒数ということになります。tは確実に大きくなる数値です。
update()関数では、setup()関数で値を入れたradiusを使って、点(width / 2, 0)を中心とする半径radiusの円を描いています。キャンバス上端の真ん中が円の中心なので、描かれる円は半円になります。radiusはこのコードを実行するたびに値が変わるので、描画する円の大きさも変わります。その後は、半円の中心からx軸方向に長さがradiusの太い赤線を引いています。半径がradiusである円をこのように描くと、前の sqrt(random(pow(width / 2, 2))) という計算は、このキャンバスの幅に必ず収まる円の半径の長さを得る方法のように思えます。
つづいてposXの計算です。update()関数には経過秒数が渡され、それに0.6が代入された変数wを掛け、その結果にラジアン単位のinitialangleを足しているので、変数angleは時間経過とともに必ず大きくなる値になります。posXの計算ではこれを次のように使用しています。
let posX = radius * sin(angle) + width / 2;これは、「7_6:円運動 p5.js JavaScript」の円周上の点を求める式と同じです。ここでは実際に円の直径上を移動する小さな円を描画しています。
小さな円の移動から分かるように、posXは(width/2-radius)を最小値に、(width/2+radius)を最大値として滑らかに変化しつづける数値です。以上をまとめると、radius = sqrt(random(pow(width / 2, 2)))によって、0より大きく幅の半分未満のランダムな数値がradiusに代入され、その後radiusとsin()関数、変数angleを使って、(width/2-radius)を最小値、(width/2+radius)を最大値として滑らかに変化する数値をposXに代入しています。
リファレンスメモ
説明
数値の平方根を計算する。数値の平方根は、有効な負の根であっても、つねに正。数値の平方根はs*s = aのようなもので、2乗の逆。Math.sqrt()をマッピングしたもの。
シンタックス
sqrt(n)
パラメータ
n 数値:負でない数値
戻り値
数値:数値の平方根
説明
指数表現を容易にする。pow()関数は、数値そのもの(やその逆数)を大量に乗算するときの有効な方法。たとえばpow(3, 5)は式 3 × 3 × 3 × 3 × 3 と同じで、pow(3, -5)は式1 / 3 × 3 × 3 × 3 × 3 と同じ。Math.pow()をマッピングしたもの
シンタックス
pow(n, e)
パラメータ
n 数値:指数表現の底
e 数値:底を累乗する指数
戻り値
数値: n^e (nのe乗)
posYの変化を探る
posXの変化の様子が分かったので、次はposYです。posYは次の1行で決まります。
posY += pow(size / 2, 0.5);一見やさしそうに見えますが、実は、なぜpow()関数を用いているのか、sizeの半分の0.5乗とは何なのか、よく分かりません。これを次のコードで見ていきましょう。
let initialangle;
let radius;
const w = 0.6;
// 新たに加えた変数
let posY, size;
function setup() {
createCanvas(400, 600);
noFill();
initialangle = random(0, TWO_PI);
radius = sqrt(random(pow(width / 2, 2)));
print('radius; ' + radius)
// 初期化
posY = 0;
size = random(2, 5);
background(200);
print('size; ' + size)
print('pow(size, 0.5); ' + pow(size, 0.5))
print('sqrt(size); ' + sqrt(size))
}
function draw() {
const t = frameCount / 60;
update(t);
// 適当な時間が経過したら停める
if (frameCount > 650) {
noLoop();
}
}
function update(time) {
// posXの変化が収まる幅の矩形を描画
rect(width / 2 - radius, 0, radius * 2, height);
let angle = w * time + initialangle;
let posX = radius * sin(angle) + width / 2;
// 2乗するとsizeになる数値をposYに足す
// sizeの大きい物ほど速く落下する => 近いものほど速く落下するように見える3D効果がある
posY += pow(size / 2, 0.5);
// 円を描画 => 軌跡はらせん状になる
ellipse(posX, posY, size);
}このコードを実行すると、下図のような結果になります。垂直方向の2本の線は、半径がradiusの円の直径です。radiusは実行するたびに値が変わるので、この2本の線の幅(実際には矩形の幅)も変わります。そして背景をクリアせずに(background()を使わず)posXとposYの位置に円を描いているので、円の軌跡が描画されます。この線は雪が沿って落ちていく曲線です。
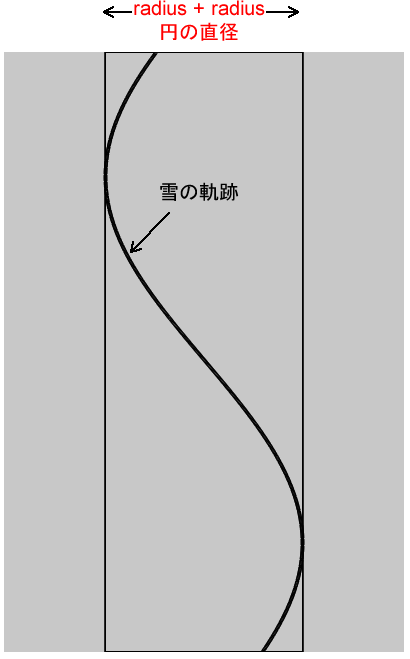
変数posYは最初0で、sizeは2以上5未満の浮動小数点数です。pow(size, 0.5)、つまりsizeの0.5乗は、2乗するとsizeになる数値です。これはsqrt(size)、つまりsizeの平方根です。
posYは最初0で、その後draw()関数から呼び出されるupdate()関数で pow(size / 2, 0.5)分だけ加算されます。これはsizeの平方根です。このサンプルの作者はなぜsizeの平方根を毎フレーム、足しているのか、方々調べた結果、「終端速度は水滴の半径の平方根に比例する」という記述が見つかりました(「第4章 雨滴の落下速度」)。
物理学的な詳細はさておき、ここでのポイントは、size値が大きい方が速く落下するということです。雪のひとひらは大きい方が空気抵抗が大きくなって、ゆっくり落下するように見えるので、大きい雪は近くの雪、小さい雪は遠くの雪、と考えると、size値の大きい方が速く落下するこの仕様は3D効果を狙っていると言えるかもしれません。
ペンローズ・タイル
David Blitzによる、processing.org/examplesからの”ペンローズ・タイル”サンプルの移植
sketch.js
let ds;
function setup() {
createCanvas(710, 400);
ds = new PenroseLSystem();
// 次のコードの数値を変えて試してみて
ds.simulate(5);
}
function draw() {
background(0);
ds.render();
}PenroseLSystem.js
// PenroseLSystemクラス
class PenroseLSystem {
constructor() {
this.steps = 0;
// ペンローズひし形L-system用の初期値(axiom)とルール
// 参照先はよくできているが、わたしはよいものが見つけられなかった
this.axiom = "[X]++[X]++[X]++[X]++[X]";
this.ruleW = "YF++ZF----XF[-YF----WF]++";
this.ruleX = "+YF--ZF[---WF--XF]+";
this.ruleY = "-WF++XF[+++YF++ZF]-";
this.ruleZ = "--YF++++WF[+ZF++++XF]--XF";
// 次の値を変えて試してみて
this.startLength = 460.0;
this.theta = TWO_PI / 10.0; //30度。TWO_PI / 6.0なども試してみて
this.reset();
}
simulate(gen) {
// 世代(this.generations)がgen未満である間
while (this.getAge() < gen) {
// iterate()メソッドにproductionプロパティを渡して実行しつづける
// プロダクション => システムをある文字列から次の文字列に進化させるルール
this.iterate(this.production);
}
}
reset() {
this.production = this.axiom;
this.drawLength = this.startLength;
this.generations = 0;
}
getAge() {
return this.generations;
}
// 置換ルールを適用して、プロダクション文字列の新しい繰り返しを作成する
iterate() {
let newProduction = "";
for (let i = 0; i < this.production.length; ++i) {
let step = this.production.charAt(i);
// 対象の文字(step)が'W'なら、ルールruleWで置換する
if (step === 'W') {
newProduction = newProduction + this.ruleW;
}
// そうでなく'X'なら、ルールruleXで置換する
else if (step === 'X') {
newProduction = newProduction + this.ruleX;
}
// そうでなく'Y'なら、ルールruleYで置換する
else if (step === 'Y') {
newProduction = newProduction + this.ruleY;
}
// そうでなく'Z'なら、ルールruleZで置換する
else if (step === 'Z') {
newProduction = newProduction + this.ruleZ;
}
// 以上のどれにも当てはまらない場合
else {
// 'F'文字はとばし、そのほかの文字('+', '-', '[', ']')には触れない
if (step != 'F') {
newProduction = newProduction + step;
}
}
}
// drawLengthを半分に
this.drawLength = this.drawLength * 0.5;
// generationsをインクリメント
this.generations++;
// productionを今作成したnewProductionに
this.production = newProduction;
}
// プロダクション文字列をタートルグラフィックに変換
render() {
// 座標システムをキャンバスセンターに移動
translate(width / 2, height / 2);
this.steps += 20;
if (this.steps > this.production.length) {
this.steps = this.production.length;
}
for (let i = 0; i < this.steps; ++i) {
let step = this.production.charAt(i);
// 'W', 'X', 'Y', 'Z'は実際にはタートルアクションには対応しない
// 対象の文字(step)が'F'なら
if (step === 'F') {
stroke(255, 60);
// repeats回だけ
for (let j = 0; j < this.repeats; j++) {
// 真上に長さdrawLengthの線を引く
line(0, 0, 0, -this.drawLength);
noFill();
// drawLength分、上に座標システムを移す
translate(0, -this.drawLength);
}
// repeatsを1に
this.repeats = 1;
}
// そうでなく'+'なら
else if (step == '+') {
// theta度だけ回転
rotate(this.theta);
}
// そうでなく'-'なら
else if (step == '-') {
// -theta度だけ回転
rotate(-this.theta);
}
// そうでなく'['なら
else if (step == '[') {
// 変換を開始
push();
}
// そうでなく']'なら
else if (step == ']') {
// 変換を終了
pop();
}
}
}
}下の実行画面写真のクリックでサンプルが開きます。
解説
ペンローズ・タイルは、1966年、イギリスの物理学者ロジャー・ペンローズが考案した、2種類のひし形を使って平面を隙間なく埋める手法で、並び方に一定の規則性があるものの周期性がなく、局所的に5回対称性を持つことが特徴とされます。5回対称性とは、「中心となる点を持つ図形、例えば正五角形を重心周りに360°/5 = 72°回転しても図形が重なることをいいます」(「自然の美しさと対称性」)。
下図はペンローズ・タイルのパターンとそこに含まれる5回対称性を示しています(「『準結晶』の発見 2011年ノーベル化学賞解説」)。
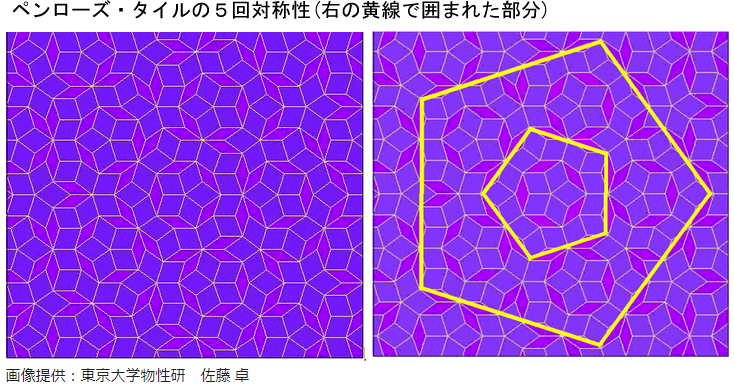
このサンプルは、このペンローズ・タイルを、L-systemによって描画するものです。L-systemについては、前の「9:シミュレーション 1/2 (Simulate)」で詳しく見ています。
上記サンプルコードはいささか長く結果を一度に描画しないので、短く書き直してみました。
// ルールとルールにもとづく初期値
const axiom = "[X]++[X]++[X]++[X]++[X]";
const ruleW = "YF++ZF----XF[-YF----WF]++";
const ruleX = "+YF--ZF[---WF--XF]+";
const ruleY = "-WF++XF[+++YF++ZF]-";
const ruleZ = "--YF++++WF[+ZF++++XF]--XF";
// プロダクション文字列(ルールの適用によって生成される文字列)
let production;
// 線の長さ
let drawLength = 300;
// 角度
let theta;
// 次世代の文字列の作成回数を追跡する
let generations = 0;
// 次世代の文字列を作成する回数
const gen = 1;
function setup() {
createCanvas(600, 600);
theta = TWO_PI / 10.0;
production = axiom;
}
function draw() {
background(151, 219, 233);
// 次世代を作成する回数未満に達するまで
while (generations < gen) {
// 繰り返し次世代文字列を作成する
iterate();
}
// 次世代文字列の作成が終わったら、文字列を線で描画
render();
}
// 次世代文字列を作成する
function iterate() {
let newProduction = "";
for (let i = 0; i < production.length; ++i) {
// プロダクション文字列に含まれる対象文字
let step = production.charAt(i);
// 対象文字が'W'なら、ルールruleWを適用
if (step === 'W') {
newProduction = newProduction + ruleW;
}
// そうでなく'X'なら、ルールruleXを適用
else if (step === 'X') {
newProduction = newProduction + ruleX;
}
// そうでなく'Y'なら、ルールruleYを適用
else if (step === 'Y') {
newProduction = newProduction + ruleY;
}
// そうでなく'Z'なら、ルールruleZを適用
else if (step === 'Z') {
newProduction = newProduction + ruleZ;
}
// 以上のどれにも当てはまらない場合
else {
// 'F'文字はとばし、そのほかの文字('+', '-', '[', ']')には触れない
if (step != 'F') {
newProduction = newProduction + step;
}
}
}
// drawLengthを半分に
drawLength = drawLength * 0.5;
// generationsをインクリメント
generations++;
// productionを今作成したnewProductionに
production = newProduction;
// print(production);
}
function render() {
// 座標システムをキャンバスセンターに移動
translate(width / 2, height / 2);
let len = production.length;
for (let i = 0; i < len; ++i) {
// 'W', 'X', 'Y', 'Z'文字は実際には描画に関係しない
// プロダクション文字列に含まれる対象文字
let step = production.charAt(i);
// 対象の文字が'F'なら
if (step === 'F') {
stroke(81, 61, 230);
// 真上に長さdrawLengthの線を引く
line(0, 0, 0, -drawLength);
// 引いた線の始点に座標システムを移す
translate(0, -drawLength);
}
// そうでなく'+'なら
else if (step == '+') {
// theta度だけ回転
rotate(theta);
}
// そうでなく'-'なら
else if (step == '-') {
// -theta度だけ回転
rotate(-theta);
}
// そうでなく'['なら
else if (step == '[') {
// 変換を開始
push();
}
// そうでなく']'なら
else if (step == ']') {
// 変換を終了
pop();
}
}
}このコードでは、変数genで次世代の文字列を作成する回数が指定できます。上記では gen=1 なので、1つ後の世代が作成され描画されます。下図はその結果です。
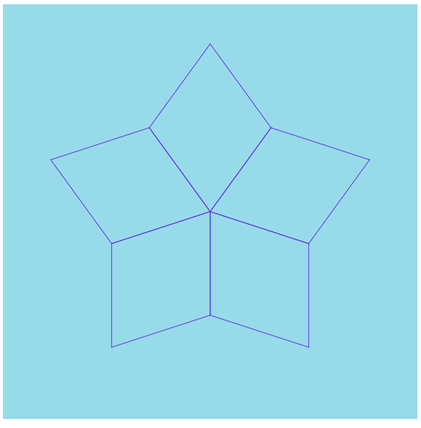
このとき変数productionを出力すると、次の文字列がコンソールに表示されます。
[+YF–ZF[—WF–XF]+]++[+YF–ZF[—WF–XF]+]++[+YF–ZF[—WF–XF]+]++[+YF–ZF[—WF–XF]+]++[+YF–ZF[—WF–XF]+]
render()関数はこれを1文字ずつ調べ、たとえば'[‘ならpush()し、’+’ならrotate(theta)、’Y’なら何せず、’-‘ならrotate(-theta)、
‘F’ならstroke(81, 61, 230)、line(0, 0, 0, -drawLength)、translate(0, -drawLength)を実行し、その結果が全体としてペンローズ・タイルになるわけです。
genの値を2、3、4、5に変えて実行すると、下図の結果が得られます。

inkscapeを使ったペンローズ・タイル
フリーのinkscapeという描画ツールを使うと、L-systemによるペンローズ・タイルが簡単に描けます(参考:「L-SYSTEMS AND PENROSE P3 IN INKSCAPE」)。
inkscapeの[エクステンション]->[レンダリング]->[Lシステム…]を開いて、[Lシステム]ダイアログボックスを表示します。
[初期状態]テキストボックスに、[X]++[X]++[X]++[X]++[X]
[置換規則]に、W=YF++ZF—-XF[-YF—-WF]++;X=+YF–ZF[—WF–XF]+;Y=-WF++XF[+++YF++ZF]-;Z=–YF++++WF[+ZF++++XF]–XF;F=
を入力します。下図を参考にそのほかの数値を入力します。
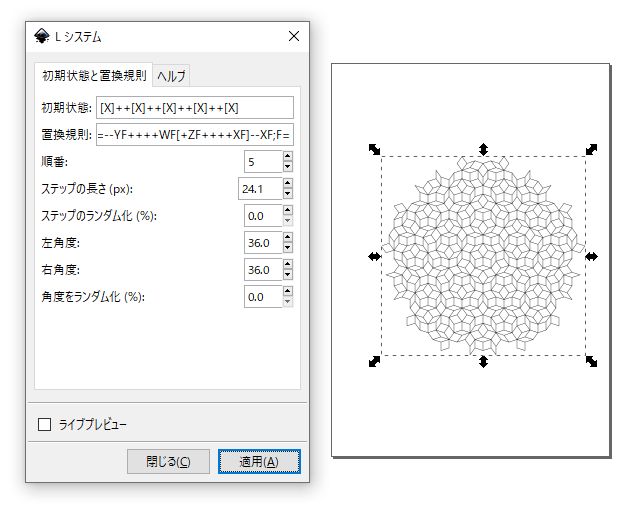
再帰的に枝分かれする木
木のような単純な構造を再帰によって描画します。枝分かれする角度は水平方向のマウス位置の関数として計算されます。マウスを左右に動かすと枝分かれの角度が変わります。ダニエル・シフマンによるProcessing向けのRecursive Treeサンプルにもとづく。
// 角度
let theta;
function setup() {
createCanvas(710, 400);
}
function draw() {
background(0);
frameRate(30);
stroke(255);
// 0度から90度の角度を、現在のマウス位置から決める
const a = (mouseX / width) * 90;
// ラジアン値に変換
theta = radians(a);
// 画面下端からツリーを開始
translate(width / 2, height);
// 120ピクセルの縦線を描く
line(0, 0, 0, -120);
// その線の上端に座標システムを移動
translate(0, -120);
// 再帰的な枝分かれを開始
branch(120);
}
// 再帰的に枝分かれする
function branch(h) {
// 枝のサイズは前のサイズの2/3
h *= 0.66;
// すべての再帰関数には必ず終了条件が必要
// ここでは、枝の長さが2ピクセル未満になったら終了
if (h > 2) {
push(); // 現在の変換状態を保存
rotate(theta); // thetaだけ座標システムを回転
line(0, 0, 0, -h); // 枝を描画
translate(0, -h); // 枝の下端に座標システムの原点を移す
branch(h); // 準備できたので、自分自身を呼び出して、2つの新しい枝を描く
pop(); // 前の行列の状態に戻す
// 同じことを繰り返すが、今度は左の枝分かれを描画
push();
rotate(-theta);
line(0, 0, 0, -h);
translate(0, -h);
branch(h);
pop();
}
}マウスを左右に動かすと、木が枝分かれして変化します。
解説
これは、毎フレーム、座標変換でキャンバス幅の真ん中に描く幹の先端を原点として、branch()関数を再帰的に呼び出して、先端から2つに分かれする枝を描くサンプルです。枝分かれするときの角度を、その時点のマウスのx位置から計算しているので、マウスを左右に動かすと、幹から先の枝ぶりがダイナミックに変化します。
再帰関数
再帰関数は、聞いたことはあるが使ったことはない、分かっているつもりだがどこで使ってよいか分からない、と多くの人が思っている類の関数です。
「再帰関数を理解するための最もシンプルな例」ページには、再帰関数を使う理由について、次のように書かれています(書籍「独学プログラマー」からの引用)。
再帰は、大きな問題を小さな問題に分割して解決する分割統治法で使われる手法で、
小さな問題は比較的楽に解決できるだろう、という点に着目しています。
(中略)
反復法で解決できるどんな問題も、再帰法に置き換えられます。
その上、再帰法はより洗練された解決法となることがあります。
上記サンプルで言うと、枝分かれする数分だけ繰り返し処理を行えば同様の結果は得られるので、それでも構わないのですが、その反復法は再帰法に置き換えられる、ということです。
そして使用するときのルールについて、次のように書かれています。
- 再帰法は、再帰終了条件を持たなければならない。
- 再帰法は、状態を変えながら再帰終了条件に進んでいかなければならない。
- 再帰法は、再帰的に関数自身を呼び出さなければならない。
これについては、上記サンプルの場合、次のように考えられます。
再帰終了条件は、if条件で使われている(h > 2)です。変数hはbranch()関数に渡される引数で、これはbranch()の最初で0.66倍に縮小されます。この値が2より大きい場合に、枝分かれが描画されます。hは小さくなっていくので、やがてこの条件に当てはまらなくなります。
状態を変えながら再帰終了条件に進んでいかなければならないというのは、branch()関数が呼び出されるたびに変数hの値に0.66が掛けられることです。具体的に言うと、branch()関数はdraw()内から、branch(120)で呼びだされつづけます。この120に0.66が掛けられるので、hは79.2になります。次にbranch()が呼び出されるときにはこの79.2がhの値として渡されるので、h *= 0.66によって、hは52.272…になります。その次に呼び出されるときは34.499、その次は22.769と、小さくなっていき、再帰終了条件にある数値2に近づいていきます。
再帰的に関数自身を呼び出さなければならないというのは、branch()関数がその定義の中でbranch(h)を呼び出しているということです。branch()関数の場合には、自分自身を2回呼び出しているので、結果は1回呼び出すよりも複雑になります。
シンプルなものから理解する
branch()関数内で2回branchを呼び出したり、マウスの移動で枝分かれを変化させたり、上記サンプルは複雑なので、最もシンプルなものから見ていきましょう。
次のコードは、キャンバスの幅の真ん中から上に120ピクセルの長さの太めの白い線を描画します。これが木の幹になります。座標変換のtranslate()関数については、「5_1:移動(translate) p5.js JavaScript」で述べています。
最後の行でtranslate(0, -120)を呼び出しているので、座標システムの原点(0, 0)はこの枝の先端に移動します。
let theta;
function setup() {
createCanvas(710, 400);
theta = radians(30);
background(200);
// 木の幹を描く
stroke(255);
strokeWeight(10);
translate(width / 2, height);
line(0, 0, 0, -120);
translate(0, -120);
}
つづいて、次のbranch()関数を定義します。ここでは、シンプルにするため、branch(h)を1回呼び出すだけです。また再帰終了条件は、サンプルのh > 2 ではなく、h > 70 です。hは79.2、52.272…、34.499…、22.769…と小さくなっていくので、hと比較する数値にこれらを目安として利用することで、再帰終了条件を早めることができます。
translate(0, -120);
// 枝を描く
branch(120);
}
function branch(h) {
h *= 0.66;
if (h > 70) {
push();
rotate(theta);
// 枝同士が区別しやすいように線の色を変える
stroke(random(255), random(255), random(255));
line(0, 0, 0, -h);
translate(0, -h);
branch(h);
pop();
}
}
下図はこの結果です。branch(120)によってbranch()関数が呼び出され、hは79.2になります。hは70より大きいので、ifのステートメントが実行されます。push()とpop()はその間にはさまれた座標変換をその場でのみ限定し、元に戻す働きがあります(「5_6:変換状態の保存と復元 p5.js JavaScript」参照)。
今座標システムの原点は幹の先端です。rotate(theta)は座標システムをtheta分(30度)時計回りに回転させます。line(0, 0, 0, -h)は、幹の先端を原点とする、30度回転した座標システムで、(0, 0)と(0, -h)を結ぶ線を描きます。これは、キャンバスの元々の座標システムから見ると、まっすぐ上に伸びた幹の先端から、30度時計回りに傾いた線に見えます。
次のtranslate(0, -h)は、次の枝の描画に備えるための処理で、座標システムの原点を枝の先端に移します。そしてbranch(h)を呼び出します。branch()関数には79.2が渡され、0.66が掛けられhは52.272になります。52.272は70より小さいので、ifに書かれたステートメントは実行されません。

h > 70 を h > 50 に変えて、branch()関数を呼び出す回数を増やします。結果は下図のようになります。

つづいて、branch()関数のpop();の下に、次のコードを追加します。
push();
rotate(-theta);
stroke(random(255), random(255), random(255));
line(0, 0, 0, -h);
translate(0, -h);
branch(h);
pop();
この追加によって、枝を描くときに枝分かれが生じ、1回のbranch()の呼び出しによって、2回branch()が呼び出されるようになります。
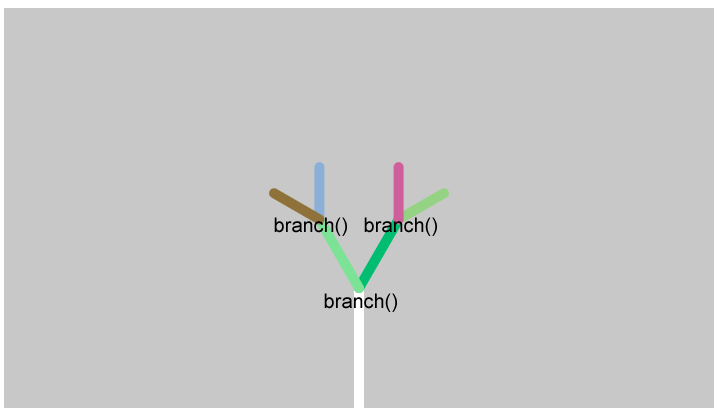
再帰終了条件のhと比較する数値を30、20に変更すると、枝分かれが増えていきます。

枝分かれのダイナミックな変化
描画される木の形をダイナミックに変化させる元になっているのは、draw()内の次の2行です。
const a = (mouseX / width) * 90;
theta = radians(a);mouseX / width は、マウスのx位置/キャンバスの幅で、その結果は、マウスが左端にあるときに0、右端にあるときに1、センターにあるときに0.5になるので、今マウスのx位置は幅の何パーセントの位置にあるかを示しているという見方ができます。これに90を掛けると、結果は0から90の間の数値になります。具体的には、マウスが左端にあるときに0、右端にあるときに90、センターにあるときに45になります。ここではこれを角度に見立てているのです。
変数thetaは、このようにしてマウスのx位置に応じて変化し、その変化はbranch()関数内の rotate(theta)と rotate(-theta)に反映されます。これによって枝分かれの角度が変わるので、描画される木全体の形が変わることになります。
マンデルブロ集合
マンデルブロ集合の単純なレンダリング。ダニエル・シフマンによるProcessing向けのMandelbrotサンプルにもとづく。
function setup() {
createCanvas(710, 400);
// デバイスピクセル(物理的な画面解像度)による違いを吸収する
pixelDensity(1);
noLoop();
}
function draw() {
background(0);
// 複素平面上にある値の範囲を設定する。
// 値の範囲を変えると、フラクタルにズームイン/アウトできる。
// すべての始まりはw。もっと高い値や低い値で試してみて。
const w = 4;
const h = (w * height) / width;
// wとhの半分の負数からスタート
const xmin = -w / 2;
const ymin = -h / 2;
// pixels[]配列に書き込みできるようにする。
// ほかの描画は行わないので、これは1回実行するだけでよい
loadPixels();
// 複素平面上の各点に対する繰り返し処理の最大数
const maxiterations = 100;
// xはxminからxmaxへ進む
const xmax = xmin + w;
// yはyminからymaxへ進む
const ymax = ymin + h;
// 各ピクセルのx,yをインクリメントする量を計算
const dx = (xmax - xmin) / (width);
const dy = (ymax - ymin) / (height);
// yを開始
let y = ymin;
for (let j = 0; j < height; j++) {
// xを開始
let x = xmin;
for (let i = 0; i < width; i++) {
// z = z^2 + c を繰り返して、zが無限に向かう(発散する)傾向があるかどうかを調べる
let a = x;
let b = y;
let n = 0;
while (n < maxiterations) {
const aa = a * a;
const bb = b * b;
const twoab = 2.0 * a * b;
a = aa - bb + x;
b = twoab + y;
// われわれの有限世界での無限は単純で、それは、無限が16だと見なすこと
if (dist(aa, bb, 0, 0) > 16) {
break; // 脱出
}
n++;
}
// 無限に到達するまでにかかった時間にもとづいて、各ピクセルを色付けする。
// 無限に到達しないのであれば、黒にする
const pix = (i + j * width) * 4;
const norm = map(n, 0, maxiterations, 0, 1);
let bright = map(sqrt(norm), 0, 1, 0, 255);
if (n == maxiterations) {
bright = 0;
}
else {
// 希望する場合には、ここでもっとしゃれた色に変えることもできる。
pixels[pix + 0] = bright;
pixels[pix + 1] = bright;
pixels[pix + 2] = bright;
pixels[pix + 3] = 255;
}
x += dx;
}
y += dy;
}
updatePixels();
}実行すると下図に示す画像が描画されます。

解説
上の図は、フラクタル好きにはたまらないとされるマンデルブロ集合をシミュレーションした描画結果です。p5.jsを扱った当サイトでは、「高校数学の美しい物語」を何度も参照させてもらっていますが、まさに数学の美しさを具現化したような美しい結果です。
とは言え、わたし自身はフラクタルマニアでも数学好きでもなく、大した知識もないので、ここでも基本から見ていくことにします。マンデルブロ集合は、複素数と呼ばれるものを扱ったもので、複素数は虚数を含むものなので、まずは虚数から見ていきましょう。
虚数
実数とは、存在するすべての数を言い、簡単に言うと物差しで測れる数値です。これに対し、虚数とは実数の反対で、現実世界では存在しない、2乗して-1になるものを言います。i^2 = -1。虚数はその前に実数で倍率をつけることができます。2i,3i。しかしその大小を比べることはできません。
![]()
複素数
複素数は、実数と虚数を混ぜたもので、実数部と虚数部からなります。a(実数部) + bi(虚数部)
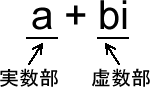
複素数の表現
複素数は平面で表すことができます。純粋な実数は横軸(実軸)上に来て、純粋な虚数は縦軸(虚軸)上に来ます。そして、複素数は平面状の1点に来るという具合です。たとえば複素数a + biは、実軸がaで、虚軸がbiの交点に来ます。この平面を複素平面と言います。
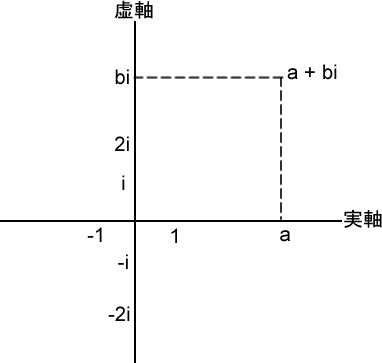
マンデルブロ集合とは?
マンデルブロ集合は、複素平面上の点の集まりで、数列の話が出てきます。
次の方程式があります。
![]()
これは、今の複素数Zを2乗してそこに複素数Cを加えたものを次のZとして、これを繰り返す、という意味です。Z=0から始めると、
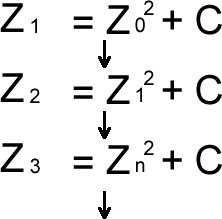
とつづきます。複素数Cの値を変えてこれを計算すると、いくつかのCの値では、Zの値が増加しつづけ(発散し)、別のいくつかのCの値では、Zの値が小さい2虚数の間を往復する(発散しない)ということを見つけた人がいました。それはブノワ・マンデルブロその人でした。
この発散しない複素数Cの値を複素平面上に点で表したものがマンデルブロ集合です。
計算方法
JavaScriptでは次のようにして計算できます。

JavaScriptでは虚数はサポートされませんが、シミュレーションすることはできます。
以下はサンプルを簡易化したコードです。キャンバスにマンデルブロ集合を描くとともに、plotly.jsを使って複素平面上にC値をプロットしています。
let startX;
let startY;
let scale;
// 繰り返し回数 これを1,2,4,8,16...に変えてみる
const iteration = 16;
const xArray = [];
const yArray = [];
function setup() {
const canvas = createCanvas(710, 400);
canvas.parent('sketch-holder');
// -3と-1.5あたりの開始と幅の5/1程度のスケールで、全体がうまく収まる
startX = -3.0;
startY = -1.5;
scale = 5 / width;
// 左上部にズームイン
//startX = -2.0;
//startY = -1.0;
//scale = 2.0 / width;
// コブにズームイン => コブの周りに小さなコブが多数ある
// iterationを300にする
//startX = -0.7;
//startY = -1.0;
//scale = 1.15 / width;
// pixels配列を使用するので、アクセスできるようにする。
loadPixels();
// 高解像度ディスプレイ対応
pixelDensity(1);
// draw()を1回だけ呼び出す
noLoop();
}
function draw() {
background(0);
// キャンバスの高さ分だけ繰り返す
for (let j = 0; j < height; j++)
// キャンバスの幅分だけ繰り返す
for (let i = 0; i < width; i++) {
// 計算対象とする数値
const a = startX + i * scale;
const b = startY + j * scale;
// whileループでaとbを操作し、この時点のaとbを使用するので、
// 変数xとyにメモして値を操作するのはxとyにする
let x = a;
let y = b;
let n = 0; // 繰り返し回数のカウンタ
// iteration未満まで繰り返す
while (n < iteration) {
// Z^2 + Cの計算に必要な部分を求める
const xx = x * x; // (x^2 - y^2 +a) + (2xy + b)i のx^2
const yy = y * y; // (x^2 - y^2 +a) + (2xy + b)i のy^2
const twoxy = 2 * x * y; // (x^2 - y^2 +a) + (2xy + b)i の2xy
// 新しいxとyを計算し、発散するかどうかを調べる
x = xx - yy + a; // (x^2 -y^2 + a)をxに代入
y = twoxy + b; // (2xy + b)をyに代入
// 発散したらnをインクリメントしない
if (x * x + y * y > 16) {
break
}
// 新しいxとyでさらに繰り返す
n++;
}
// 今、対象としているピクセルを特定
const pic = (i + j * width) * 4;
// 拡散していないなら、今の対象ピクセルの色を白に
if (n >= iteration) {
pixels[pic + 0] = 255; // R
pixels[pic + 1] = 255; // G
pixels[pic + 2] = 255; // B
pixels[pic + 3] = 255; // alpha
// 拡散していたら、今の対象ピクセルの色を黒に
}
else {
pixels[pic + 0] = 0
pixels[pic + 1] = 0;
pixels[pic + 2] = 0;
pixels[pic + 3] = 255;
}
// 実数部(x^2 -y^2 + a)をxに、虚数部(2xy + b)をyにしてグラフに描画
xArray.push(x);
yArray.push(y);
}
// pixels配列を更新してその内容をキャンバスに描画
updatePixels();
// グラフに描く
plot(xArray, yArray);
}下図はこの実行結果です。
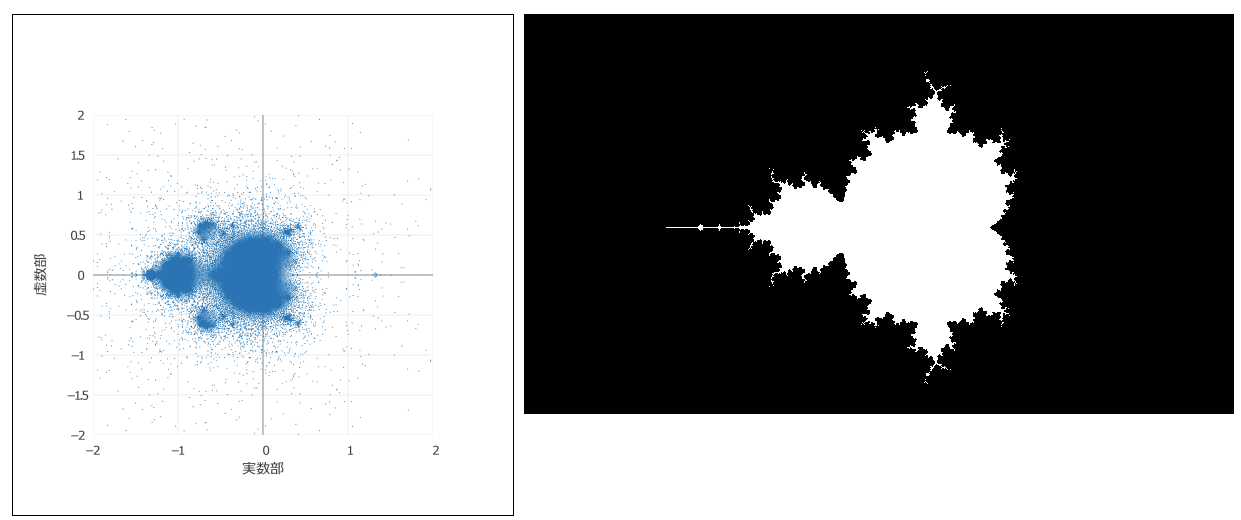
iterationの値を変えると、形が変わります。下図は右から2,4,8を代入して実行した結果です。

またstartXとstartY、scale変数を操作すると、描かれる図形の位置を変えたり、特定の位置にズームインすることができます。下図は、iteration=16、startX = -2.0、startY = -1.0、scale = 2.0 / widthにして、左上にズームインした結果です。
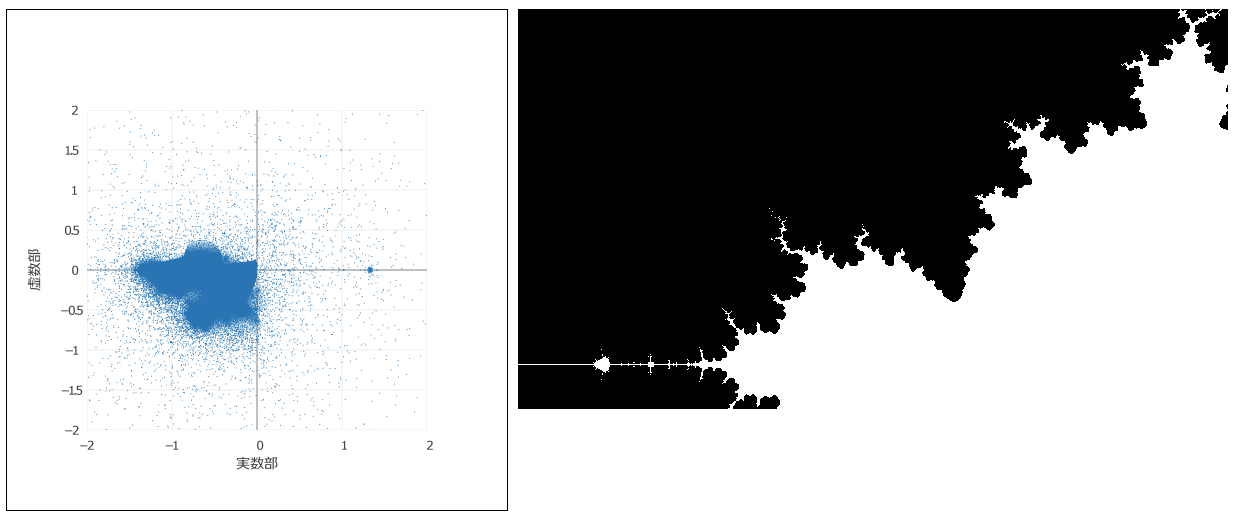
さらに、iteration=100,startX = -0.7,startY = -1.0,scale = 1.15 / width にして実行すると、コブにズームインできます。コブの周りには小さなコブがたくさんあることが分かります。

なんでこうなるのかはさっぱり分かりません。また偉い先生に説明されても理解できないでしょう。何とも摩訶不思議な「数学の美しさ世界」です。
リファレンスメモ
説明
表示ウィンドウ(キャンバス)のピクセルデータをpixels[]配列に読み込む。pixels[]から値を読み取ったり値を書き込むときにはその前にこの関数を呼び出す必要がある。変更は、set()の使用か、 pixels[]への直接の操作によってのみ発生する点に注意。p5.Imageにもよく似たloadPixels()がある。
説明
表示ウィンドウ(キャンバス)をpixels[]配列のデータで更新する。loadPixels()との組み合わせで使用する。pixels[]配列からデータを読み取りたいだけの場合には、updatePixels()を呼び出す必要はなく、更新は変更を適用するときのみ必要になる。updatePixels()は、ピクセルの配列を操作するか、set()を呼び出したときにつねに呼び出すようにする。変更はset()かpixels[]配列への直接の操作によってのみ発生する。p5.Imageにもよく似たupdatePixels()がある。
説明
表示ウィンドウのすべてのピクセルを含むUint8ClampedArray(要素の値が0-255の範囲に切り詰められる8ビット符号なし整数の配列)。値は数値。この配列は表示ウィンドウの4倍のサイズ4になる(pixelDensity()による要因も関係する)。要素の数値(0-255)は順に、各ピクセルのR,G,B,A値を表し、各行を左から右に進んでから、各列を下に進む。Retinaやそのほかの高密度ディスプレイで表示する場合には、pixels[]の要素数が多くなる(ピクセル密度^2の要因により)。たとえば100 x 100のイメージのpixels[]の要素数は40,000だが、Retinaでは160,000になる。
pixels[]の最初の4つの値(インデックス0-3)は、キャンバスの(0,0)にあるピクセルのR,G,B,A値になる。2つめの値(インデックス4-7)は、キャンバスの(1,0)にあるピクセルのR,G,B,A値になる。一般化すると、(x,y)にあるピクセルの値を設定するには次のようにする。、
let d = pixelDensity();
for (let i = 0; i < d; i++) {
for (let j = 0; j < d; j++) {
// loop over
index = 4 * ((y * d + j) * width * d + (x * d + i));
pixels[index] = r;
pixels[index + 1] = g;
pixels[index + 2] = b;
pixels[index + 3] = a;
}
}この方法は複雑だが、どんなピクセル密度でも動作する柔軟性がある。set()はどんなピクセル密度であっても、任意の(x,y)に関するpixels[]の適切な値を自動的に設定するが、pixels[]に多くの変更が行われる場合には、パフォーマンスが遅くなるかも知れない。
pixels[]にアクセスるするにはその前に、loadPixels()関数を使ってデータを読み込み、配列データを変更したら、updatePixels()関数を使ってその変更を更新する必要がある。
pixels[]は標準のJavaScript配列ではないことには注意が要る。これは、slice()やarrayCopy()といった標準的なJavaScript関数が動作しないことを意味する。p5.Imageにもよくにたpixelsがある。
説明
高ピクセル密度ディスプレイのピクセルスケーリングを設定する。ピクセル密度はデフォルト設定によって、ディスプレイ密度に一致するよう設定されるので、これをオフにするにはpixelDensity(1)を呼び出す。pixelDensity()に引数を与えないで呼び出すと、スケッチの現在のピクセル密度を返す。
コッホ曲線
単純なフラクタル、コッホ雪片をレンダリングします。再帰レベルを連続して描画します。ダニエル・シフマン作
sketch.js
let k;
function setup() {
createCanvas(710, 400);
frameRate(1); // ゆっくりアニメーションする
k = new KochFractal();
}
function draw() {
background(0);
// 雪片を描画
k.render();
// 繰り返す
k.nextLevel();
// 5回より多くは行わない
if (k.getCount() > 5) {
k.restart();
}
}KochLine.js
// フラクタルとなる1本の線分表すクラス
// コッホアルゴリズムに従って、線に沿ってp5.Vectorを計算するメソッドが含まれる
class KochLine {
constructor(a, b) {
// 2つのp5.Vector。
// startは"左"のp5.Vector
// endは"右"のp5.Vector
this.start = a.copy();
this.end = b.copy();
}
display() {
stroke(255);
line(this.start.x, this.start.y, this.end.x, this.end.y);
}
kochA() {
return this.start.copy();
}
// これは簡単、startからendまでの1/3
kochB() {
let v = p5.Vector.sub(this.end, this.start);
v.div(3);
v.add(this.start);
return v;
}
// これは複雑。p5.Vectorの場所の計算には正三角形が必要
kochC() {
let a = this.start.copy(); // startから開始
let v = p5.Vector.sub(this.end, this.start);
v.div(3);
a.add(v); // ポイントBに移動
v.rotate(-PI / 3); // 反時計回りに60度回転
a.add(v); // ポイントCに移動
return a;
}
// これも簡単、startからendまでの2/3
kochD() {
let v = p5.Vector.sub(this.end, this.start);
v.mult(2 / 3.0);
v.add(this.start);
return v;
}
kochE() {
return this.end.copy();
}
}KochFractal.js
// 線分のリストを雪片パターンで管理するクラス
class KochFractal {
constructor() {
this.start = createVector(0, height - 20); // 開始用のp5.Vector
this.end = createVector(width, height - 20); // 終了用のp5.Vector
this.lines = []; // すべての線を追跡するための配列
this.count = 0;
this.restart();
}
nextLevel() {
// 配列に含まれるすべての線について、
// 新しい配列内に線を4つ作成する
this.lines = this.iterate(this.lines);
this.count++;
}
restart() {
this.count = 0; // カウントをリセット
this.lines = []; // 配列を空にする
// 最初の線を追加する(一方のp5.Vectorからもう一方のp5.Vectorへの線)
this.lines.push(new KochLine(this.start, this.end));
}
getCount() {
return this.count;
}
// これは簡単、全部を線を描画する
render() {
for (let i = 0; i < this.lines.length; i++) {
this.lines[i].display();
}
}
// ここは**魔法**が起こる場所
// ステップ1:空の配列を作成
// ステップ2:今配列にあるすべての線について、
// - コッホアルゴリズムにもとづいて4つの線分を計算する
// - 4つの線分を新しい配列に追加する
// ステップ3:新しい配列を返す。これが、構造を示す線分のリストになる
// これを何度も繰り返すと、各線は4つに分かれ、その4つも4つの線に分かれ、...ということになる。
iterate(before) {
let now = []; // 空の配列を作成
// lines配列に含まれるKochLineオブジェクトを走査
for (let i = 0; i < this.lines.length; i++) {
let l = this.lines[i];
// 5つのコッホp5.Vectorを計算する(これはKochLineオブジェクトで行う)
let a = l.kochA();
let b = l.kochB();
let c = l.kochC();
let d = l.kochD();
let e = l.kochE();
// すべてのp5.Vector間の線分を作成し追加する
now.push(new KochLine(a, b));
now.push(new KochLine(b, c));
now.push(new KochLine(c, d));
now.push(new KochLine(d, e));
}
return now;
}
}解説
コッホ曲線とは、スウェーデンの数学者ヘルゲ・フォン・コッホが考案したフラクタル図形で、線分を3等分し、分割した2点を頂点とする正三角形の作図を無限に繰り返すことで得られます(ウィキペディア「コッホ曲線」)。
コッホ曲線は次のように作成します(「コッホ曲線の作成手順」)
- 線分を引く。(ステップ0、下図の(1))
- 線分を3等分し、中央の線分を1辺とする正三角形を描き、下の辺を消す。(ステップ1、下図の(2))
- 得られた4つの線分に対して同じ操作を繰り返す。(ステップ2、下図の(3))
- 得られた16の線分に対して同じ操作を繰り返す。(ステップ3、下図の(4))
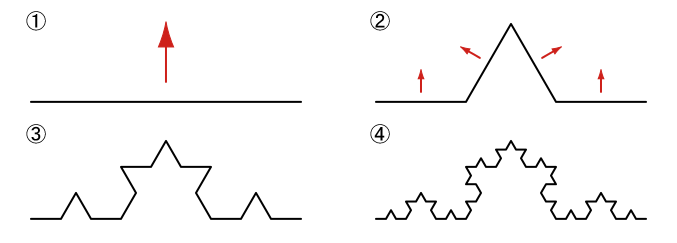
この作図はKochLineクラスのメソッド(kochA()やkochB()など)が行っています。では、KochLineクラスからこれらのメソッドを取り出して単純化し、その動作内容を確認してみましょう。
各メソッドは、同じ名前で、引数に開始ベクトルと終了ベクトルを受け取るよう、次のように書き換えます。drawLine()関数はdisplay()メソッドの置き換えです。
// startVとendVを結ぶ線を描く
function drawLine(startV, endV) {
line(startV.x, startV.y, endV.x, endV.y);
}
function kochA(startV, endV) {
return startV.copy();
}
function kochB(startV, endV) {
let v = p5.Vector.sub(endV, startV);
v.div(3);
v.add(startV);
return v;
}
function kochC(startV, endV) {
let a = startV.copy();
let v = p5.Vector.sub(endV, startV);
v.div(3);
a.add(v);
v.rotate(-PI / 3);
a.add(v);
return a;
}
function kochD(startV, endV) {
let v = p5.Vector.sub(endV, startV);
v.mult(2 / 3.0);
v.add(startV);
return v;
}
function kochE(startV, endV) {
return endV.copy();
}setup()関数は次のようにします。変数startとendにcreateVector()を使って値を代入している2行は、KochFractalクラスのコンストラクタ関数内のコードに相当します。
let start;
let end;
function setup() {
createCanvas(710, 400);
start = createVector(0, height - 20);
end = createVector(width, height - 20);
background(40);
const v1 = kochA(start, end);
const v2 = kochB(start, end);
// 白線
stroke(255, 255, 255);
drawLine(v1, v2);
}startは(0,380)で、endは(710,380)の値を持つp5.Vectorオブジェクトです。名前にkochの付く関数にはすべてこの2つを渡します。
kochA()関数
kochA()関数は受け取ったstartVをただコピーして返すだけの関数です。
function kochA(startV, endV) {
return startV.copy();
}しかしこのコピーには、渡されたstartVがp5.Vectorオブジェクトでないときにエラーを発生させる、という隠れた働きが仕込まれています。startVが必ずp5.Vectorオブジェクトであるのならコピーする必要はありませんが、その保証はありません。もし渡されたものをそのまま返すだけにすると、p5.Vectorオブジェクトでない場合もそのまま返されてしまうので、その後のプログラムが正常に機能しなくなります。
kochA(start, end)からは(0,380)が返されるので、これが変数v1に割り当てられます。
kochB()関数
kochB()にも(0,380)と(710,380)を渡します。
function kochB(startV, endV) {
let v = p5.Vector.sub(endV, startV);
v.div(3);
v.add(startV);
return v;
}kochB()では、(710,380)から(0, 380)を引いた(710,0)を変数vとします。これは(0, 380)から(710,380)までの線の長さに相当し、上記「コッホ曲線の作成手順」のステップ0の線分です(以降ではこれを”全長”と呼ぶことにします)。
そしてこれを3等分し((710,0) / 3 = (236.66, 0)、「コッホ曲線の作成手順」のステップ1)、それに(0, 380)を加えます((236.66, 0) + (0,380) = (236.66, 380))。これは、startVからendVに向けて、全長の1/3だけ進んだポイントに当たります。
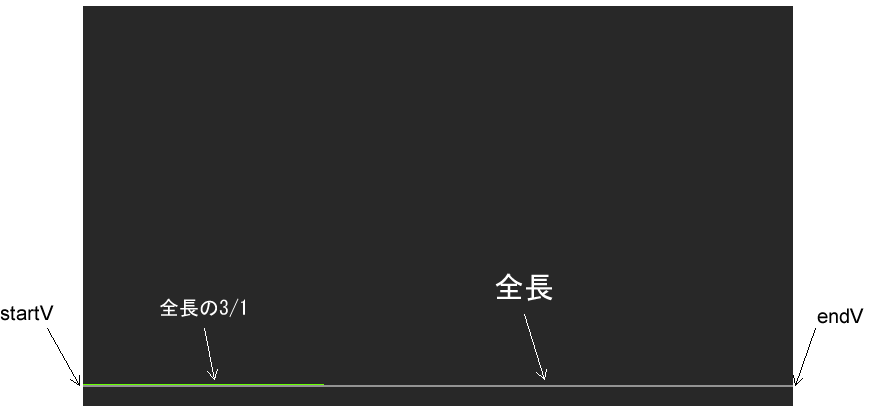
kochB(start, end)からは(236.66, 380)が返されるので、これが変数v2に割り当てられます。
線の色を白にして、drawLine()関数にv1とv2を渡すと、下図の結果が得られます。
// 白線
stroke(255, 255, 255);
drawLine(v1, v2);
kochC()関数
つづいて、kochC()関数を呼び出してv3を得、線を赤に変えて、v2からv3までの線を描きます。
const v3 = kochC(start, end);
// 赤線部
stroke(255, 0, 0);
drawLine(v2, v3);kochC()関数にもstartとendを指定しているので、(0,380)と(710,380)が渡されます。
function kochC(startV, endV) {
let a = startV.copy();
let v = p5.Vector.sub(endV, startV);
v.div(3);
a.add(v);
v.rotate(-PI / 3);
a.add(v);
return a;
}kochC()関数は一見複雑そうに見えますが、途中までは実質的にkochB()と同じです。1行めでは受け取ったstartVがp5.Vectorでなかった場合に確実にエラーが発生するようにp5.Vector.copy()メソッドを使用しています。そして全長を得て、それを3等分します。ここまではkochB()と同じです。ただし変数vとaを使い分けている点に注目してください。
次に、全長を3等分したvを反時計回りに60度回転させます。これはどういうことかと言うと、下図に示す線分V1V2をv1を中心に反時計回りに60度回転させる、ということです。
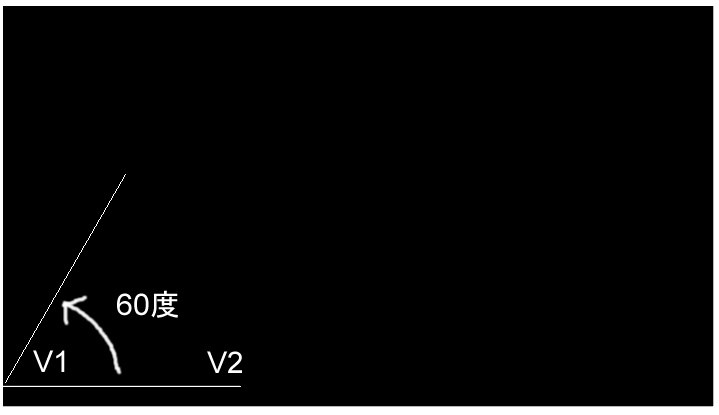
60度は正三角形の内角であり、この回転は上記「コッホ曲線の作成手順」のステップ1に相当します。そしてaに、回転させたvを足すと、下図の赤線のベクトルになります。
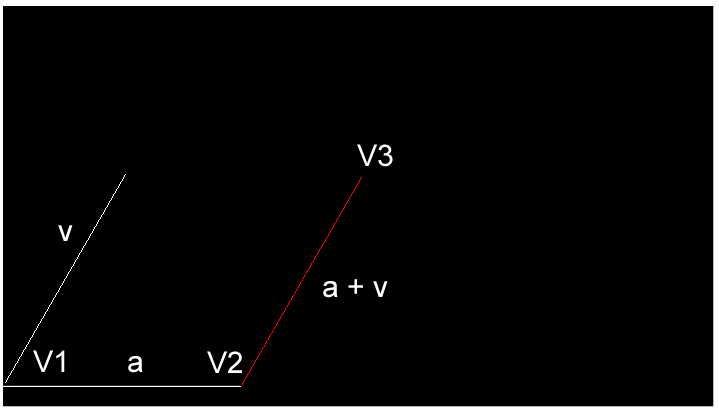
ここまでの描画結果は次のようになります。
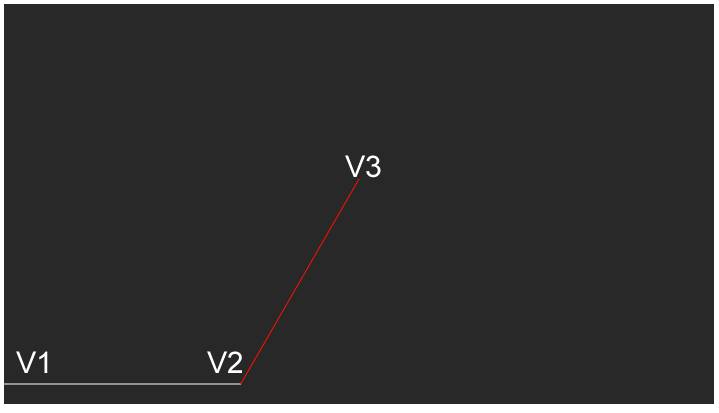
kochD()関数
つづいて、kochD()を使ってv4を得て、黄色の線を引きます。kochD()にもこれまでと同様、startとend、つまり(0,380)と(710,380)を渡します。
const v4 = kochD(start, end);
// 黄線部
stroke(255, 255, 0);
drawLine(v3, v4);kochD()は次の関数です。
function kochD(startV, endV) {
let v = p5.Vector.sub(endV, startV);
v.mult(2 / 3.0);
v.add(startV);
return v;
}vはこれまでと同様、全長です。ここではそれに2/3を掛けています。ここまでの流れから言うと、kochB()関数で得たV2からendVの方向に全長の1/3だけ進めばよいわけですが、koch関数ではその方法は取りません。具体的にいうと、どのkoch関数も、同じstartとendを使って、与えられた答えを返そうとします。
全長の2/3にstartVを足すと、下図のV4になります。これをv3と線でつなぐと黄色の線になります。
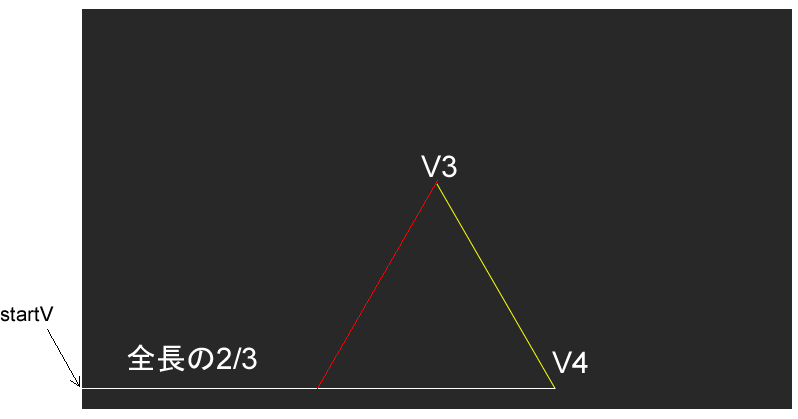
kochE()関数
kochE()関数は受け取ったendVのコピーを返します。この関数にもkochA()と同じ機能が隠されています。
function kochE(startV, endV) {
return endV.copy();
}kochE()関数が返すv5を使って次のように青線を引きます。
const v5 = kochE(start, end);
// 青線部
stroke(0, 255, 255);
drawLine(v4, v5);ここまでを全部実行すると、次の結果が得られます。
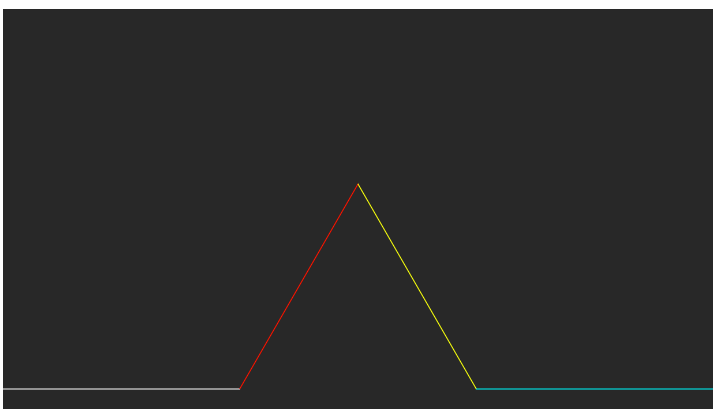
正三角形であるかどうかの確認
v2とv3、v4を結んでできる三角形は、辺v2v3が全長の1/3で、辺v2v4も全長の1/3(辺v1v4が全長の2/3)なので二等辺三角形です。またv3-v2-v4を結んでできる内角は60度なので、この二等辺三角形は正三角形だと言えます。
それは次のコードで確認できます。ただし暫定的に、各koch関数内のvを正規化する必要があります(v.normalize())。
// 正三角形かどうか
print(v2.mag()); // 380ほど
print(v3.mag()); // 380ほど
print(v4.mag()); // 380ほど
// V2
const a = atan2(v2.y - v3.y, v2.x - v3.x);
print(degrees(a)); // 120ほど。これは180-120 = 60度
// v3
const b = atan2(v4.y - v3.y, v4.x - v3.x);
print(degrees(b)); // 60ほど
次のレベルへ
ここまでで「コッホ曲線の作成手順」の図2までが描画できました。次は「得られた4つの線分に対して同じ操作を繰り返す。(ステップ2、下図の(3))」です。これは基本的には、各koch関数に、次のレベルのstartとendを、つまり線分の両端を表すp5.Vectorを渡すことで実現できます。
たとえば次のコードでは、startにv1を、endにv2を渡しています。したがって、v1とv2を両端とする線分について、同様の描画が行えます。
start = v1;
end = v2;
const v6 = kochA(start, end);
const v7 = kochB(start, end);
stroke(255, 255, 255);
drawLine(v6, v7);
const v8 = kochC(start, end);
stroke(255, 0, 0);
drawLine(v7, v8);
const v9 = kochD(start, end);
stroke(255, 255, 0);
drawLine(v8, v9);
const v10 = kochE(start, end);
stroke(0, 255, 255);
drawLine(v9, v10);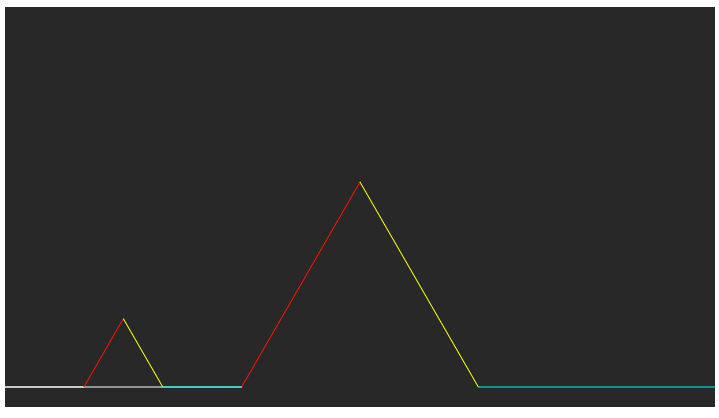
同様に、start = v2、end = v3にすると、下図の左が、start = v3、end = v4にすると、下図の右が描画できます。

ただしここまで行ってきた、5種類のkoch関数を呼び出し、その値を変数に入れて、1本ずつ線を引いていくやりかたでは、おのずと限界があります。力技でできなくもありませんが、もっと手数のかからない方法を考えるべきです。その最たるものが、前述したサンプルのコード(KochLineクラスとKochFractalクラス)だと言えるでしょう。