10：インタラクション (Interaction)

インタラクションとは、「インタラクションの用語説明」ページに、次のように説明されています。

インタラクションとは英語の「 inter（相互に）」と「action（作用）」を合成したもので、その基本は「人間が何かアクション(操作や行動)をした時、そのアクションが一方通行にならず、相手側のシステムなり機器がそのアクションに対応したリアクションをする」ということです。

こちょこちょ

“tickle”という文字にカーソルを重ねると、文字が小刻みに動きます。画面外で”こちょこちょ”できる場合もあります。

let message = 'tickle',
    font,
    bounds, // テキストの境界ボックスのx, y, w, hを保持する
    fontsize = 60,
    x,
    y; // テキストのxとy座標

// 使用するフォントファイルをプリロード
function preload() {
    // https://p5js.org/reference/#/p5/loadFont
    font = loadFont('assets/SourceSansPro-Regular.otf');
}

function setup() {
    createCanvas(710, 400);

    // フォントの設定
    textFont(font);
    textSize(fontsize);

    // 最初にセンターに配置できるように、テキストの幅と高さを得る
    bounds = font.textBounds(message, 0, 0, fontsize);
    x = width / 2 - bounds.w / 2;
    y = height / 2 - bounds.h / 2;
}

function draw() {
    // 半透明 => 残像が残る
    background(204, 120);

    // テキストを黒で描画し、境界ボックスを得る
    fill(0);
    text(message, x, y);
    bounds = font.textBounds(message, x, y, fontsize);

    // マウスが境界ボックスの中にあるかどうか調べ、もしそうなら小刻みに動かす
    if (
        mouseX >= bounds.x &&
        mouseX <= bounds.x + bounds.w &&
        mouseY >= bounds.y &&
        mouseY <= bounds.y + bounds.h
    ) {
        x += random(-5, 5);
        y += random(-5, 5);
    }
}

解説

このサンプルのインタラクションは、ユーザーが行うマウス移動というアクションに対し、マウスカーソルが文字の上に重なったらプログラムが文字を小刻みに動かすというリアクションを行う、ということです。これを可能にしているのは、p5.FontのtextBounds()メソッドです。

p5.Font.textBounds()は、現在設定されているフォントを使って、文字を描画したら、どれだけの領域を占めるのかを示す境界ボックス(バウンディングボックス)を返します。境界ボックスは、描画される文字のxとy位置、幅と高さの値を持ったオブジェクトです。

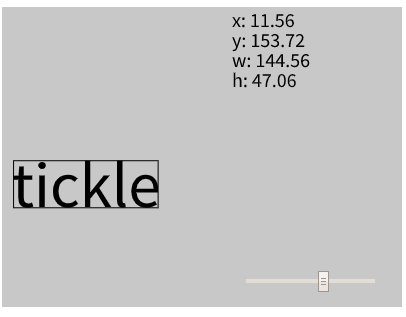
次のコードは、loadFont()関数で取得したp5.Fontオブジェクト(変数font)からtextBounds()を呼び出して、境界ボックスの情報を表示します。p5.dom.jsのスライダ操作でフォントサイズが変わるので、境界ボックスの位置やサイズも変わります。

const message = 'tickle';
let font, bounds, x, y, fontsize;

let slider;

function preload() {
    font = loadFont('assets/SourceSansPro-Regular.otf');
}

function setup() {
    createCanvas(400, 300);
    // text()で使用するフォントを設定
    textFont(font);
    x = 10;
    y = height - 100;
    slider = setSlider();
}

function draw() {
    background(200);
    // スライダの今の値を得る
    const val = slider.value();
    // その値をtext()で描画する文字サイズに設定
    textSize(val);
    // 文字を描画
    text(message, x, y);
    // 現在の境界ボックスを得る
    bounds = font.textBounds(message, x, y, val);
    noFill()
        // 現在の境界ボックスを矩形で描画
    rect(bounds.x, bounds.y, bounds.w, bounds.h);
    fill(0);
    // 境界ボックスの情報を描画
    showInfo();
}

function setSlider() {
    const s = createSlider(10, 100, 30.1);
    s.position(250, 280);
    return s;
}

function showInfo() {
    textSize(20);
    text('x: ' + bounds.x, 230, 20);
    text('y: ' + bounds.y, 230, 40);
    text('w: ' + bounds.w, 230, 60);
    text('h: ' + bounds.h, 230, 80);
}

リファレンスメモ

textBounds()

説明

このフォントを使って与えられたテキスト文字列を描画するときの、緊密な境界ボックスを返す(現在は１行の文字列のみがサポートされる)。

シンタックス

textBounds(line, x, y, [fontSize], [options])

パラメータ

line 文字列：１行のテキスト
x 数値：x位置
y 数値：y位置
fontSize 数値：使用するフォントサイズ(オプション)。デフォルトは12。
options オブジェクト：opentypeのオプションオプション)。opentypeフォントは、アライメントとベースラインオプションが含まれる。デフォルトは’LEFT’と’alphabetic’

戻り

オブジェクト：x,y,w,hプロパティを持つ矩形オブジェクト

p5.jsでのテキストやフォントの扱い方やそれに関係する関数などについては、「6_4：フォント p5.js JavaScript」や「6_6：カスタムフォントの使用 p5.js JavaScript」、「11：テキストと文字表現 Creative Coding p5.js」で述べています。

ついて来る１

線のセグメント(線分)が、マウスカーソルによって、行きつ戻りつします。キース・ピータースのコードにもとづく。

let x = 100,
    y = 100,
    angle1 = 0.0,
    segLength = 50;

function setup() {
    createCanvas(710, 400);
    strokeWeight(20.0);
    stroke(255, 100);
}

function draw() {
    background(0);

    dx = mouseX - x;
    dy = mouseY - y;
    angle1 = atan2(dy, dx);
    x = mouseX - cos(angle1) * segLength;
    y = mouseY - sin(angle1) * segLength;

    segment(x, y, angle1);
    ellipse(x, y, 20, 20);
}

function segment(x, y, a) {
    push();
    translate(x, y);
    rotate(a);
    line(0, 0, segLength, 0);
    pop();
}

解説

このサンプルの参考元の作成者キース・ピータースは、Flashで使われたActionScript3.0言語によるアニメーションについて詳しく解説した書籍「ActionScript 3.0 アニメーション」の著者です(ちなみに翻訳者はわたしです)。

サンプルのdraw()関数では、次のコードが使用されています。

 dx = mouseX - x;
 dy = mouseY - y;
 angle1 = atan2(dy, dx);

これは、２辺の長さが分かっているときに、直角三角形を想定して角度を求める方法です。ここで使われているatan2()は、「８：数学(Math)」の「アークタンジェント」サンプルで出てきた関数です。

atan2()は、下図に示すように、直角三角形の、斜辺でない２辺の長さが分かっていて、角度を知りたいときに使用します。

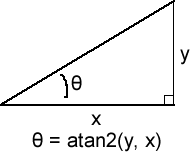
たとえば上図で、yが1、xが√3だとすると、角度θは次のコードで計算できます(参考「【三平方の定理】 特別な直角三角形の3辺の比」)

const angle = atan2(1, sqrt(3));
print(degrees(angle));  // 30度 

したがって、上記のdraw()内の３行は、下図の角度angle1を求めているということになります。

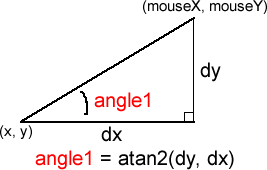
atan2()で求めた角度(angle1)はこの後、segment()関数に渡しますが、その前に、xとyを決める次の２行で使っています。このxとyは描画する円の中心座標になります。

x = mouseX - cos(angle1) * segLength;
y = mouseY - sin(angle1) * segLength;
...
ellipse(x, y, 20, 20);

cos(angle1)にsegLength(=50)を掛けた数値をmouseXから引き、それをxに割り当て、sin(angle1)にsegLength(=50)を掛けた数値をmouseYから引き、それをyに割り当て、そのxとyを中心とする円を描く、というのは一体何を意味しているのでしょう？

分かりやすくするために、setup()関数内を次のように書き換えます。

createCanvas(710, 400);
strokeWeight(3);
stroke(255);
noFill();

そしてdraw()関数のxとyを決めた次の行に、(mouseX, mouseY)を中心とする半径segLengthの円を描きます。

x = mouseX - cos(angle1) * segLength;
y = mouseY - sin(angle1) * segLength;
// 挿入
ellipse(mouseX, mouseY, segLength * 2);

コードを実行すると、次の結果が得られます。

マウスカーソルを上下左右に動かしてみると分かりますが、ellipse(x, y, 20, 20)で描画する小さな円の中心は、ellipse(mouseX, mouseY, segLength * 2)で描画する大きな円の円周上につねにあります。これは、(x, y)が大きな円の円周上の点だということです。言い方を変えると、(x,y)はつねにマウスカーソルからsegLengthだけ離れているということです。

マウスカーソルの動きに対して、小さな円は、一定の決まりに応じて、大きな円の円周上を動いているように見えます。これを行っているのが、cos(angle1)のxへの、sin(angle1)のyへの代入です。そして一定の決まりとはatan2()が計算した角度です。

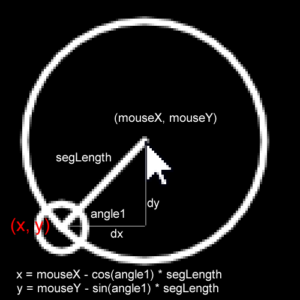
segment()関数は、(x, y)を原点としてangle1度だけ回転し、その後原点である(x, y)から真右に向けて長さsegLengthの線を引く関数です。

function segment(x, y, a) {
    push();
    // (x, y)=>円の中心に座標システムの原点を移動
    translate(x, y);
    // a度だけ回転
    rotate(a);
    // (0,0)から(50,0)まで線を描く
    line(0, 0, segLength, 0);
    pop();
}

segment()関数にangle1を指定する代わりに、radians(0)、radians(45)、radians(90)を指定すると、引かれる線の角度は次のように変わります。

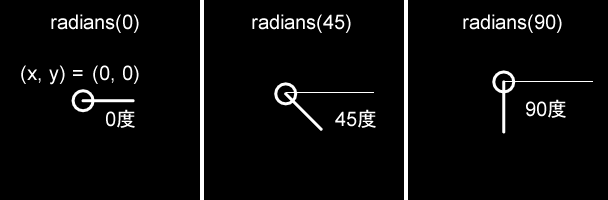
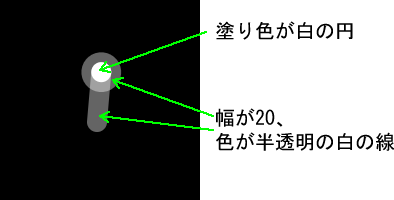
最後に、描かれるシェイプは少し複雑なように見えますが、ただの白い円と、半透明の白の太い線の組み合わせです。strokeWeight(20.0)によって、線の幅が20になり、stroke(255, 100)によって、線の色が半透明(100)の白になります。

ついて来る２

２つのセグメントから成るアームがカーソル位置について来ます。セグメント間の相対角度はatan2()で計算され、位置はsin()とcos()で計算されます。キース・ピータースのコードにもとづく。

let x = [0, 0];
let y = [0, 0];

const segLength = 50;

function setup() {
    createCanvas(710, 400);
    strokeWeight(20.0);
    stroke(255, 100);
}

function draw() {
    background(0);
    dragSegment(0, mouseX, mouseY);
    dragSegment(1, x[0], y[0]);
}

function dragSegment(i, xin, yin) {
    const dx = xin - x[i];
    const dy = yin - y[i];
    const angle = atan2(dy, dx);
    x[i] = xin - cos(angle) * segLength;
    y[i] = yin - sin(angle) * segLength;
    segment(x[i], y[i], angle);
}

function segment(x, y, a) {
    push();
    translate(x, y);
    rotate(a);
    line(0, 0, segLength, 0);
    pop();
}

解説

これはまさに、関数の特徴をいかしたプログラミングの妙味とも言えるサンプルです。

パラメータ変数iとxin、yinを受け取るdragSegment()関数は、値の取得と設定に配列を使っているものの、前の「ついて来る１」のdraw()関数内のコードとほとんど同じです。dragSegment()はつまり、複数の線分(セグメント)を作成するために、「ついて来る１」のdraw()関数からコードを取り出し、関数にしたものなのです。

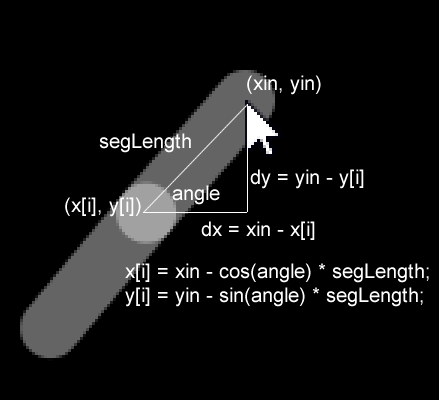
上図はdragSegment()関数の働きを示そうとした図です。dragSegment()の１回めの呼び出し、dragSegment(0, mouseX, mouseY)では、xinとyinがmouseX, mouseYとして実行され、配列のx[0]とy[0]に結果が入れられます。これにより、上図の上の線分が描画されます。

dragSegment()の１回めの呼び出し、dragSegment(1, x[0], y[0])では、xinとyinがx[0]とy[0]として実行されます。今x[0]とy[0]には、下図の上の線分の描画で使った値が入っています。計算の結果はx[1]とy[1]に入ります。これにより上図の下の線分が描画されます。

サンプルを実行しマウスを移動させてみると、線分が中折れするときがあるので、何やら複雑な処理がしてあるのかと思われるかもしれませんが、実際には、知らされた線分の開始位置を使って終了位置を計算して線分を描き、次の線分のために終了位置を保存する、という作業を繰り返しているだけです。１つめの線分は自分の後に描かれる線分があることを知らず、２つめの線分も自分の前に線分が描かれていることを知りません。

このサンプルは、dragSegment()とsegment()関数が柔軟な書き方で作成されているので、線分はいくつでも増やせます。次のように配列xとyを変更し、dragSegment()を呼び出せば、３つめの線分が作成できます。

let x = [0, 0, 0];
let y = [0, 0, 0];
...
dragSegment(2, x[1], y[1]);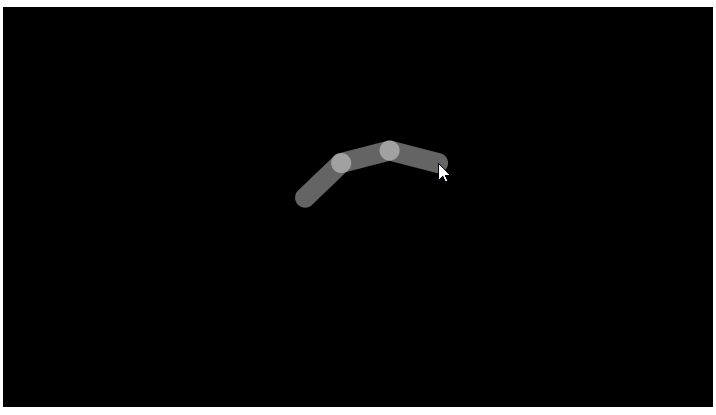

ついて来る３

複数のセグメントから成る線がマウスについて来ます。セグメントから次のセグメントへの相対角度はatan2()で計算され、次のセグメントの位置はsin()とcos()で計算されます。キース・ピータースのコードにもとづく。

let x = [],
    y = [],
    segNum = 20,
    segLength = 18;

for (let i = 0; i < segNum; i++) {
    x[i] = 0;
    y[i] = 0;
}

function setup() {
    createCanvas(710, 400);
    strokeWeight(9);
    stroke(255, 100);
}

function draw() {
    background(0);
    dragSegment(0, mouseX, mouseY);
    for (let i = 0; i < x.length - 1; i++) {
        dragSegment(i + 1, x[i], y[i]);
    }
}

function dragSegment(i, xin, yin) {
    const dx = xin - x[i];
    const dy = yin - y[i];
    const angle = atan2(dy, dx);
    x[i] = xin - cos(angle) * segLength;
    y[i] = yin - sin(angle) * segLength;
    segment(x[i], y[i], angle);
}

function segment(x, y, a) {
    push();
    translate(x, y);
    rotate(a);
    line(0, 0, segLength, 0);
    pop();
}

解説

これは、前のサンプルから基本的な機能はそのままで、ただ描く線分の長さを短くし、多数の線分の処理にforループを使っただけのサンプルです。しかしそれだけで、実際の動きの印象はずいぶん変わり、海蛇ように見えます。

「How can I move an object in an “infinity” or “figure 8” trajectory?」で見つけた次のコードを元に、８の字を描かせてみました(とは言え、これはインタラクションではありません)。

scale = 2 / (3 - cos(2 * t));
x = scale * cos(t);
y = scale * sin(2 * t) / 2;

ヘビゲーム

有名なヘビゲームです。ヘビの制御はi、j、k、lキーを使用します。ヘビが自分自身や壁に当たらないように気をつけて。Prashant Gupta作のサンプル。

// ヘビは小さなセグメントに分割され、draw()呼び出しのたびに描画され、編集される。
let numSegments = 10;
let direction = 'right';

const xStart = 0; // ヘビの開始のx座標
const yStart = 250; //  ヘビの開始のy座標
const diff = 10; // ヘビが1回に進む量

// ヘビのセグメントのxとy座標を保持する配列
let xCor = [];
let yCor = [];

// エサのxとy座標用
let xFruit = 0;
let yFruit = 0;
// スコアを表示するHTML要素
let scoreElem;

function setup() {
    // スコア表示用div要素を設定
    scoreElem = createDiv('スコア = 0');
    scoreElem.position(20, 20);
    scoreElem.id = 'score';
    scoreElem.style('color', 'white');

    createCanvas(500, 500);
    // このサンプルのフレームレート設定は速すぎるのでもっと遅くする
    // frameRate(15);
    frameRate(4);
    // セグメントは太い白線
    stroke(255);
    strokeWeight(10);
    // エサの位置を更新 初期値は(0,0)なので、ゲーム開始時に更新する
    updateFruitCoordinates();

    // xCorとyCor配列に値を入れる。
    for (let i = 0; i < numSegments; i++) {
        xCor.push(xStart + i * diff); // [0,10,20,...]
        yCor.push(yStart); // [250,250,250...]
    }
}

function draw() {
    background(0);
    for (let i = 0; i < numSegments - 1; i++) {
        // セグメントを描画
        line(xCor[i], yCor[i], xCor[i + 1], yCor[i + 1]);
    }
    // セグメントの座標、つまりxCorとyCorの要素の値を更新
    updateSnakeCoordinates();
    // ゲームオーバー状態にあるかどうかを調べる
    checkGameStatus();
    // エサを描画し、ヘビがエサを食べたかどうか調べる
    checkForFruit();
}

/*
 セグメントはヘビの方向(direction)にもとづいて更新される。
 0からn-1までの全セグメントは、１に、nまでコピーされる。
 つまり、セグメント0はセグメント1の値を得、セグメント1はセグメント2の値を得て、以降も同様に進む。
 これが、結果としてヘビの動きになる。

 最後のセグメントは、ヘビが進んでいる方向にもとづいて追加される。
 右に進んでいる場合には、最後のセグメントのx座標が、最後から２つめの値に定義済みの値diffを加えた値になり、
 左に進んでいる場合には、最後のセグメントのx座標が、最後から２つめの値からdiffを引いた値になる。
 上または下に進んでいる場合には、同様にして最後のセグメントのy座標が変更される。
*/
function updateSnakeCoordinates() {
    for (let i = 0; i < numSegments - 1; i++) {
        xCor[i] = xCor[i + 1];
        yCor[i] = yCor[i + 1];
    }
    switch (direction) {
        case 'right':
            xCor[numSegments - 1] = xCor[numSegments - 2] + diff;
            yCor[numSegments - 1] = yCor[numSegments - 2];
            break;
        case 'up':
            xCor[numSegments - 1] = xCor[numSegments - 2];
            yCor[numSegments - 1] = yCor[numSegments - 2] - diff;
            break;
        case 'left':
            xCor[numSegments - 1] = xCor[numSegments - 2] - diff;
            yCor[numSegments - 1] = yCor[numSegments - 2];
            break;
        case 'down':
            xCor[numSegments - 1] = xCor[numSegments - 2];
            yCor[numSegments - 1] = yCor[numSegments - 2] + diff;
            break;
    }
}

/*
 つねに、ヘビの頭の位置、つまりxCor[xCor.length - 1]とyCor[yCor.length - 1]が、
 ゲームの境界(キャンバスの上下左右の端)に触れているかどうか、
 またはヘビが自分自身に衝突しているかどうかを調べる
*/
function checkGameStatus() {
    if (
        // 頭がキャンバスの上下左右の端より外に出ているかどうか
        xCor[xCor.length - 1] > width ||
        xCor[xCor.length - 1] < 0 ||
        yCor[yCor.length - 1] > height ||
        yCor[yCor.length - 1] < 0 ||
        // またはヘビが自分の体と衝突しているかどうか
        checkSnakeCollision()
    ) {
        // 頭がキャンバスの外に出ているか、ヘビが自分に衝突していたら、
        // 描画を停止
        noLoop();
        // スコアを表示する
        const scoreVal = parseInt(scoreElem.html().substring(5));
        scoreElem.html('ゲームオーバー！ あなたのスコア： ' + scoreVal);
    }
}

/*
 ヘビが自分自身に衝突しているということは、
 ヘビの頭の(x,y)座標が、セグメントの(x,y)座標のどれか１つと同じだということ
*/
function checkSnakeCollision() {
    // 頭のx座標
    const snakeHeadX = xCor[xCor.length - 1];
    // 頭のy座標
    const snakeHeadY = yCor[yCor.length - 1];
    // xCor配列の長さ-1だけ繰り返す
    for (let i = 0; i < xCor.length - 1; i++) {
        // xCor配列のいずれかの値が、頭のx座標と等しくかつ頭のy座標と等しいなら、
        if (xCor[i] === snakeHeadX && yCor[i] === snakeHeadY) {
            // 衝突しているということなので、trueを返す
            return true;
        }
    }
}

/*
 ヘビがエサを食べたら、セグメントの数を１つ増やし、配列の先頭に、尾セグメントを挿入する。
 (尾に最後のセグメントを追加することで、尾を伸ばす)
*/
function checkForFruit() {
    // エサを描画
    point(xFruit, yFruit);
    // へびの頭のx座標とエサのx座標が等しく、かつへびの頭のy座標とエサのy座標が等しいなら => 食べた
    if (xCor[xCor.length - 1] === xFruit && yCor[yCor.length - 1] === yFruit) {
        // スコアを更新して表示
        const prevScore = parseInt(scoreElem.html().substring(5));
        scoreElem.html('スコア = ' + (prevScore + 1));
        // 配列の最初にxCor[0]の要素を追加
        xCor.unshift(xCor[0]);
        yCor.unshift(yCor[0]);
        // セグメント数を１つ増やす
        numSegments++;
        updateFruitCoordinates();
    }
}

// エサの位置を更新
function updateFruitCoordinates() {
    /*
      複雑な数学ロジックになっているのは、エサを100とwidth-100の間に置いて、
      ヘビは10の倍数で移動させるので、10で割り切れる最も近い数値に丸めるため。
    */

    xFruit = floor(random(10, (width - 100) / 10)) * 10;
    yFruit = floor(random(10, (height - 100) / 10)) * 10;
}

// keyPressed()はキーが押されたら1回だけ呼び出される。
function keyPressed() {
    switch (keyCode) {
        case 74:
            if (direction !== 'right') {
                direction = 'left';
            }
            break;
        case 76:
            if (direction !== 'left') {
                direction = 'right';
            }
            break;
        case 73:
            if (direction !== 'down') {
                direction = 'up';
            }
            break;
        case 75:
            if (direction !== 'up') {
                direction = 'down';
            }
            break;
    }
}

下の実行画面写真のクリックでサンプルが開きます。なおp5.jsサイトのサンプルはフレームレートが15に設定されていますが、ここではもっと遅くして、慣れないうちでもプレーしやすくしています。

解説

これは、1970年代に流行ったと言われる「Snake game(ヘビゲーム)」のp5.js版です。ウィキペディアには、次のように説明されています。

ヘビゲームは、ビデオゲームのジャンルのひとつ。伸長するヘビを操作して、エサを食べ続けることがゲームの目的である。

プレイヤーはヘビ（1キャラ分のブロックが連なり、細長い形状をしているもの）を操作し、その頭が画面の周囲あるいは自身の身体にぶつからないようにしながら、ランダムで出現するエサを回収する。エサを回収するたびにヘビの身体は1キャラずつ長くなっていく。ヘビは静止することができず、常に動き回っているため、エサを回収すればするほど自身の身体を回避することが難しくなる。

このp5.js版では、へびの向きを、キーボードのiキーの押し下げで上に、jキーの押し下げで左に、kキーで下に、lキーで右に変えます。これがこのサンプルのインタラクションです。

keyPressed()関数

keyPressed()は、キーが押されたときに１回だけ呼び出されます。キーが押しつづけられたときでも１回しか呼び出されないので、キーボードを使ったゲーム制作で重宝します。押されたキーのキーコードはkeyCode変数に保持されます。

p5.jsのキーの処理については「4_6：応答：キー p5.js JavaScript」で述べています。

配列を使ったセグメントの描画と座標の更新

ヘビの移動の動きは、xCorとyCor配列が保持するxとy座標にもとづいて描画された結果です。

draw()関数では、次のコードで、xCorとyCorの座標を使って線が描かれます。

// numSegments-1回だけ繰り返す
for (let i = 0; i < numSegments - 1; i++) {
    // xCorとyCorのi番めから、xCorとyCorのi番めの次までを結ぶ線を引く
    line(xCor[i], yCor[i], xCor[i + 1], yCor[i + 1]);
}

これは具体的に言うと、xCor[0]とyCor[0]と、１つ右のxCor[1]とyCor[1]を結ぶ線を描き、次にxCor[1]とyCor[1]と、１つ右のxCor[2]とyCor[2]を結ぶ線を描き、同様の同様の作業を配列の末尾までつづける、ということです。このときたとえばxCorに[0,10,20]、yCorに[250,250,250]という数値が入っていれば、(0,250)-(10,250)-(20,250)を結ぶ線が描かれます。

この１回のline()の呼び出しで描かれる線を、このサンプルではセグメントと呼んでいます。xCorとyCorの数値をインデックスを頼りに適切に変更すると、セグメントが描かれる場所が変わるので、結果としてへびが動いて見えるようになります。

xCorとyCorの数値を操作するのはupdateSnakeCoordinates()関数です。次のコードはこの関数の動作を探るためのもので、numSegmentsを3、xStartを250に変えています。またframeCount変数とnoLoop()関数を使って、適当な時間が経過したら描画を停めるようにしています。

// updateSnakeCoordinates()を探る

let numSegments = 3;
let direction = 'right';

const xStart = 250; // ヘビの開始のx座標
const yStart = 250; // ヘビの開始のy座標
const diff = 10;

// セグメントが取るx座標とy座標を入れる配列
let xCor = [];
let yCor = [];

function setup() {
    createCanvas(500, 500);
    frameRate(4);
    stroke(255);
    strokeWeight(10);

    // numSegments分だけ配列に数値を追加
    for (let i = 0; i < numSegments; i++) {
        xCor.push(xStart + i * diff);
        yCor.push(yStart);
    }
    print('初期値：xCor : ' + xCor); // [0,10,20]
    print('初期値：yCor : ' + yCor);
    print('------------------------------');
}

function draw() {
    background(0);
    // numSegments-1回だけ繰り返す
    for (let i = 0; i < numSegments - 1; i++) {
        // xCorとyCorのi番めから、xCorとyCorのi番めの次までを結ぶ線を引く
        line(xCor[i], yCor[i], xCor[i + 1], yCor[i + 1]);
    }
    // へびの座標を更新
    updateSnakeCoordinates();
    // 適当な時間が経過したら停める
    if (frameCount > 20) {
        noLoop()
    }
}

function updateSnakeCoordinates() {
    // xCorとyCorの要素を左に１つずらす。末尾の要素はそのまま残る
    print('処理対象xCor : ' + xCor); // [0,10,20]
    print('処理対象yCor : ' + yCor);
    for (let i = 0; i < numSegments - 1; i++) {
        xCor[i] = xCor[i + 1]; // 最初の[0,10,20]が、[10,20,20]=>[20,30,30]になる
        yCor[i] = yCor[i + 1]; //
    }
    print('左にシフトしたxCor : ' + xCor); // [10,20,20]
    print('左にシフトしたyCor : ' + yCor); // [10,20,20]
    // 変数directionの値に応じて処理を分ける
    switch (direction) {
        // 右：
        case 'right':
            //　xCorの末尾の要素の値を、末尾から1つ前の要素にdiffを足した値にする
            // xCorの末尾を、１つ前より10大きい値にする
            xCor[numSegments - 1] = xCor[numSegments - 2] + diff; // 最初の[10,20,20]が、[10,20,30]になる
            // yCorの末尾を、１つ前と同じ値にする
            yCor[numSegments - 1] = yCor[numSegments - 2];
            break;

        case 'up':
            // xCorの末尾を、１つ前と同じ値にする
            xCor[numSegments - 1] = xCor[numSegments - 2];
            //　yCorの末尾の要素の値を、末尾から1つ前の要素からdiffを引いた値にする
            yCor[numSegments - 1] = yCor[numSegments - 2] - diff;
            break;
        case 'left':
            //　xCorの末尾の要素の値を、末尾から1つ前の要素からdiffを引いた値にする
            // xCorの末尾を、１つ前より10小さい値にする
            xCor[numSegments - 1] = xCor[numSegments - 2] - diff;
            // yCorの末尾を、１つ前と同じ値にする
            yCor[numSegments - 1] = yCor[numSegments - 2];
            break;
        case 'down':
            // xCorの末尾を、１つ前と同じ値にする
            xCor[numSegments - 1] = xCor[numSegments - 2];
            //　yCorの末尾の要素の値を、末尾から1つ前の要素にdiffを足した値にする
            yCor[numSegments - 1] = yCor[numSegments - 2] + diff;
            break;

    }
    print('末尾を処理したxCor : ' + xCor); // [10,20,30]
    print('末尾を処理したyCor : ' + yCor); //
    print('------------------------------');
}

function keyPressed() {
    switch (keyCode) {
        case 74:
            if (direction !== 'right') {
                direction = 'left';
            }
            break;
        case 76:
            if (direction !== 'left') {
                direction = 'right';
            }
            break;
        case 73:
            if (direction !== 'down') {
                direction = 'up';
            }
            break;
        case 75:
            if (direction !== 'up') {
                direction = 'down';
            }
            break;
    }
    print(direction);
}

これを実行すると、下図に示すように、いくつかのタイミングでのxCorとyCorの値がコンソールに出力されます。numSegmentsを3にしているので、配列の要素数は3個です。

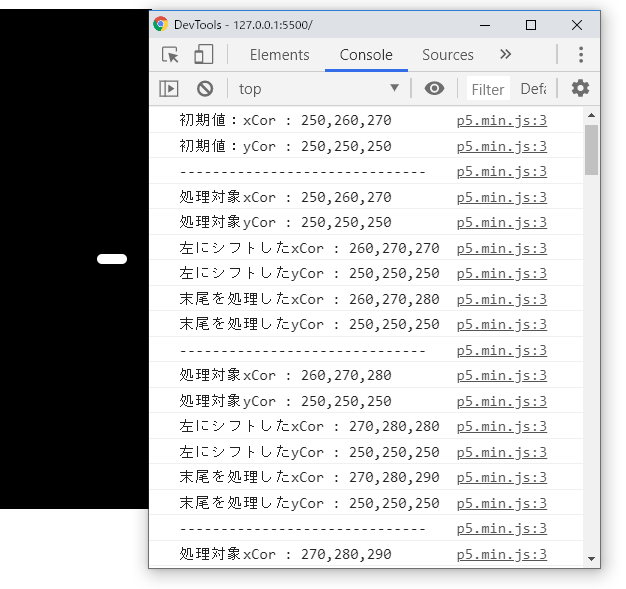
setup()関数ではxCorとyCorに座標の数値を入れています。diffは10なのでxCorは[0,10,20]になります。yCorは[250,250,250]です。

// numSegments分だけ配列に数値を追加
for (let i = 0; i < numSegments; i++) {
    xCor.push(xStart + i * diff);
    yCor.push(yStart);
}

draw()関数では、前述したforループ内のline()関数でxCorとyCorを使ってセグメントを描画し、その後updateSnakeCoordinates()関数を呼び出しています。これが調べたい関数です。

updateSnakeCoordinates()ではまず、次のforループで、配列の要素を１つ左にシフトしています。

// xCorとyCorの要素を左に１つずらす。末尾の要素はそのまま残る
for (let i = 0; i < numSegments - 1; i++) {
    xCor[i] = xCor[i + 1];
    yCor[i] = yCor[i + 1];
}

これは図で示すと、次のような作業です。配列の最初の要素は上書きされ、末尾の要素はそのまま残ります。具体的に言うと、[0,10,20]のxCorは[10,20,20]に、[250,250,250]のyCorは[250,250,250]になります。

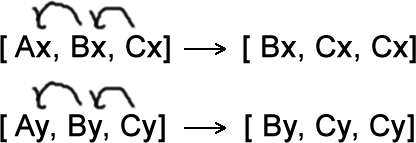
つづいてswitch (direction) {…があります。directionはヘビの進行方向を表す文字列で、初期値として’right’が指定されているので、次の３行が実行されます。

xCor[numSegments - 1] = xCor[numSegments - 2] + diff;
yCor[numSegments - 1] = yCor[numSegments - 2];
break;

これは、前のシフトでそのままになっていた末尾に対する操作で、xCorの末尾の数値を１つ前の数値より10大きい数値にし、yCorの末尾の数値を１つ前の数値と同じにして、caseステートメントを抜ける、という作業です。

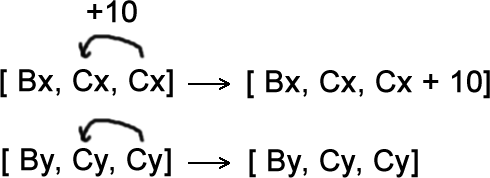
具体的に言うと、[10,20,20]のxCorは[10,20,30]に、[250,250,250]のyCorは[250,250,250]になります。updateSnakeCoordinates()関数の実行前、[0,10,20]だったxCorが[10,20,30]に変化したことになります。そして、これは’right’方向での操作なので、yCorは[250,250,250]のまま変化しません。

このxCorの変化によって、(0,250)->(10,250)への線は引かれなくなり、新たに(20,250)から(30,250)への線が引かれるようになります。これが描画されると、ヘビの右方向への移動に見えるわけです。同様の操作は、’left’、’up’、’down’の場合にも行われます。

波生成器

これは、決まった位置で振動するパーティクルから(海の波のような)波を生成する方法を示すサンプルです。マウスを動かすと波の方向が変わります。Dave Whyte作の「Orbiters」に着想を得た、Aatish Bhatiaによる投稿。

let t = 0; // 時間の変数

function setup() {
    createCanvas(600, 600);
    noStroke();
    fill(40, 200, 40);
}

function draw() {
    background(10, 10); // 半透明の背景(尾を作る)

    // 円のxとyグリッドを作成
    for (let x = 0; x <= width; x = x + 30) {
        for (let y = 0; y <= height; y = y + 30) {
            // 各円の開始位置はマウス位置によって変化する
            const xAngle = map(mouseX, 0, width, -4 * PI, 4 * PI, true);
            const yAngle = map(mouseY, 0, height, -4 * PI, 4 * PI, true);
            // また、パーティクルの位置にもとづいてもさまざまに変化する
            const angle = xAngle * (x / width) + yAngle * (y / height);

            // 各パーティクルは円の中を移動する
            const myX = x + 20 * cos(2 * PI * t + angle);
            const myY = y + 20 * sin(2 * PI * t + angle);

            ellipse(myX, myY, 10); // パーティクルを描画
        }
    }

    t = t + 0.01; // 時間を更新
}

下の実行画面写真のクリックでサンプルが開きます。

解説

このサンプルのインタラクションは、マウスの移動によって、パーティクルで作られる模様が変わる、ということです。特にマウスをキャンバスの４隅に移動させると、波が移動しているように見えます。このサンプルのコードは比較的短いものの、その中身は相当高度です。

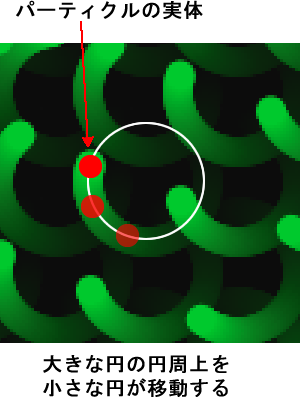
緑のパーティクルの尾

このサンプルでパーティクルと呼ばれているものの実体は、円の円周上を移動する、枠線なし、緑色の塗りで描画される円です。背景色に透明度が設定されているので、前のフレームが残存することになり、”尾”のように見えます。これは「９：シミュレーション 2/2 (Simulate)」の「ソフトボディ」で使われていたのと同様のテクニックです。

時間の組み込み

このサンプルでは、円の円周上を小さな円を移動させるテクニックが使用されていますが、これまでに何度も出てきた「7_6：円運動 p5.js JavaScript」の方法ではなく、時間の概念を組み込んだ方法で、小さな円のxとy位置を得ています。

時間の概念はdraw()関数の変数tで表されます。

let t = 0; // 時間の変数
function draw() {
    ...
    for(let x = 0; x <= width; x = x + 30) {
        for (let y = 0; y <= height; y = y + 30) {
            ...
            const myX = x + 20 * cos(2 * PI * t + angle);
            const myY = y + 20 * sin(2 * PI * t + angle);
            ...
        }
    }
    t = t + 0.01; // 時間を更新
}

tは0で初期化され、draw()が呼び出されるごとに0.01ずつ大きくなります。これは、draw()の1回の呼び出しで、0.01時間が経過する、という意味です。では、２重のforループの中の次の２行は、どのような考え方で点(myX, myY)を決めているのでしょう？

const myX = x + 20 * cos(2 * PI * t + angle);
const myY = y + 20 * sin(2 * PI * t + angle);

この２行は、「7_6：円運動 p5.js JavaScript」で見た次の２行と構成が同じです。したがって、変数xとyは円の中心座標(x, y)、20は円の半径と見なすことができます。

// (centerX, centerY)を中心とする半径がradiusの円
// 円周上のx座標値
const x = centerX + cosValue * radius;
// 円周上のy座標値
const y = centerY + sinValue * radius;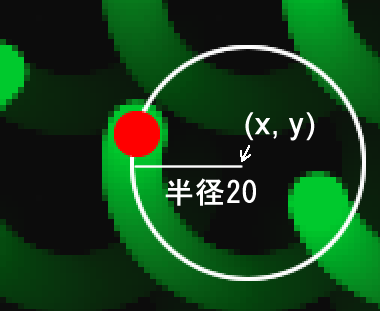

では2 * PI * tは何を意味しているのでしょう？　これは実は、角振動数(角周波数)と呼ばれるものを表しています。「波を表す6つ(+2)のパラメータ」ページによると、時間に関する波は、周期と振動数(周波数)、角振動数について、次の関係式が成り立ちます。

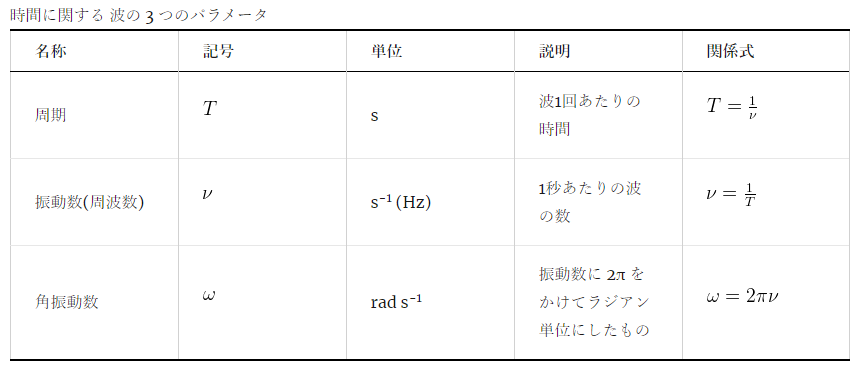
角振動数の式ω = 2πνは、ν = 1/Tなので、ω = 2π*1/Tとして使用できます。サンプルでtは0.01なので、0.01 = 1/T であり、するとTは100だと計算できます。 変数angleはひとまず無視して、時間のtとTを組み込んだ次のコードで、sin(TWO_PI * t)を使うとサイン波が描けます(2 * PIはp5.jsの定数TWO_PIで表せます)。

let t = 0;
const T = 100; // 周期

function setup() {
    print(1 / T); // 0.01 => サンプルで使われている数値
}

function draw() {
    // 角振動数(角周波数)　ω=2πν => 2π*1/T
    const y = sin(TWO_PI * t);
    t += 1 / T;

    plot(t, y);
    if (frameCount > T) {
        noLoop()
    }
}

下図は実行結果です。

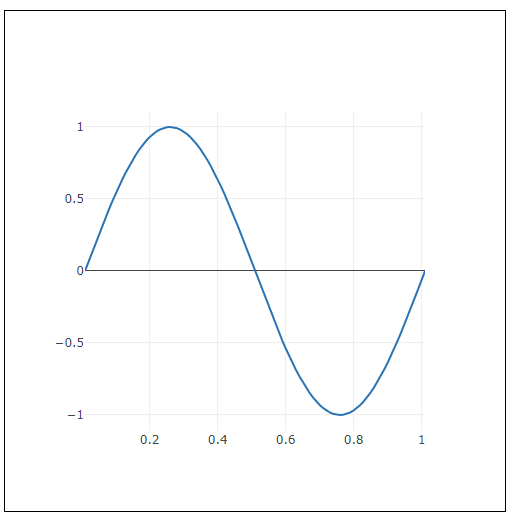
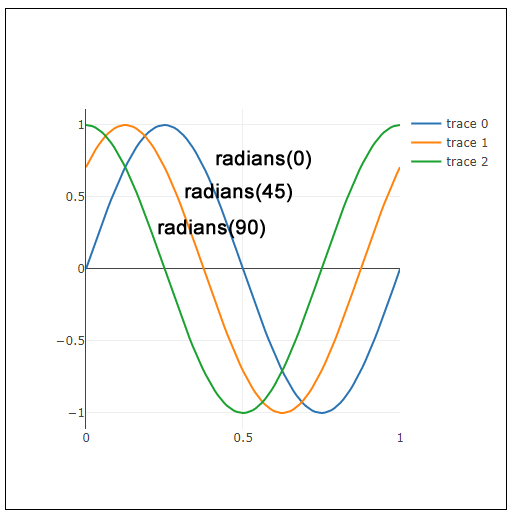
残ったのはangleです。これはサイン波を並べて描いたときのずれを生み出します。次のコードにように、sin(TWO_PI * t + angle)の変数angleに異なる角度を指定すると、angle分だけサイン波がずれます。

let t = 0;
const T = 100; // 周期

function setup() {
    print(1 / T); // 0.01 => サンプルで使われている数値
}

function draw() {


    let angle = radians(0);
    const y1 = sin(TWO_PI * t + angle);
    plot(t, y1);

    angle = radians(45);
    const y2 = sin(TWO_PI * t + angle);
    addPlot2(t, y2);

    angle = radians(90);
    const y3 = sin(TWO_PI * t + angle);
    addPlot3(t, y3);

    t += 1 / T;

    if (frameCount > T) {
        noLoop()
    }
}

円を２つ描く

ここまでで、サンプルの変数myXとmyYがどのような考え方で求められているかが分かったので、それを元に、次は実際に円を描いて動かしてみましょう。

次のコードは、サンプルの超簡易版です。サンプルでは変数xとyを0から30ずつ大きくしていますが、ここでは0と30に限っています。またxAngleとyAngleはマウス位置によって変化しますが、ここでは-720に固定しています。-720は、マウスがキャンバスの左上隅にあるときの値です。

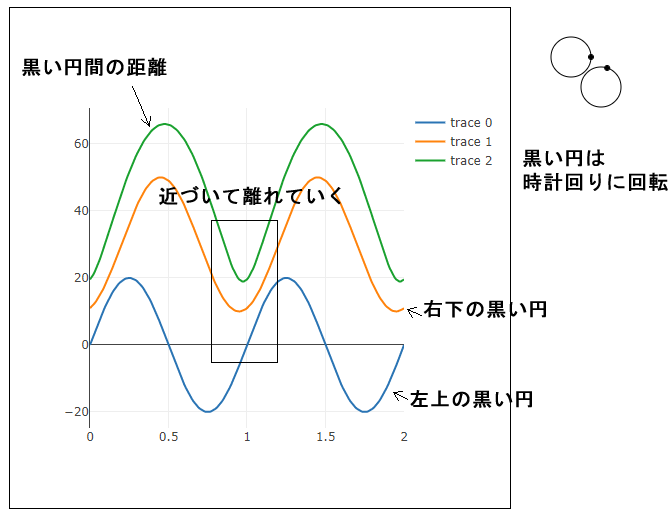
これを実行すると、キャンバスに大きな円が、キャンバスの左上から右下に向けて２つ描かれ、その円周上を小さな黒い円が移動します。また左には、t値を横軸、黒い円のy位置を縦軸にしたサイン波が２つと、２つの黒い円間の距離がグラフで描かれます。

const T = 100; // 周期
const radius = 20; // 円の半径

// 波のずれに影響する角度
let xAngle;
let yAngle;

let t = 0; // 時間

function setup() {
    const canvas = createCanvas(600, 600);
    canvas.parent('sketch-holder');
    stroke(0);
    // -720度を割り当てる
    xAngle = radians(-720);
    yAngle = radians(-720);
    // noLoop();
}


function draw() {
    background(255);
    // 描画を確認しやすいように移動
    translate(50, 50);

    // (x,y)を中心とする半径radiusの円を描画
    noFill();
    let x = 0;
    let y = 0;
    ellipse(x, y, radius * 2);

    // xAngleとx、width、yAngleとy、heightを要因にしてangleを作成
    // => xとyが0なので、angleは0
    let angle = xAngle * (x / width) + yAngle * (y / height); // 0
    print(degrees(angle));
    // 円周上のx座標値
    const x1 = x + radius * cos(TWO_PI * t + angle);
    // 円周上のy座標値
    const y1 = y + radius * sin(TWO_PI * t + angle);
    // 円周上を移動する小さな円を描く
    fill(0);
    ellipse(x1, y1, 5, 5);
    plot(t, y1);


    // 円をもう１つ右下に描く
    x = 30;
    y = 30;
    noFill();
    ellipse(x, y, radius * 2);
    angle = xAngle * (x / width) + yAngle * (y / height); // -72
    print(degrees(angle));
    const x2 = x + radius * cos(TWO_PI * t + angle);
    const y2 = y + radius * sin(TWO_PI * t + angle);
    fill(0);
    ellipse(x2, y2, 5, 5);
    addPlot2(t, y2);

    const distance = dist(x1, y1, x2, y2);
    addPlot3(t, distance);

    /*
    // 円をもう１つ右下に描く
    x = 60;
    y = 60;
    noFill();
    ellipse(x, y, radius * 2);
    angle = xAngle * (x / width) + yAngle * (y / height); // -144
    print(degrees(angle));
    const x3 = x + radius * cos(TWO_PI * t + angle);
    const y3 = y + radius * sin(TWO_PI * t + angle);
    fill(0);
    ellipse(x3, y3, 5, 5);
    addPlot4(t, y3);
    */
    t += 1 / T;
    // t += 0.01;

    if (frameCount > T * 2) {
        noLoop()
    }
}

黒い円は時計回りに大きな円の円周上を移動します。スタート位置がずれているので、円同士がニアミスして離れていくタイミングがあります。

また、３つめの円をx = 60、y = 60で描いて観察すると、１つめと２つめの円がニアミスして離れた後、２つめと３つめがニアミスして離れていくことが分かります(下図では距離のグラフは描いていません)。

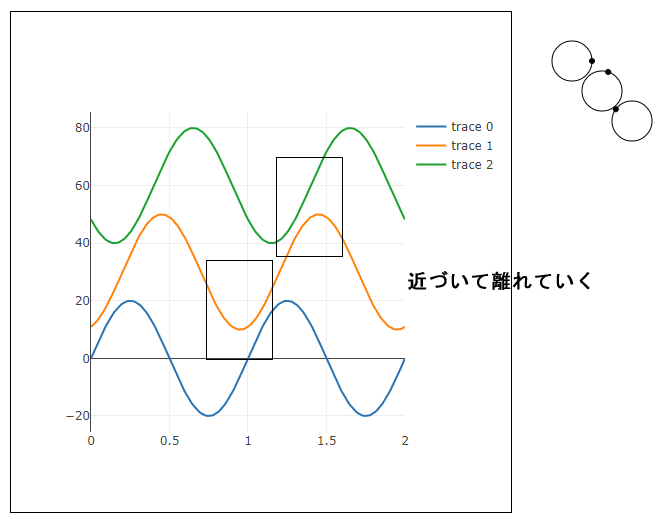
このニアミスして離れる動きが、右下方向に移動して見える波の元になります。

Dave WhyteのOrbitersを再現

ここまでが理解できたら、後は同じことを広げるだけです。サンプルの作者はDave WhyteのOrbitersに着想を得たそうなので、そのOrbitersを再現してみましょう。

let t = 0;
const radius = 20;

let xAngle;
let yAngle;;

let slider;
let sliderVal;

function setup() {
    createCanvas(600, 600);
    stroke(0);

    xAngle = radians(-720);
    yAngle = radians(-720);

    slider = setSlider();
    textSize(40);
    // noLoop();
}

function draw() {
    background(255);
    // スライダの値を調べて、ラジアン単位の角度に変換
    sliderVal = slider.value()
    xAngle = radians(sliderVal);
    yAngle = radians(sliderVal);

    // x => 0,30,60,90,...600
    for (let x = 0; x <= width; x = x + 30) {
        // y => 0,30,60,90,...600
        for (let y = 0; y <= height; y = y + 30) {
            // (x,y)を中心とする半径radiusの円を描画
            noFill();
            ellipse(x, y, radius * 2);

            // 波を打つポイントとなるコード
            // 0,-36,-72,-108,...(36度ずつ減る)
            const angle = xAngle * (x / width) + yAngle * (y / height);
            // print(degrees(angle));
            // angleだけずらす
            const myX = x + radius * cos(2 * PI * t + angle);
            const myY = y + radius * sin(2 * PI * t + angle);
            fill(0);
            // 円周上を移動する赤い円を描画
            ellipse(myX, myY, 5, 5);
        }
    }
    // スライダ値を左上に赤字で描画
    fill(255, 0, 0)
    text(sliderVal, 10, 50)

    t += 0.01;
}

// スライダを作成、設定して返す(要p5.dom.jsライブラリ)
function setSlider() {
    const slider = createSlider(-720, 720, -720, 30);
    slider.size(80, 30);
    slider.position(10, 610);
    slider.style('width', '600px');
    return slider;
}

下の実行画面写真のクリックでサンプルが開きます。キャンバス下にあるスライダを操作すると、xAngleとyAngleの値が変更できます。波は-720で左上から右下に進むように見え、値を上げていくとだんだんうねりが出てくるように感じます。0にするとサインとコサインの波のずれがなくなり完全に同期します。さらに大きくしていくと、今度は右下から左上に波が進むようになります。

リーチ１

アームは、atan2()を使った角度の計算によって、マウス位置に追随します。キース・ピータースのコードにもとづく。

const segLength = 80;
let x, y, x2, y2;

function setup() {
    createCanvas(710, 400);
    strokeWeight(20);
    stroke(255, 100);

    x = width / 2;
    y = height / 2;
    x2 = x;
    y2 = y;
}

function draw() {
    background(0);
    dragSegment();
}

function dragSegment() {
    background(0);

    const dx1 = mouseX - x;
    const dy1 = mouseY - y;
    const angle1 = atan2(dy1, dx1);

    const tx = mouseX - cos(angle1) * segLength;
    const ty = mouseY - sin(angle1) * segLength;

    const dx2 = tx - x2;
    const dy2 = ty - y2;
    const angle2 = atan2(dy2, dx2);
    x = x2 + cos(angle2) * segLength;
    y = y2 + sin(angle2) * segLength;

    segment(x, y, angle1);
    segment(x2, y2, angle2);
}

function segment(x, y, a) {
    push();
    translate(x, y);
    rotate(a);
    line(0, 0, segLength, 0);
    pop();
}

解説

”リーチ”とは、そこへ伸びる、といったニュアンスで、前の「ついて来る」と似ていますが、セグメント(線分)の根元が移動しません。上記サンプルはいささか丁寧さに欠け、変数名が具体的でなく分かりづらいので(恐らくは「リーチ２」以降で使用する配列を念頭に入れたものだと思われます)、以降では、具体的な変数名を使って、リーチの基本から見ていくことにします。

１つのセグメントのリーチ

次のコードは、１つのセグメントのリーチを表します。セグメントの根元(基点)はキャンバスセンターで、セグメントはマウスの方に向きます。しかし根本が固定されているので、自分の長さ以上には伸びません。

// １つのセグメント
const segLength = 80;
let baseX, baseY;

function setup() {
    createCanvas(710, 400);
    strokeWeight(20);
    stroke(255, 100);
    // 基点はキャンバスセンター
    baseX = width / 2;
    baseY = height / 2;
}

function draw() {
    background(0);
    reachSegment();
}

// セグメントの回転角度を計算して、基点を始点とするセグメントを描く
function reachSegment() {
        // baseからマウスへの角度を計算する
        const dx = mouseX - baseX;
        const dy = mouseY - baseY;
        // セグメントの回転角度
        const angle = atan2(dy, dx);

        // baseからマウス方向へのセグメントを描く
        segment(baseX, baseY, angle);
    }
    // (x, y)を原点としてa度だけ回転し、
    // その後原点である(x, y)から真右に向けて長さsegLengthの線を引く
function segment(x, y, a) {
    push();
    translate(x, y);
    rotate(a);
    line(0, 0, segLength, 0);
    pop();
}

１つのセグメントのリーチは簡単です。マウスの座標と基点の座標を使って、atan2()関数で角度を計算するだけです。

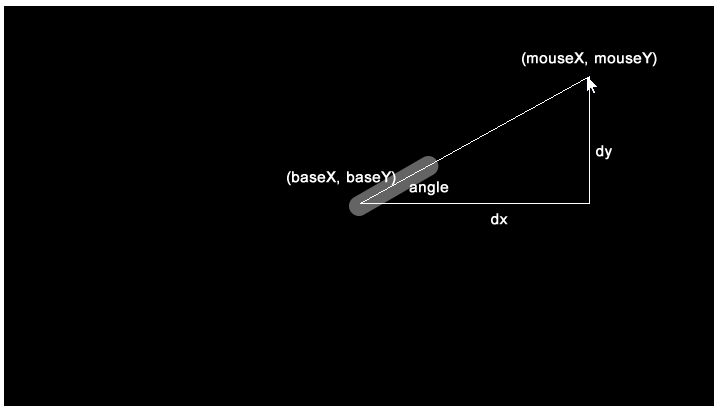
segment(x, y, a)関数は、与えられた(x, y)位置からaの角度で、長さsegLengthの線を描きます。xとyには線の描画を開始する座標を指定します。

２つのセグメントのリーチ

１つのセグメントのリーチは容易ですが、これが２つとなると難度が急に上がります。それは、下図に示す、アームの関節に当たる点(seg0X, seg0Y)を求める必要があるからです。

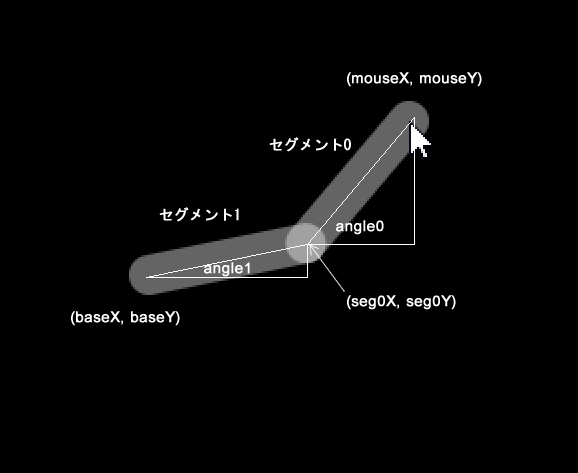
(seg0X, seg0Y)が分かると、(mouseX, mouseY)と合わせて使用してangle0が分かり、(baseX, baseY)と合わせて使用してangle1が分かります。すると、segment()関数に、seg0X, seg0Y, angle0を渡してセグメント0が、baseX, baseY,angle1を渡してセグメント1が描画できます。

そのコードは次のように記述できます。

// ２つのセグメント
const segLength = 80;
let baseX, baseY;
let target0X, target0Y; // セグメント0が向かう点のxとy座標
let seg0X, seg0Y; // セグメント0のxとy座標

function setup() {
    createCanvas(710, 400);

    baseX = width / 2;
    baseY = height / 2;

    target0X = 0;
    target0Y = 0;
    seg0X = 0; // 暫定的に指定
    seg0Y = 0; // 暫定的に指定
}

function draw() {
    background(0);
    reachSegment();

    // 参考用
    strokeWeight(1);
    stroke(255);
    noFill();
    // (mouseX,mouseY)を中心とする半径segLengthの円
    ellipse(mouseX, mouseY, segLength * 2);
    // (baseX,baseY)を中心とする半径segLengthの円
    ellipse(baseX, baseY, segLength * 2);
}

function reachSegment() {
    // セグメント0の角度を求める
    // (mouseX, mouseY)と(seg0X,seg0Y)から角度を計算する
    const dx0 = mouseX - seg0X;
    const dy0 = mouseY - seg0Y;
    const angle0 = atan2(dy0, dx0);

    // angle0が分かると、(mouseX, mouseY)を中心とする半径segLengthの円周上の点が計算できる
    target0X = mouseX - cos(angle0) * segLength;
    target0Y = mouseY - sin(angle0) * segLength;
    // この点を赤い円で描く
    fill(255, 0, 0);
    noStroke();
    ellipse(target0X, target0Y, 20);

    // セグメント1の角度を求める
    // (targetX0,targetY0)と(baseX, baseY)から角度を計算する
    const dx1 = target0X - baseX;
    const dy1 = target0Y - baseY;
    const angle1 = atan2(dy1, dx1);

    // セグメントの開始位置(baseX, baseY)は分かっており、角度が分かったので、
    // (baseX, baseY)を中心とする半径segLengthの円周上の点が計算できる。
    // seg0Xとseg0Yに正しい値を代入する(0でスタートしているので)
    seg0X = baseX + cos(angle1) * segLength;
    seg0Y = baseY + sin(angle1) * segLength;
    // この点を黄色の円で描く
    fill(255, 255, 0);
    ellipse(seg0X, seg0Y, 20);

    // セグメント0を描く
    segment(seg0X, seg0Y, angle0);
    // セグメント1を描く
    segment(baseX, baseY, angle1);
}

// xとyは始点、aは回転する角度
function segment(x, y, a) {
    push();
    translate(x, y);
    rotate(a);
    strokeWeight(20);
    stroke(255, 100);
    line(0, 0, segLength, 0);
    strokeWeight(1);
    pop();
}

次の実行画面では、赤い円が点(targetX0,targetY0)を、黄色い円が点(seg0X,seg0Y)の位置を示しています。

ただしこのプログラムには、巧妙なトリックまたは嘘が含まれています。次のコードはreachSegment()関数のコードです。冒頭でmouseXからseg0Xを引き、mouseYからseg0Yを引いています。その後計算が進み、終わりの方で、seg0Xとseg0Yに、 (baseX, baseY)を中心とする半径segLengthの円周上の点を代入しています。

// セグメント0の角度を求める 
const dx0 = mouseX - seg0X;
const dy0 = mouseY - seg0Y;
const angle0 = atan2(dy0, dx0);

// (mouseX, mouseY)を中心とする半径segLengthの円周上の点
target0X = mouseX - cos(angle0) * segLength;
target0Y = mouseY - sin(angle0) * segLength;

// その点を使ってセグメント1の角度を求める
const dx1 = target0X - baseX;
const dy1 = target0Y - baseY;
const angle1 = atan2(dy1, dx1);

// (baseX, baseY)を中心とする半径segLengthの円周上の点
seg0X = baseX + cos(angle1) * segLength;
seg0Y = baseY + sin(angle1) * segLength;

// セグメント0と1を描く
segment(seg0X, seg0Y, angle0);
// セグメント1を描く
segment(baseX, baseY, angle1);

一見問題はなさそうに思えますが、実はreachSegment()関数が初めて呼び出されるとき、seg0Xとseg0Yは暫定値の0なので、以降の計算は正しいものではありません。終わりのeg0Xとseg0Yへの円周上の点の代入で初めて、eg0Xとseg0Yには適切な値が入ります。つまり、このプログラムはdraw()の1回めの呼び出しだけでは適切に動作しないプログラムなのです。とは言えそれは一瞬のことで、draw()の２回めの呼び出し以降では正しく動作するので、実際には問題は発生しません。

リーチ２

アームは、atan2()を使った角度の計算によって、マウス位置に追随します。キース・ピータースのコードにもとづく。

let numSegments = 10,
    x = [],
    y = [],
    angle = [],
    segLength = 26,
    targetX,
    targetY;

for (let i = 0; i < numSegments; i++) {
    x[i] = 0;
    y[i] = 0;
    angle[i] = 0;
}

function setup() {
    createCanvas(710, 400);
    strokeWeight(20);
    stroke(255, 100);

    x[x.length - 1] = width / 2; // 基点のx座標
    y[x.length - 1] = height; // 基点のy座標
}

function draw() {
    background(0);

    reachSegment(0, mouseX, mouseY);
    for (let i = 1; i < numSegments; i++) {
        reachSegment(i, targetX, targetY);
    }
    for (let j = x.length - 1; j >= 1; j--) {
        positionSegment(j, j - 1);
    }
    for (let k = 0; k < x.length; k++) {
        // (k + 1) * 2 => 繰り返しが進むほど大きな値になる
        segment(x[k], y[k], angle[k], (k + 1) * 2);
    }
}

function positionSegment(a, b) {
    x[b] = x[a] + cos(angle[a]) * segLength;
    y[b] = y[a] + sin(angle[a]) * segLength;
}

function reachSegment(i, xin, yin) {
    const dx = xin - x[i];
    const dy = yin - y[i];
    angle[i] = atan2(dy, dx);
    targetX = xin - cos(angle[i]) * segLength;
    targetY = yin - sin(angle[i]) * segLength;
}

// swは線の太さ
function segment(x, y, a, sw) {
    // 線はだんだん太くなる => セグメント0よりセグメント1の方が太くなる
    strokeWeight(sw);
    push();
    translate(x, y);
    rotate(a);
    line(0, 0, segLength, 0);
    pop();
}

解説

前の「２つのセグメントのリーチ」と見た目がずいぶん変わっていますが、考え方は「２つのセグメントのリーチ」で示した図と同じです。

変わっているのは、複数個のセグメントが可変的に扱えるように関数化し、セグメントの描画開始位置であるxとyと角度のangleを配列にしたことです。セグメントの個数は変数numSegmentsに指定します。

とは言え、新しいreachSegment(i, xin, yin)関数やpositionSegment(a, b)関数の理解は決してやさしくはないので、次の「２つのセグメントのリーチ」と同じ形状をした３つのセグメントで、サンプルコードの中身を見ていきます。

const numSegments = 3;
const segLength = 80;

// セグメントのxとy座標、回転角度を入れる配列
let x = [],
    y = [],
    angle = [];
// 次のセグメントが向かう(x, y)座標
let targetX, targetY;

// xとy、angle配列をnumSegments個の0で埋める
for (let i = 0; i < numSegments; i++) {
    x[i] = 0;
    y[i] = 0;
    angle[i] = 0;
}

function setup() {
    createCanvas(710, 400);
    strokeWeight(20);
    stroke(255, 100);
    // xとy配列の末尾要素の値を幅の半分と高さにする
    x[x.length - 1] = width / 2; // 基点のx座標 [0,0,355]
    y[x.length - 1] = height / 2; // 基点のy座標 [0,0,200]
}

function draw() {
    background(0);

    // マウス位置に一番近いセグメント0について角度を計算し、
    // 変数targetXとtargetYに正しい値を割り当てる
    reachSegment(0, mouseX, mouseY);

    // セグメント1以降について角度を求め、
    // 次のセグメント用のtargetXとtargetYを計算しておく
    for (let i = 1; i < numSegments; i++) {
        reachSegment(i, targetX, targetY);
    }

    // 配列には、[セグ0、セグ1、セグ2]の順でxとy座標、角度の値が入っている。

    // 配列を末尾からループ(逆順)
    // https://infoteck-life.com/a0121-js-array-loop-reverse/
    for (let j = x.length - 1; j >= 1; j--) {
        // 当該インデックスと、その１つ左のインデックスを渡す
        // セグ2とセグ1、セグ1とセグ0というように。
        // 先頭のセグ0には処理は不要(j >= 1)だが、処理しても問題にはならない(j >= 0)
        positionSegment(j, j - 1);
    }

    // セグメントkを描く
    for (let k = 0; k < x.length; k++) {
        segment(x[k], y[k], angle[k]);
    }
}

// セグメントiの角度を計算してangle配列に入れ、
// (xin, yin)を中心とする半径segLengthの円周上の点(targetX, targetY)を求める
function reachSegment(i, xin, yin) {
    const dx = xin - x[i];
    const dy = yin - y[i];
    angle[i] = atan2(dy, dx);
    // 次のターゲット(向く先)になる
    targetX = xin - cos(angle[i]) * segLength;
    targetY = yin - sin(angle[i]) * segLength;
    // 参考用
    fill(255, 0, 0);
    ellipse(targetX, targetY, 20, 20);
}

// 当該インデックス(a)と、その１つ左のインデックス(b)を使って、
// 左のインデックスに相当するセグメントの(x,y)位置を決める
// ex:セル0とセル1
function positionSegment(a, b) {
    // 当該インデックスの(x[a],y[a])を中心とする半径segLengthの円周上の点を、
    // 当該インデックスの１つ左のインデックスの値にする。
    // 配列の末尾は扱わないので、末尾の値は変わらず、355,200のまま
    x[b] = x[a] + cos(angle[a]) * segLength;
    y[b] = y[a] + sin(angle[a]) * segLength;
    // 参考用。セグメントの(x,y)位置を黄色の円で描く
    //print(x[b], y[b]);
    fill(255, 255, 0);
    ellipse(x[b], y[b], 20, 20);
}


function segment(x, y, a) {
    strokeWeight(20);
    push();
    translate(x, y);
    rotate(a);
    line(0, 0, segLength, 0);
    pop();
    strokeWeight(1);

}

プログラムがsetup()関数まで進むと、配列xは[0,0,355]、yは[0,0,200]、angleは[0,0,0]になります。xとyの末尾を組み合わせると(355, 200)になり、根元のセグメントの描画開始位置に当たります。マウスに一番近いものをセグメント0とすると、xとy、angleの要素は[セグメント0, セグメント1, セグメント2]の順に並んでいると考えられます。

draw()関数では、background(0)の後、reachSegment(0, mouseX, mouseY)を呼び出しています。これはマウスに一番近いセグメント(つまりセグメント0)の角度と、次のセグメントのために正しいtargetXとtargetYを計算します(一番最初の呼び出し時にはundefinedです)。

// セグメントiの角度を計算してangle配列に入れ、
// (xin, yin)を中心とする半径segLengthの円周上の点(targetX, targetY)を求める
function reachSegment(i, xin, yin) {
    const dx = xin - x[i];
    const dy = yin - y[i];
    angle[i] = atan2(dy, dx);
    // 次のターゲット(向く先)になる
    targetX = xin - cos(angle[i]) * segLength;
    targetY = yin - sin(angle[i]) * segLength;
    // 参考用
    fill(255, 0, 0);
    ellipse(targetX, targetY, 20, 20);
}

その後のforループでは、セグメント1と2について、正確なtargetXとtargetYを使って、角度を計算します。角度の数値は配列angleにセグメント0、セグメント1、セグメント2の順に入ります。

for (let i = 1; i < numSegments; i++) {
    reachSegment(i, targetX, targetY);
}

これで３つのセグメントの角度が計算できangle配列に入りました。次はセグメントの描画を開始する位置(segment()関数に渡すxとy)を求めます。

for (let j = x.length - 1; j >= 1; j--) {
    positionSegment(j, j - 1);
}
...
function positionSegment(a, b) {
    x[b] = x[a] + cos(angle[a]) * segLength;
    y[b] = y[a] + sin(angle[a]) * segLength;
}

コード自体は短いのでやさしそうに見えます。forループで行っているのは、配列の末尾からのループ処理です。書き方が変則的なだけで、やっていることは簡単です(「配列を逆順にループする方法」)。

positionSegment()関数は、受け取ったaとbをxとyのいんでとして使用し、点(x[a], y[a])を中心とする半径segLengthの円周上の点をxとy配列の[b]番めの要素として割り当てています。これもさほど難しいコードではありません。

何をやっているかは理解できますが、なぜこうしているのかを理解するのはなかなか難しいと思われるので、ここでも具体的に見ていきましょう。

今この段階で分かっているのは、根元の位置と３つのセグメントの角度です。根元の位置はx[2]とy[2]にあり、角度はangle配列に[セグメント0、セグメント1、セグメント2]の順に入っています。

まずセグメント2は、描画開始位置と角度が分かっているので、segment()にこれらを渡すことで描画できます。

// セグメント2は描画できる
segment(x[2], y[2], angle[2]);

次に計算できそうなのは、セグメント1の描画開始位置です。これは、(x[2], y[2])を中心とする半径segLengthの円周上の点です。

x[1] = x[2] + cos(angle[2]) * segLength;
y[1] = y[2] + sin(angle[2]) * segLength;
segment(x[1], y[1], angle[1]);

セグメント1の描画開始位置が分かったら、同様にしてセグメント0の描画開始位置も計算できます。

 x[0] = x[1] + cos(angle[1]) * segLength;
 y[0] = y[1] + sin(angle[1]) * segLength;
 segment(x[0], y[0], angle[0]);

これだけのこと(segment()関数への呼び出しをのぞく)を一気にやろうとするのが、前述したforループとpositionSegment()関数なのです。今の場合にはセグメント数が３つなので、１つずつ計算してもさほどの手数ではありませんが、サンプルのように10個もあると、関数でまとめて処理した方が効率的です。

リーチ３

アームは、atan2()を使った角度の計算によって、マウス位置に追随します。キース・ピータースのコードにもとづく。

let numSegments = 8,
    x = [],
    y = [],
    angle = [],
    segLength = 26,
    targetX,
    targetY,
    ballX = 50,
    ballY = 50,
    ballXDirection = 1,
    ballYDirection = -1;

for (let i = 0; i < numSegments; i++) {
    x[i] = 0;
    y[i] = 0;
    angle[i] = 0;
}

function setup() {
    createCanvas(710, 400);
    strokeWeight(20);
    stroke(255, 100);
    noFill();

    x[x.length - 1] = width / 2;
    y[x.length - 1] = height;
}

function draw() {
    background(0);

    strokeWeight(20);
    ballX = ballX + 1.0 * ballXDirection;
    ballY = ballY + 0.8 * ballYDirection;
    // ボールの左右の壁に対する跳ね返り
    if (ballX > width - 25 || ballX < 25) {
        ballXDirection *= -1;
    }
    // ボールの上下の壁に対する跳ね返り
    if (ballY > height - 25 || ballY < 25) {
        ballYDirection *= -1;
    }
    ellipse(ballX, ballY, 30, 30);

    reachSegment(0, ballX, ballY);
    for (let i = 1; i < numSegments; i++) {
        reachSegment(i, targetX, targetY);
    }
    for (let j = x.length - 1; j >= 1; j--) {
        positionSegment(j, j - 1);
    }
    for (let k = 0; k < x.length; k++) {
        segment(x[k], y[k], angle[k], (k + 1) * 2);
    }
}

function positionSegment(a, b) {
    x[b] = x[a] + cos(angle[a]) * segLength;
    y[b] = y[a] + sin(angle[a]) * segLength;
}

function reachSegment(i, xin, yin) {
    const dx = xin - x[i];
    const dy = yin - y[i];
    angle[i] = atan2(dy, dx);
    targetX = xin - cos(angle[i]) * segLength;
    targetY = yin - sin(angle[i]) * segLength;
}

function segment(x, y, a, sw) {
    strokeWeight(sw);
    push();
    translate(x, y);
    rotate(a);
    line(0, 0, segLength, 0);
    pop();
}

解説

これは前の「リーチ２」の応用で、マウスの代わりに、キャンバス内を跳ね返って移動するボールにリーチします。ボールにリーチさせるには、draw()関数で、reachSegment(0, mouseX, mouseY)のmouseXとmouseYを、ballXとballYに置き換えるだけです。

これはreachSegment()関数とこのプログラムの柔軟性をよく示しています。柔軟性を備えたプログラムは良いプログラムだと言えます。