16：入力(Input)

時計

現在の時刻は、second()やminute()、hour()関数で読み取ることができます。このサンプルでは、 sin()とcos()値を使って、時計の針の位置を設定しています。

let cx, cy; // 時計の中心
let secondsRadius; // 秒針用の半径
let minutesRadius; // 分針用の半径
let hoursRadius; // 時針用の半径
let clockDiameter; // 時計の直径

function setup() {
    createCanvas(720, 400);
    stroke(255);

    let radius = min(width, height) / 2; // 幅と高さの小さい方(高さ)の半分(=200)を基準に以下を決める
    secondsRadius = radius * 0.71; // 秒針用の半径
    minutesRadius = radius * 0.6; // 分針用の半径
    hoursRadius = radius * 0.5; // 時針用の半径
    clockDiameter = radius * 1.7; // 時計の直径

    cx = width / 2; // 中心のx座標
    cy = height / 2; // 中心のy座標
}

function draw() {
    background(230);

    // 時計の背景を描く
    noStroke();
    fill(244, 122, 158);
    ellipse(cx, cy, clockDiameter + 25, clockDiameter + 25);
    fill(237, 34, 93);
    ellipse(cx, cy, clockDiameter, clockDiameter);

    // sin()とcos()の角度は3時(=0度)から始まるので、
    // 0時(-90度)から始まるようにHALF_PI(90度)を引く
    let s = map(second(), 0, 60, 0, TWO_PI) - HALF_PI;
    let m = map(minute() + norm(second(), 0, 60), 0, 60, 0, TWO_PI) - HALF_PI;
    let h = map(hour() + norm(minute(), 0, 60), 0, 24, 0, TWO_PI * 2) - HALF_PI;

    // 時計の針を描く
    stroke(255);
    strokeWeight(1);
    line(cx, cy, cx + cos(s) * secondsRadius, cy + sin(s) * secondsRadius);
    strokeWeight(2);
    line(cx, cy, cx + cos(m) * minutesRadius, cy + sin(m) * minutesRadius);
    strokeWeight(4);
    line(cx, cy, cx + cos(h) * hoursRadius, cy + sin(h) * hoursRadius);

    // インデックス(分刻みの点)を描く
    strokeWeight(2);
    beginShape(POINTS);
    for (let a = 0; a < 360; a += 6) {
        let angle = radians(a);
        let x = cx + cos(angle) * secondsRadius;
        let y = cy + sin(angle) * secondsRadius;
        vertex(x, y);
    }
    endShape();
}

解説

このサンプルの入力は、コンピュータが持っている時刻情報です。p5.jsはこれを、year()、month()、day()、hour()、minute()、second()関数で取得できます。

// 2019年12月9日 8時51分48秒
print(year()); // 2019
print(month()); // 12
print(day()); // 9
print(hour()); // 8
print(minute()); // 51
print(second()); // 48

時刻を角度に

時刻の数値、たとえば3時なら3、56分なら56を、アナログ時計の針で示すには、その数値をアナログ時計での針の角度に直す必要があります。また、分針や時針を滑らかに動かしたい場合、つまり2分から3分に変わるとき、いきなり角度が変わるのではなく、2分と3分の間も針が指すようにしたい場合には、60秒未満の秒数も分数換算して加える必要があります。

通常のJavaScriptでアナログ時計を作るときには、setInterval()関数を使った次のようなコードがよく使用されます。しかしp5.jsのdraw()関数はデフォルトで１秒間に60回呼び出されるので、draw()内での使用は適当ではありません。

// 1秒に1回、{ }内の関数を実行
window.setInterval(() => {
    // 現在時刻を取得
    const date = new Date();
    // 秒：(360 / 60)は1秒当たりに進めばよい角度。これに今の秒数を掛ける。
    const s = date.getSeconds() * (360 / 60);
    // 分：分には、まだ1分に満たない秒数を、分数に換算して加える
    const m = date.getSeconds() * (360 / 60) + (s / 60);
    // 時：時には、まだ1時間に満たない分数を、時数に換算して加える
    const h = date.getHours() * (360 / 24) + (m / 24);
}, 1000);

このサンプルでは、p5.jsお得意のmap()関数と数値の正規化を行うnorm()関数の併用で秒数と分数の換算を行い、sin()とcos()関数を使って針を動かす、というスマートな方法が取られています。作業はdraw()内で行われるので、針のアニメーションは滑らかに表示されます。

秒針を描く

次のコードは、second()関数から今の秒数を取得して、秒針を描く例です。

let cx, cy; // 時計の中心
let secondsRadius;

function setup() {
    createCanvas(720, 400);
    textSize(30);
    fill(255)
    stroke(255);

    let radius = min(width, height) / 2; // 幅と高さの小さい方(高さ)の半分(=200)を基準に以下を決める
    secondsRadius = radius * 0.71; // 秒針用の半径
    cx = width / 2; // 中心のx座標
    cy = height / 2; // 中心のy座標
}

// 今の秒数を、秒針で表す
function draw() {
    background(0);

    fill(255);
    // 今の秒数を取得し描画
    const seconds = second();
    text(seconds, 20, 50);

    // 今の秒数を、0-360度に対応付け
    const sec = map(seconds, 0, 60, 0, TWO_PI);
    // 今の秒数は何ラジアン度か => 分かりやすいように度数に変換
    text(degrees(sec), 20, 100);
    // そこから90度引く => => 分かりやすいように度数に変換
    const s = sec - HALF_PI;
    text(degrees(s), 20, 150);

    // 時計の針を描く
    stroke(255);
    strokeWeight(1);

    // 点(cx,cy)を中心とする半径secondsRadiusの円の円周上の点
    const xpos = cx + cos(s) * secondsRadius;
    const ypos = cy + sin(s) * secondsRadius;
    // 秒針を線で描く
    line(cx, cy, xpos, ypos);

    noFill();
    // 点(cx,cy)を中心とする半径secondsRadiusの円
    ellipse(cx, cy, secondsRadius * 2);
    // そこに小さな赤い円を描く => 秒針の線の終端
    fill(255, 0, 0);
    ellipse(xpos, ypos, 10, 10);
}

キャンバスの左上には、second()関数で得た今の秒数と、その秒数を指す針の角度(計算に使うのはラジアン値ですが、分かりやすいように度数に変換しています)、そこから90度引いた角度を文字で描画しています。

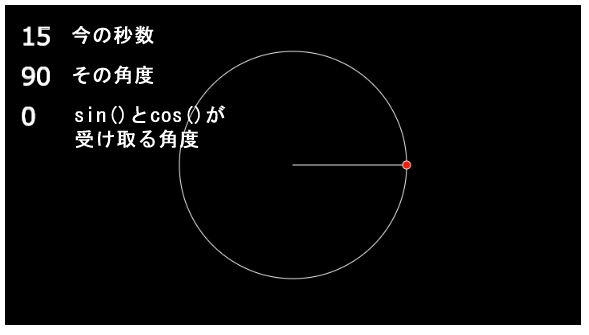
この３つの数値の表示は、次の６行で行っています。

今の秒数を調べ、それを描画しているのは初めの２行です。変数secondsには秒数の数値が代入され、text()関数によってそれが描画されます。
その下では、この0と60の間の数値が、0度から360度(TWO_PI)では何度に相当するかをmap()関数で計算しています。map()関数については「4_7：マッピング(対応付け) p5.js JavaScript」で述べています。

その下の行では、その角度に当たる数値を、前の秒数の下に描画し、終わりの２行では、秒数の角度から90度を引いてそれを描画しています。上図の例では、秒数が15なので、時計の15秒を指す角度の90度と、そこから90度を引いた0が表示されています。

const seconds = second();
text(seconds, 20, 50);
const sec = map(seconds, 0, 60, 0, TWO_PI);
text(degrees(sec), 20, 100);
const s = sec - HALF_PI;
text(degrees(s), 20, 150);

秒数の角度から90度を引くのは、角度をsin()とcos()関数で使用するためです。sin()とcos()の0度は時計の中心から真右の角度ですが、時計の0秒は真上なので、この違いを吸収するために90を引いています。

その下のコードでは、cos()とsin()関数に90度引いた角度を渡し、xposとyposの数値を得ています。この２行は、点(cx,cy)を中心とする半径secondsRadiusの円の円周上の点を計算するコードです。点(cx,cy)から見て角度sの点は(xpos, ypos)なので、この２点を線で結ぶと、現在の秒数を指す秒針になります。

const xpos = cx + cos(s) * secondsRadius;
const ypos = cy + sin(s) * secondsRadius;
line(cx, cy, xpos, ypos);

// 参考用
noFill();
ellipse(cx, cy, secondsRadius * 2);
fill(255, 0, 0);
ellipse(xpos, ypos, 10, 10);

分針を描く

次のコードは、前の秒針につづいて、分針も描画するコードです。また１分刻みの目盛りも描いています。

let cx, cy;
let secondsRadius;
let minutesRadius;

function setup() {
    createCanvas(720, 400);
    textSize(30);
    fill(255)
    stroke(255);

    let radius = min(width, height) / 2; // 幅と高さの小さい方(高さ)の半分(=200)を基準に以下を決める
    secondsRadius = radius * 0.71; // 秒針用の半径
    minutesRadius = radius * 0.6; // 分針用の半径

    cx = width / 2; // 中心のx座標
    cy = height / 2; // 中心のy座標
}

function draw() {
    background(0);

    fill(255);
    let s = map(second(), 0, 60, 0, TWO_PI) - HALF_PI;
    // 今の秒数は分に直すと何分か
    const normalizedValue = norm(second(), 0, 60);
    text(normalizedValue, 20, 50);
    // 秒数も含む今の分数
    const minutePlus = minute() + normalizedValue;
    text(minutePlus, 20, 100);
    // 今の分数を、0-360度に対応付けて、そこから90度引く
    const m = map(minutePlus, 0, 60, 0, TWO_PI) - HALF_PI;

    // 時計の針を描く
    stroke(255);
    strokeWeight(1);
    line(cx, cy, cx + cos(s) * secondsRadius, cy + sin(s) * secondsRadius);

    // 秒針より太くして、分針を描く
    strokeWeight(2);
    line(cx, cy, cx + cos(m) * minutesRadius, cy + sin(m) * minutesRadius);

    // 分刻みの点を描く
    strokeWeight(2);
    beginShape(POINTS);
    // 1時間は60分
    // 1時間:60分 = 360度:6度　なので6刻み
    for (let a = 0; a < 360; a += 6) {
        let angle = radians(a);
        let x = cx + cos(angle) * secondsRadius;
        let y = cy + sin(angle) * secondsRadius;
        vertex(x, y);
    }
    endShape();
}

このコードでも、キャンバス左に数値を描画しています。上は今の秒数を分数に直すと何秒かを示す数値です。60秒未満の秒数を換算するので1未満になります。その下はこの換算した分数と今の秒数を足した分数です。下図では0.4分なので、今の分数は49.4分(つまり49分24秒)となります。この値を角度に使用することで、分針が49分と50分の間を指すようになります。

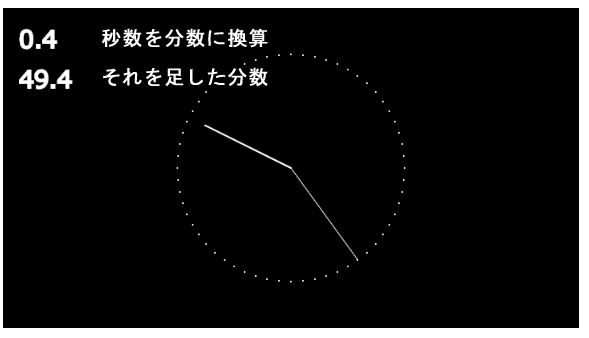
この計算は面倒に思えますが、p5.jsのnorm()関数を使うと、容易に行えます。実際、サンプルではmap()とnorm()を組み合わせるて、1行で計算を終えています。

const normalizedValue = norm(second(), 0, 60);
const minutePlus = minute() + normalizedValue;
const m = map(minutePlus, 0, 60, 0, TWO_PI) - HALF_PI;

norm()関数は、その名前通り、与えられた数値と範囲を使って、その数値を1と0の間に正規化します。上記の場合には、second()が返す秒数を、0と60の間の数値に置き換えます。24秒なら、24/60=0.4 となるわけです。これは言わば半端な分数で、minute()から得られる今の分数に足します。後は、秒針のときと同じように、角度に置き換えて90度を引きます。

分刻みの目盛りは、0から360未満までを6刻みで繰り返すforループで、円の円周上の点を求めるのと同じ要領で描画できます。なお、beginShape()に渡している定数POINTSは、作成した頂点で点を描画することを意味するオプションです。

beginShape(POINTS);
// 1時間は60分
// 60分:1分 = 360度:x　なので6刻み
for (let a = 0; a < 360; a += 6) {
    let angle = radians(a);
    let x = cx + cos(angle) * secondsRadius;
    let y = cy + sin(angle) * secondsRadius;
    vertex(x, y);
}
endShape();

リファレンスメモ

norm()

説明

範囲が別の数値を、0と1の間の値に正規化する。これはmap(value, low, high, 0, 1)と同じ。範囲外の数値は意味があり有用な場合が多いので、0と1の間に固定されない。

シンタックス

norm(value, start, stop)

パラメータ

value 数値: 正規化される入力値
start 数値: 値の現在の範囲の下限
stop 数値: 値の現在の範囲の上限

戻り

Number: 正規化された数値

制約

ボールは、マウスを動かすと少し遅れてついて来ますが、プログラムがボールを赤いボックス内に閉じ込めているので、そこから外に出ることはありません。

let mx = 1; // 円のx位置
let my = 1; // 円のy位置
const easing = 0.05; // イージング
const radius = 24; // 円の半径
const edge = 100;
const inner = edge + radius; // 124

function setup() {
    createCanvas(720, 400);
    noStroke();
    // ellipse(x, y, w, [h])のwとhを半径とするモード
    ellipseMode(RADIUS);
    // rect(x, y, w, h,)のx,yを隅の角の位置、w,hをその対角の隅の位置と解釈する
    rectMode(CORNERS);
}

function draw() {
    background(230);
    // 論理を更新
    update();
    // 描画
    fill(237, 34, 93);
    rect(edge, edge, width - edge, height - edge);
    //fill(200, 100);
    //rect(inner, inner, width - inner, height - inner)
    fill(255);
    ellipse(mx, my, radius, radius);
}

// 論理(変数)を更新する
function update() {
    // マウスと円が十分に近くなければイージングして近づく
    if (abs(mouseX - mx) > 0.1) {
        mx = mx + (mouseX - mx) * easing;
    }
    if (abs(mouseY - my) > 0.1) {
        my = my + (mouseY - my) * easing;
    }
    // 値を最小値と最大値の間に制約する
    mx = constrain(mx, inner, width - inner);
    my = constrain(my, inner, height - inner);;
}

解説

このサンプルの入力は言うまでもなく、マウスの位置です。p5.jsはこれをシステム変数のmouseXとmouseYで取得できます。

ボールがマウスの動きに少し遅れてついて来るのは、イージングと呼ばれるテクニックです。

if (abs(mouseX - mx) > 0.1) {
    mx = mx + (mouseX - mx) * easing;　// イージング
}
if (abs(mouseY - my) > 0.1) {
    my = my + (mouseY - my) * easing;  // イージング 
}

mx = mx + (mouseX – mx) * easing は次のように考えることができます(参照「4_3：応答：イージングの導入 p5.js JavaScript」)。

// 目的地はmouseX
// 残りの距離 (mouseX - mx)
const dx = mouseX - mx;
// 速度は残りの距離に、距離の何分の1かを掛けたもの
const vx = dx * easing;
// 新しい現在位置は、前の現在位置に速度を足したもの
mx = mx + vx;

ただしeasing値は通常1未満なので、その場合には決して目的地に到達しません。人間の見た目には十分到達しているだろうと思える状況になっても、コンピュータは残った微量の距離にeasing値を掛けつづけることになるので、適切なタイミングで計算を停める必要があります。このサンプルの場合には、abs(mouseX – mx) > 0.1 という条件がそれに当たります。

円がボックスの外に出なくしているのは次の２行です。

mx = constrain(mx, inner, width - inner);
my = constrain(my, inner, height - inner);

変数ばかりなので分かりづらいですが、実際の数値を当てはめると容易に理解できます。innerはedge + radius なので、100 + 24 = 124、width – inner は720 – 124 = 596、height – inner は400 – 124 = 276 です。

赤いボックスは、rectMode(CORNERS)設定により、左上隅を(100,100)、右下隅を(620,300)に持つ矩形です。この矩形に対して、円の半径分だけ内向きに入ったスペースの中に押し込みたいわけです。このスペースを描くと下図のようになります。

なお、constrain()を使った２行は、必ずイージングの後に記述します。この順序を逆にすると、円がボックスの外に出てしまいます。位置を制約したいので、新しい位置を計算してからそれを制約するというのがいたって論理的な順番です。

イージング

キャンバスの上でマウスを動かすと、円が少し遅れてついて来ます。アニメーションを描画するフレームとフレームの間、このプログラムは、円とカーソルの位置の差を計算しています。その距離が1ピクセルよりも大きい場合に、円は現在位置からカーソルに向かって、距離の一部(0.05)だけ移動します。

let x = 1;
let y = 1;
// 移動スピードを距離の何分の1にするかを表す数値(0から1までの小数)
const easing = 0.05;

function setup() {
    createCanvas(720, 400);
    noStroke();
}

function draw() {
    background(237, 34, 93);
    // 行先targetXposを決める
    const targetX = mouseX;
    // 描画物から行先までの距離dxを計算する
    const dx = targetX - x;
    // 距離に、距離の何分の1にするかを表すeasingを掛け、スピードvxを求める
    const vx = dx * easing;
    // スピードを現在位置xposに加算する
    x += vx;

    // 同じことを１行でやる
    y = y + (mouseY - y) * easing;
    ellipse(x, y, 66, 66);
}

解説

最近ではテレビ番組のちょっとした部分でも、イージングが使用されているのをよく目にします。これは、Webアニメーションで一時代を築いたFlashの功績だろうと思います。

イージングは、オブジェクトがある位置からある位置に移動するとき、目的地にすぐにではなく少し遅れてから到達したり、だんだん速くなったり(加速)、だんだん遅くなったり(減速)する効果をもたらすテクニックです。アニメーションに加速度の増減要因を設定することで、だんだん速くなったり遅くなったりして目的地に到達する効果が生まれます。

イージングは元々Flash開発者のRobert Pennerが考案したもので、イージング関数と呼ばれる、数学を駆使した関数で実現されます。イージング関数に関する詳細は、当サイトの「11-1 そもそもイージング関数は一体何を…」で触れています。

目的地に近づくにつれてだんだん遅くなるx軸方向へのアニメーションは、次の要領で作成できます。

1. 移動スピードを距離の何分の1にするかを表す数値easing(0から1までの小数)を決める
2. 行先targetXposを決める
3. 描画物から行先までの距離dxを計算する
4. 距離に、距離の何分の1にするかを表すeasingを掛け、スピードvxを求める
5. スピードを現在位置xposに加算する
6. 3,4,5を繰り返す

キーボード

キャンバスをクリックしてそこにフォーカスを与えます。文字キー(a-zのアルファベットのキー)を押すと、時間的空間的に模様が作成できます。それぞれのキーは一意の識別番号を持っていて、空間でのシェイプの位置決めに使用されます。

let rectWidth;  // 矩形の幅

function setup() {
  createCanvas(720, 400);
  noStroke();
  background(230);
  rectWidth = width / 4;  // 矩形の幅はキャンバスの幅の1/4=180
}

function draw() {
  // キー入力を待つ間ループを継続するので、draw()はこのまま置いておく
  // なくても機能するように思えるが。。。
}

function keyPressed() {
  let keyIndex = -1;
  // key: キーボードから入力された直近のキーの値を保持するシステム変数
  // 'a'は97,'z'は122
  // 直近に押されたキーの値が文字キー(a,b,c,d,e,...z)のどれかなら
  if (key >= 'a' && key <= 'z') {
    keyIndex = key.charCodeAt(0) - 'a'.charCodeAt(0);
  }
  // keyIndexが-1のままなら、直近に押されたキーは文字キーでないことになる
  if (keyIndex === -1) {
    // 文字キーでなければ画面をクリアする
    background(230);
  } else {
    // 文字キーなら、矩形を塗る
    const r = random(0, 255);
    const g = random(0, 255);
    const b = random(0, 255);
    // 塗り色をランダムな色にする
    fill(r, g, b);
    // width - rectWidth = 540
    // 0-25の範囲であるkeyIndex値を、0から720の範囲にマッピングする
    // => アルファベットの順番が早いほど左に、遅いほど右に描かれる
    const x = map(keyIndex, 0, 25, 0, width - rectWidth);
    rect(x, 0, rectWidth, height);
  }
}

解説

このサンプルの入力は言うまでもなくキーボードのキーです。説明文の「時間的空間的に模様が作成できる」というのは、キーを押すタイミング(=時間的)とキーの種類(キーによって描く矩形の位置が変わる)によって、さまざまな模様が描ける、ということかと思います。

アート的な視点はさておき、このプログラムの仕様を言うと、aからzまでの文字キーを押すと、キャンバスにサイズが180 x 400 の矩形がランダムな塗りで描画されます。矩形が描画される位置が文字によって、決まっています。また文字キー以外のキーを押すと描画物が消去されます。

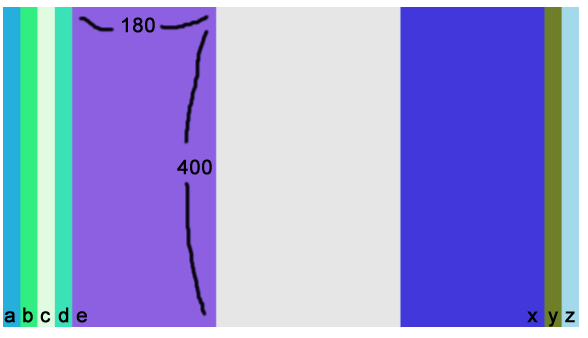
keyPressed()は、キーが押されるたびに１回だけ呼び出される、p5.jsの関数です。キーの長押しを1回とカウントしたいアクションゲームなどで重宝します。

keyはp5.jsのシステム変数で、キーボードから入力された直近のキーの値を持っています。keyPressed()関数の外でも、どこでも使用できます。

文字同士の大小比較

このサンプルで興味を引かれるのは次のifステートメントです。ここでは、key(直近に押されたキーの値)と文字’a’、文字’z’の大小を比べています。これは何を意味しているのでしょう？

let keyIndex = -1;
if (key >= 'a' && key <= 'z') {
    keyIndex = key.charCodeAt(0) - 'a'.charCodeAt(0);
}

MDNの「比較演算子」ページによると、「文字列は Unicode 値を使用した標準的な辞書順に基づいて比較されます」とあります。つまりここでは直近に押されたキーのUnicode値と”a”、”z”のUnicode値の大小が比較されているのです。

このUnicode値(文字セットUnicodeに対してUTF-16形式で割り振られている文字の番号)はp5.jsのunchar()関数で調べることができます(「15：タイポグラフィ(Typography)」)。次のコードは簡単な例です。

outputUnicodeNumber('a', 'b'); // aは97、bは98
print('a' < 'b'); // true

outputUnicodeNumber('あ', 'い'); // あは12354、いは12356
print('あ' < 'い'); // true

outputUnicodeNumber('男', '女'); // 男は30007、女は22899
print('男' < '女'); // false

function outputUnicodeNumber(a, b) {
    print(a + '= ' + unchar(a));
    print(b + '= ' + unchar(b));
}

‘a’と’b’を比べると、’a’のUnicode値は97、’b’のUnicode値は98なので、’a’ < ‘b’はtrueになります。文字同士のこの比較は平仮名でも有効で、上のコードでは’あ’と’い’を比べています。漢字でも有効ですが、’男’ < ‘女’ がfalse になる、という結果には意味が見いだせそうにありません。

つまり、(key >= ‘a’ && key <= ‘z’) という条件は、直近に押されたキーがアルファベットのaからzのどれかなら、という意味なのです。この方法は、押されたキーがアルファベットの文字キーか、またはそれ以外のキーなのかを知りたい場合に利用できます。

そして直近に押されたキーがアルファベットのキーである場合には、’a’とのUnicode値の’差’を変数keyIndexに代入しています。これによって差は、アルファベット並びで早いものほど小さく、遅いものほど大きくなります。

なおkey.charCodeAt(0)のcharCodeAt()は、JavaScriptのString.charCodeAt()メソッドです。keyは文字列なのでcharCodeAt()が使用できます。この行はunchar()関数で書き換えることもできます。

keyIndex = unchar(key) - unchar('a');

マウス 1D

マウスを左右に動かすと、２つの矩形のバランスが変化します。ここではmouseX変数を、矩形のサイズと色の両方の制御に使用しています。

function setup() {
    createCanvas(720, 400);
    noStroke();
    // /矩形を、デフォルトの左上隅ではなくセンターから描画する
    rectMode(CENTER);
}

function draw() {
    background(230);
    // 水平方向のmouseXの値を、垂直方向に置き換える
    let r1 = map(mouseX, 0, width, 0, height);
    // r2はr1が大きくなれば小さく、r1が小さくなれば大きくなる
    let r2 = height - r1;

    // マウスのx位置が左ほど薄く、右ほど濃くなる
    fill(237, 34, 93, r1);
    // マウスのx位置が左ほど小さく、右ほど大きくなる
    rect(width / 2 + r1 / 2, height / 2, r1, r1);

    // マウスのx位置が右ほど薄く、左ほど濃くなる
    fill(237, 34, 93, r2);
    // マウスのx位置が左ほど大きく、右ほど小さくなる
    rect(width / 2 - r2 / 2, height / 2, r2, r2);
}

解説

このサンプルの入力はマウスのx位置です。タイトルについている1Dは”one dimension” のことで、日本語では１次元と訳されます。次元と言うとSFの世界のようなニュアンスがありますが、数学で言う次元には「空間上の点の位置を一意に指定するための座標の数」という意味があります。

１次元は簡単に言うと座標軸が１つ、ということで、このサンプルの場合にはX軸です。このプログラムは、mouseXがもたらすX軸方向のマウスの位置を受け取り、２つの矩形の描画を変化させます。

このサンプルのコード自体は難しいものではありませんが、数学のセンスにあふれています。

draw()関数内の次の行では、まず水平方向のmouseXの値を垂直方向に置き換え、その値を変数r1に代入しています。これによりr1は、マウスがキャンバスの左端にあるとき0になり、キャンバスのセンターにあるとき200(heightの半分)、キャンバスの右端にあるときに400になります。

let r1 = map(mouseX, 0, width, 0, height);

そして次の行では、キャンバスの高さからr1を引いたものをr2としています。これは、r1が大きくなればr2は小さく、r1が小さくなればr2は大きくなるということです。その最大値はheightです。

let r2 = height - r1;

そのr1とr2を使って、矩形が作られます。次の２行では、マウスが左へ行くほど小さく薄くなり、右ほど大きく濃くなる矩形が作成されます。これは、点(width / 2 + r1 / 2, height / 2)を中心とする、一辺がr1の右の正方形です。

// 右の矩形
fill(237, 34, 93, r1);
rect(width / 2 + r1 / 2, height / 2, r1, r1);

同様に、次のコードでr2を使って矩形が作られます。これは右の矩形とは正反対の動きと色の変化を見せます。

// 左の矩形
fill(237, 34, 93, r2);
rect(width / 2 - r2 / 2, height / 2, r2, r2);

マウス 2D

マウスを動かすと、ボックスの位置とサイズが変わります。

function setup() {
    createCanvas(720, 400);
    noStroke();
    rectMode(CENTER);
}

function draw() {
    background(230);
    fill(244, 122, 158);
    rect(mouseX, height / 2, mouseY / 2 + 10, mouseY / 2 + 10);
    fill(237, 34, 93);
    let inverseX = width - mouseX;
    let inverseY = height - mouseY;
    rect(inverseX, height / 2, inverseY / 2 + 10, inverseY / 2 + 10);
}

解説

タイトルの2Dは２次元を意味しています。次元は変化できる方向の数(座標軸の数)を意味します。今の場合はXとY軸です。入力はマウスのx位置とy位置です。

次のrect()関数は、(mouseX, height / 2)を中心とする、一辺が mouseY / 2 + 10 の正方形を描画します。ここからは、位置はmouseXで決まり、大きさはmouseYで決まるということが分かります。

rect(mouseX, height / 2, mouseY / 2 + 10, mouseY / 2 + 10);

下図ではこの矩形だけを描画しています。矩形内の黒丸は矩形の中心点です。マウスを左に動かすと矩形は左に移動し、上に動かすと小さくなります。また右に動かすと右に移動し、下に動かすと大きくなります。

一方、次のrect()関数は、(width – mouseX, height / 2)を中心とする、一辺が(height – mouseY)/2 + 10 の正方形を描画します。

let inverseX = width - mouseX;
let inverseY = height - mouseY;
rect(inverseX, height / 2, inverseY / 2 + 10, inverseY / 2 + 10);

inverseXは幅からmouseXを引いた値なので、mouseXが大きくなると小さくなり、mouseXが小さくなると大きくなります。inverseYも同様です。したがって下図に示すように、薄赤色の矩形とは正反対に動き、大きさも正反対になります。

マウスボタンの押し下げ

マウスを動かすと赤い十字のシェイプも移動し、軌跡が描かれます。マウスボタンを押すと白に変わり、ドラッグで白い十字の模様が描画できます。

function setup() {
    createCanvas(720, 400);
    background(230);
    strokeWeight(2);
}

function draw() {
    // マウスがおされている状態なら
    if (mouseIsPressed) {
        // 線の色を白に
        stroke(255);
        // そうでないなら
    }
    else {
        // 線の色を赤に
        stroke(237, 34, 93);
    }
    // マウスの位置を基準に十字の線を描く
    drawCross(mouseX, mouseY);
}

// マウスカーソルを中心とする、長さがhalfLength*2の十字線を描く
function drawCross(x, y) {
    const halfLength = 66;
    line(x - halfLength, y, x + halfLength, y);
    line(x, y - halfLength, x, y + halfLength);
}

解説

このサンプルの入力もマウスの位置です。マウスにはまた、マウスボタンが押し下げられているかどうかという状態もあり、これも入力に使用できます。p5.jsのシステム変数であるmouseIsPressedについては「4_4：応答：クリック p5.js JavaScript」で述べています。

マウス関数

ボックスをクリックして画面上をドラッグします。

let bx; // ボックスの中心x位置
let by; // ボックスの中心y位置
const boxSize = 75; // ボックスの幅と高さ
let overBox = false; // マウスがボックスの上に重なっているかどうか
let locked = false; // ドラッグ中であるかどうか
let xOffset = 0.0;
let yOffset = 0.0;

function setup() {
    createCanvas(720, 400);
    bx = width / 2.0;
    by = height / 2.0;
    // rect()最初の2つのパラメータを矩形の中心点として使用し、
    // 3つめと4つめのパラメータを矩形の幅と高さの半分として使用するモード
    rectMode(RADIUS);
    strokeWeight(2);
}

function draw() {
    background(237, 34, 93);

    // マウスカーソルがボックスと重なっているなら
    if (
        mouseX > bx - boxSize &&
        mouseX < bx + boxSize &&
        mouseY > by - boxSize &&
        mouseY < by + boxSize
    ) {
        // overBox変数をtrueにする
        overBox = true;
        // ドラッグ状態でないなら
        if (!locked) {
            // 線を白、塗りをピンクにする
            stroke(255);
            fill(244, 122, 158);
        }
        // マウスカーソルがボックスと重なっていないなら
    }
    else {
        // 線を青、塗りをピンクにする
        stroke(156, 39, 176);
        fill(244, 122, 158);
        overBox = false;
    }

    // (bx,by)を中心とする、一辺がboxSize*2の正方形を描く
    rect(bx, by, boxSize, boxSize);
}

// キャンバスだけでなく、ページのどこかをマウスプレスすると１回呼び出される
// 長押ししても呼び出されるのは1回だけ
function mousePressed() {
    print('マウスボタンが押された');
    // マウスカーソルがボックスと重なっているなら
    if (overBox) {
        // ドラッグ状態である
        locked = true;
        // 塗りを白に
        fill(255, 255, 255);
        // マウスカーソルがボックスと重なっていないなら
    }
    else {
        // ドラッグ状態でない
        locked = false;
    }
    // マウスの位置とボックスの中心位置との差を計算
    xOffset = mouseX - bx;
    yOffset = mouseY - by;
}

// マウスが移動しかつマウスボタンが押されている状態のたびに１回呼び出される
// => ドラッグ中何度も呼び出される
function mouseDragged() {
    print('ドラッグ中');
    // ドラッグ状態なら
    if (locked) {
        // ボックスの中心を設定
        bx = mouseX - xOffset;
        by = mouseY - yOffset;
    }
}

// マウスボタンが放されるたびに呼び出される
function mouseReleased() {
    // ドラッグ状態でない
    locked = false;
}

解説

このサンプルの入力はマウス位置と、マウスを使ったプログラムへのユーザーの働きかけです。具体的には、マウスボタンの押し下げと解放、マウスの移動という３つの働きかけを入力として使用しています。

マウスボタンが押し下げられると、JavaScriptで言うmousedownイベントが発生します。p5.jsはこれを受け取り、自身の関数であるmousePressed()を呼び出します。

押し下げられたマウスボタンが放されると、mouseupイベントが発生します。p5.jsはこれを受け取り、自身の関数であるmouseReleased()を呼び出します。

マウスが移動するとその移動中にmousemoveイベントが発生します。p5.jsはこれを受け取り、マウスボタンが押し下げられていない場合には、自身の関数であるmouseMoved()を呼び出し、マウスボタンが押し下げられている場合には、自身の関数であるmouseDragged()を呼び出します。

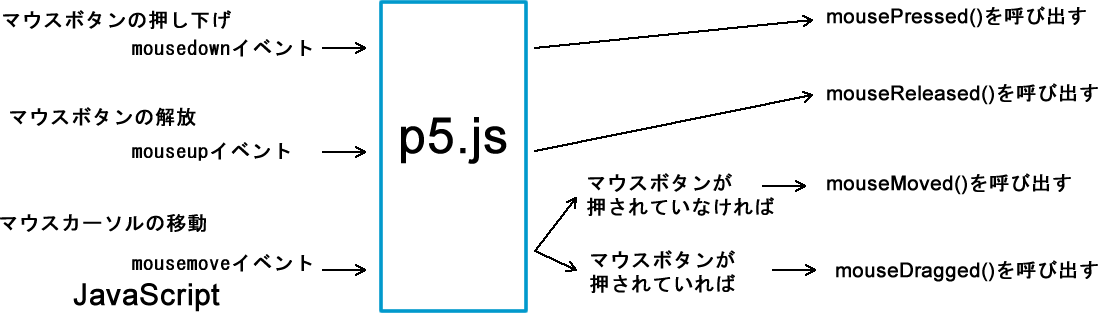
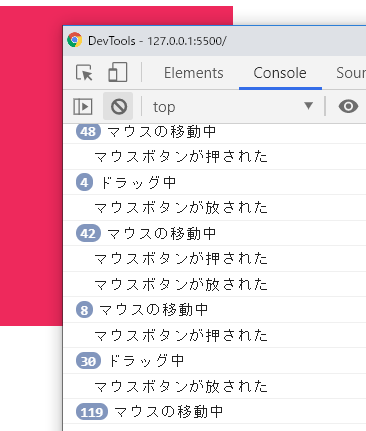
次のコードは、これらのマウスイベントの発生をp5.jsの関数でとらえて、発生のタイミングをprint()関数で出力する例です。関数が呼び出されたことを分かりやすくするためにp5.jsのcursor()関数を使って、カーソルの形を変えています。

function setup() {
  createCanvas(720, 400);
}

function draw() {
  background(237, 34, 93);
}

function mousePressed(event) {
  print('マウスボタンが押された');
  //print(event);
  cursor(HAND);
}

// mousemoveイベント
function mouseDragged() {
  print('ドラッグ中');
  cursor(MOVE);
}

function mouseMoved() {
  print('マウスの移動中');
  cursor(MOVE);
}

function mouseReleased() {
  print('マウスボタンが放された');
  cursor(ARROW);
}

ドラッグするということ

p5.jsはHTMLの<canvas>要素への描画を行うライブラリなので、矩形のドラッグと言っても、”それ”をつまんで引きずるわけではなく、マウスの移動に合わせてドラッグしているように描画することがドラッグするということになります。

p5.js流の矩形のドラッグは次の手順で行えます。

1. マウスダウン時に、マウスカーソルが矩形の中にあるかどうかを調べ、ある場合にはドラッグ用変数をtrueにする
2. このとき同時に、矩形の中心とマウス位置の差分を変数に保持する
3. マウスアップ時に、ドラッグ用変数をfalseにする
4. draw()関数内で、ドラッグ用変数がtrueの場合に、矩形の中心位置をマウス位置と差分の合計に設定する

次のコードは、矩形をドラッグする簡単な例です。

let boxSize = 75;
let bx, by;

let xOffset = 0;
let yOffset = 0;
let dragging = false;

function setup() {
    createCanvas(720, 400);
    rectMode(RADIUS);
    bx = width / 2.0;
    by = height / 2.0;
    rect(bx, by, boxSize, boxSize);
}

function draw() {
    background(237, 34, 93);
    update();
    rect(bx, by, boxSize, boxSize);
}

function update() {
    // ドラッグ中の円の位置
    if (dragging) {
        // 矩形の中心とマウス位置の差分を維持しつつ、矩形をマウス位置に描画
        // => マウスで矩形をつかんだ位置でドラッグできる(矩形センターや左上隅に吸着したりしない)
        bx = mouseX + offsetX;
        by = mouseY + offsetY;
    }
}

function mousePressed() {
    print('マウスボタンが押された');
    if (mouseX > bx - boxSize && mouseX < bx + boxSize && mouseY > by - boxSize && mouseY < by + boxSize) {
        dragging = true;
        // 矩形の中心とマウス位置の差分
        offsetX = bx - mouseX;
        offsetY = by - mouseY;
        cursor(HAND);
    }
}

function mouseReleased() {
    print('マウスボタンが放された');
    dragging = false;
    cursor(ARROW);
}

リファレンスメモ

mousePressed()

説明

mousePressed()関数は、マウスボタンが押し下げられるたびに１回呼び出されます。mouseButton変数は押されたボタンを調べたいときに使用できます。mousePressed()関数が定義されていない場合には、touchStarted()が定義されていれば代わりにこれが呼び出されます。

ブラウザには、さまざまなマウスイベントに関連付けられた異なるデフォルトの振る舞いがあります。このイベントのデフォルトの振る舞いを避けたい場合には、関数の最後に”return false”を加えます。

mouseDragged()

説明

mouseDragged()関数は、マウスが移動中でマウスボタンが押し下げられるたびに１回呼び出されます。mouseDragged()関数が定義されていない場合には、touchMoved()が定義されていれば代わりにこれが呼び出されます。

ブラウザには、さまざまなマウスイベントに関連付けられた異なるデフォルトの振る舞いがあります。このイベントのデフォルトの振る舞いを避けたい場合には、関数の最後に”return false”を加えます。

mouseReleased()
mouseReleased()関数は、マウスボタンが放されるたびに呼び出されます。mouseReleased()関数が定義されていない場合には、touchEnded()が定義されていれば代わりにこれが呼び出されます。

ブラウザには、さまざまなマウスイベントに関連付けられた異なるデフォルトの振る舞いがあります。このイベントのデフォルトの振る舞いを避けたい場合には、関数の最後に”return false”を加えます。