プログラミング はじめの一歩 JavaScript + p5.js編
9：番外編　新しいものを指定数分だけ覚える

本稿は、毎日新聞の「プログラミング・はじめの一歩」とは関係のないオリジナル記事です。

概要

ご存知かどうかは分かりませんが、映画「トロン」に出てきたバイクレースに触発されたと思われるゲームが多数あります。２台のバイクが高速で移動し、自バイクが壁に激突したり、相手バイクの描く光跡(黄と緑の線)に衝突するとアウトになるというゲームです。

本稿で注目するのはゲーム性ではなく、バイクの通った後につづく跡です。バイクはキーボートの上下左右の矢印キーで移動させるとして、この跡はどうやって作成すればよいのでしょう？

下図はその方法を探ったプログラムの実行画面です。クリックすると、実際のプログラムが別ウィンドウで開きます。キーボードの上下左右の矢印キーを押すと、先頭の赤い矩形が動きだし、緑の線が後につづきます。黄色の矩形は線の最後です。

論理を考える

いきなり上のプログラムからその論理を考えろと言っても、今回は難しいです。答えを先に言うと、配列を使って新しいものを指定数分だけ覚えておき、古いものはどんどん忘れる、という方法で実現できます。具体的な話に進む前に、配列でよく使用されるデータ構造について見ておきます。

キューとスタック

キューとスタックは、配列などに保持するデータの出し入れのやり方を指すものです。

キュー
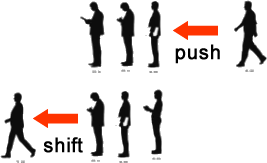
キューは先に入ったものを先に出すやり方です。たとえばATMに並ぶ人の行列は、先に並んだ人から先にお金をおろして列から出ていくのでキューです。キューは日本語で「待ち行列」とも呼ばれます。JavaScriptでは、配列のメソッドを使って、push()してshift()します。

// キュー(待ち行列)　先入れ先出しのリスト構造
// FIFO（First-In-First-Out)の原則
let arr = [1, 2, 3];
// 要素を末尾に追加
arr.push(4);
print(arr); // [1,2,3,4]
// 最初から要素を取り出し、1番めの要素が0番目になるようにキューを進める
arr.shift();
print(arr); // [2,3,4]

push()してshift()は下図のようなイメージです。

スタック
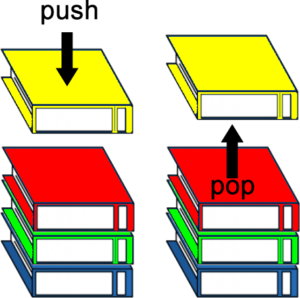
スタックは、後に入れたものを先に出すやり方です。たとえば白菜などの漬物は、先に入れたものの上に層状(スタック)に重なり、後から入れたものから先に取り出すのでスタックです。ブラウザの[戻る]ボタンも、直近のページに戻るのでスタック構造をしています。JavaScriptでは、配列のメソッドを使って、push()してpop()します。

// スタック 後入れ先出しのリスト構造
// LIFO（Last-In-First-Out）の原則
let arr = ['あ', 'い', 'う'];
// 要素を末尾に追加
arr.push('え');
print(arr); // ["あ", "い", "う", "え"]
// 末尾から要素を取り出す
arr.pop();
print(arr); // ["あ", "い", "う"]

push()してpop()は下図のようなイメージです。

新しいものを指定数分だけ覚える

配列を使った、新しいものを指定数分だけ覚えるという論理を言葉で考えてみましょう。

まず、配列には「新しいもの」を追加するので、追加する要素は、インデックス番号が0になる先頭に置くのが分かりやすい処理でしょう。

次の「指定数分だけ覚える」についてはどうでしょう？　「覚える」というのは配列に保持する、ということですが、「指定数分だけ」というのはどう考えればよいでしょう？　たとえば5が指定されれば、覚えるのは5個です。この場合5は配列の要素数、つまり配列の長さに当たります。「指定数分だけ覚える」は、要素を最大で5個保持しつづける、要素数が5個を超えたら一番古いものを削除する、に言い換えることができます。

1. 配列の先頭に要素を追加する
2. もし配列の長さが指定数よりも大きいなら
3. 配列の最後を削除する

この論理をコードで表すと次のように記述できます。

// 指定された数
let num = 5;
// 要素を5つ持つ配列
let array5 = [1, 2, 3, 4, 5];
// 最初の配列
print(array5);
// 先頭に6を追加
array5.unshift(6);
print(array5);
// 配列の長さは6で、numより大きい
if (array5.length > num) {
    // 最後の要素を削除
    array5.pop();
}
print(array5);

Array.unshift()は配列の先頭に要素を追加するメソッドで、Array.pop()は配列の最後の要素を削除するメソッドです。配列の長さが5より大きい場合に、配列の最後の要素が削除されます。

論理のテスト

この論理が本当に正しいのかをテストしてみましょう。次のコードでは、p5.jsのテキストフィールドを作成し、入力が確定した時点で、配列の操作を行っています。比較のため、要素を先頭に追加しつづける配列noLimitMemoryも作成しています。

let noLimitMemory = [];
let memoryNum = 5;
let memory5_1 = [];

function setup() {
    createCanvas(400, 300);

    // テキストフィールドを作成
    const textInput = createInput('');

    // テキストフィールドの入力が確定し(Enterキーが押され)たら
    textInput.elt.onchange = function() {
        // いくつでも記憶する。新しいものが先に来る。
        // 配列の先頭に要素を追加
        noLimitMemory.unshift(textInput.value());

        // 5つだけ覚える
        // 配列の先頭に要素を追加
        memory5_1.unshift(textInput.value());
        if (memory5_1.length > memoryNum) {
            // 配列の最後の要素を削除
            memory5_1.pop();
        }

        print(noLimitMemory);
        print(memory5_1)
            // テキストフィールドをクリア
        textInput.value('');
    };
}

下図はテキストフィールドにa,b,c,d,e,f,gの順で文字を入力したときの結果です。noLimitMemoryの要素は増える一方ですが、memory5_1配列の要素数は5に制限され、最後の要素が作字されているのが分かります。

shift()とunshift()はpush()、pop()よりも処理に時間がかかる

Array.push()メソッドは配列の最後に要素を追加し、Array.pop()は配列の最後の要素を削除します。一方、Array.unshift()は配列の最初に要素を追加し、Array.shift()は配列の最初の要素を削除します。push()/pop()とunshift()/shift()は配列の端にある要素に作用しますが、配列の先頭要素を扱うときには、後の要素のインデックス番号を付けなおす必要があるので、その分、shift()とunshift()はpush()、pop()よりも処理に時間がかかります。

配列のメソッドを使わない方法

配列のメソッドを使わない方法もあります。次のコードを前のテキストフィールドのコードに組み込むと、memory5_1配列と同じ結果を得ることができます。

for (let i = memoryNum - 1; i > 0; i--) {
    // 要素を１つ右に移動
    memory5_2[i] = memory5_2[i - 1];
}
// 最初の要素として、最新の値を割り当てる
memory5_2[0] = textInput.value();

これは、配列要素を後ろから走査して、要素の位置を右にコピーしてから、最初の要素を最新の値で上書きする方法です。大きな特徴は、配列のメソッドを通さず、要素の値を直接操作するので、高速に動作することです。

トロン風を実装

では、「概要」で示したトロン風の光跡を作るコードを見ていきます。これまでは要素が5個未満の例を見てきましたが、次のトロン風では、100個と一気に増えています。

// トロン風

let memoryNum = 100; // 記憶できる数
let xpos = []; // x位置を保持する配列
let ypos = []; // y位置を保持する配列
const speed = 5; // スピード

function setup() {
    createCanvas(400, 300);
    // xposとyposにmemoryNum分だけ初期値を入れる
    for (let i = 0; i < memoryNum; i++) {
        xpos[i] = width / 2;
        ypos[i] = height / 2;
    }
    noStroke();
}

function draw() {
        background(0);
        // 更新してから描画
        update();
        display();
    }
    // 描画
function display() {
    for (let i = 0; i < memoryNum; i++) {
        // 先頭は赤、末尾は黄色、ほかは緑
        if (i === 0) {
            fill(255, 0, 0);
        }
        else if (i === memoryNum - 1) {
            fill(255, 255, 0);
        }
        else {
            // 後のものほど薄くする
            fill(83, 240, 120, 255 - i * 2.5);
        }
        // 矩形を描画
        rect(xpos[i], ypos[i], 10, 10);
    }
}

// 更新の論理
function update() {
    // 変更するのはキーが押されている間だけ
    if (keyIsPressed) {
        // 配列のメソッドを使わない方法
        // 要素を１つ右にコピー
        for (let i = memoryNum - 1; i > 0; i--) {
            xpos[i] = xpos[i - 1];
            ypos[i] = ypos[i - 1];
        }

        // 上下左右キーの押し下げで配列の最初の要素を新しい値で上書き
        // 右キー
        if (keyCode === RIGHT_ARROW) {
            xpos[0] = xpos[0] + speed;
            // 左キー
        }
        else if (keyCode === LEFT_ARROW) {
            xpos[0] = xpos[0] - speed;
            // 上キー
        }
        else if (keyCode === UP_ARROW) {
            ypos[0] = ypos[0] - speed;
            // 下キー
        }
        else if (keyCode === DOWN_ARROW) {
            ypos[0] = ypos[0] + speed;
        }
    }
}

プログラムコードを実行順に追っていきましょう。p5.jsではまず、関数外のコードが実行されます。今の場合で言うと、変数memoryNumが数値100で初期化され、xposとyposという名前の配列が作成され、変数speedが数値5で初期化されます。

let memoryNum = 5; // 記憶できる数
let xpos = []; // x位置を保持する配列
let ypos = []; // y位置を保持する配列
const speed = 5; // スピード

次にsetup()関数が呼び出されます。ここでは配列のxposとyposにmemoryNum個の200と150を入れています。200はキャンバスの幅の半分、150はキャンバスの高さの半分です。xposとyposは矩形の描画位置に使用します。

// xposとyposにmemoryNum分だけ初期値を入れる
for (let i = 0; i < memoryNum; i++) {
    xpos[i] = width / 2;
    ypos[i] = height / 2;
}

その次はdraw()関数が呼び出されます。ここではupdate()関数を呼び出しています。update()は描画の論理を更新する関数で、実際の描画を行うdisplay()関数より先に呼び出します。

update()のコードは、何らかのキーが押し下げられている間だけ実行されます。p5.jsのキーについては「4_6：応答：キー p5.js JavaScript」で述べています。

関数内ではまず、前述した配列のメソッドを使わない方法でxposとyposに含まれる値を１つ右にコピーしています。分かりづらい場合には、memoryNumにもっと小さな5などの値を入れて、変化前と右にコピーした後、最初の値を上書きした後のxposを、キーボードの右矢印キーを押して出力して確認します。

if (keyIsPressed) {
    // 配列のメソッドを使わない方法
    // 要素を１つ右にコピー
    print('変化前のxpos');
    print(xpos);

    for (let i = memoryNum - 1; i > 0; i--) {
        xpos[i] = xpos[i - 1];
        ypos[i] = ypos[i - 1];
    }
    print('右にコピー');
    print(xpos);

xposとyposの1つ右へのコピーが終わったら、最初の要素の値を上書きします。このとき押されたキーによってxposとyposの最初とする値を変えています。これにより右矢印キーを押したときには右に、上矢印キーを押したときには上に、矩形が描かれるようになります。

    // 上下左右キーの押し下げで配列の最初の要素を新しい値で上書き
    // 右キー
    if (keyCode === RIGHT_ARROW) {
        xpos[0] = xpos[0] + speed;
        // 左キー
    }
    else if (keyCode === LEFT_ARROW) {
        xpos[0] = xpos[0] - speed;
        // 上キー
    }
    else if (keyCode === UP_ARROW) {
        ypos[0] = ypos[0] - speed;
        // 下キー
    }
    else if (keyCode === DOWN_ARROW) {
        ypos[0] = ypos[0] + speed;
    }
    print('最初の値を上書き');
    print(xpos);
}

update()関数の実行が終わったら、実際の描画を行うdisplay()関数が呼び出されます。ここでは最初の矩形を赤、最後を黄、そのほかの緑に色分けして、rect()関数で矩形を描画しています。緑を指定するfill()関数では、4つめの引数でアルファ値を与え、後で描かれる矩形ほど透明度を高くしています。これにより、彗星の尾のような効果が生まれます。

// 後のものほど薄くする
fill(83, 240, 120, 255 - i * 2.5);

トロン風の光跡は、分かってしまえばそう難しい論理で作られているわけではないことが分かります。