この記事の詳しい内容には毎日新聞の「矢印で命令をつなぐ」ページから有料記事に進むことで読めます。
目次
概要
命令された通りに、カードに絵をかくロボットがいます。ロボットは命令をフローチャートで受け取ります。
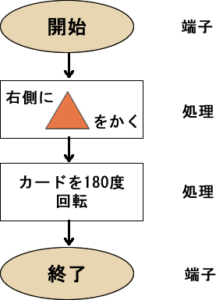
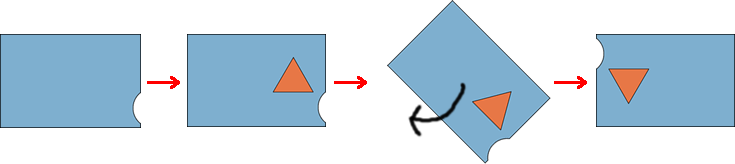
上図のフローチャートでは、カードの右側に三角を書いてカードを180度回転させるので、結果は下図のように、カードの切り欠きが左上にきて、三角は逆さになって左側にきます。
そこで問題です。ロボットが下図のフローチャート通りにカードに絵をかいたとき、カードを180度回転した直後のカードの見た目はどのようになっているでしょう?
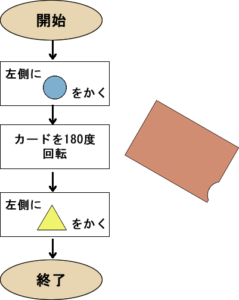
論理を考える
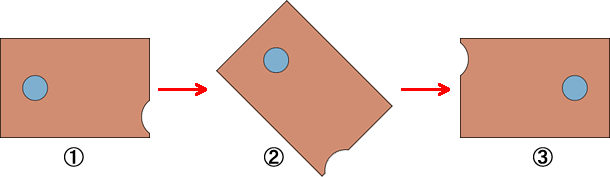
カードの左側に青丸を描き(下図の(1))、それを時計回りに180度回転((2))させた直後は、黄色の三角を描く前なので、カードの見た目は下図の(3)のようになっているはずです。実際に紙に丸を書いて紙の中心で右回りに180度回してみると分かります。
では、概要の例も含め、JavaScriptとp5.jsでプログラミングしていきましょう。
やっかいな回転
通常ですと、論理を[コンソール]に出力し、論理が固まってから視覚化に進みますが、今回は回転が絡むので、初めから描画していくことにします。
まず、カードには切り欠きがあります。これは回転したことを分かりやすくするためのものなのですが、切り欠きをコードで作成するのは大変なので、画像ファイルのイメージで表現することにします。カード以外の円や三角はコードから作成します。
カードの上に円をかくということは、p5.jsの場合、カードを描画して、カードに重なる位置に円を後から描画することです。後から描くことで、カードが奥、円が手前にあるように見えます。
ではカードを180度回転させるとは、どういうことでしょう? 実世界でカードを回転させると、そこにかいた円もいっしょに回転するので、イメージのカードにかいた円もカードといっしょに回転させるのが妥当でしょう。
180度回すことは簡単なように思われます。たとえば通常の描画アプリでは、画像を選んで回転ツールを操作するだけです。

JavaScriptでもHTML要素の回転は簡単です。次のコードは、p5.jsのcreateImg()関数を使って<img>要素を作成し、ボタンのクリックで180度回転させる例です。
// html要素の回転は簡単
function setup() {
noCanvas();
const imgElement = createImg('images/sayaka_isoyama.png');
// [回転!]ボタン
const rotateButton = setButton('回転', {
x: 220,
y: 10
});
// マウスプレスで、<img>要素を180度回転させる
rotateButton.mousePressed(() => {
// <img>要素のCSSスタイルをJavaScriptから操作する
imgElement.elt.style.transform = 'rotate(' + 180 + 'deg)';
});
}
function setButton(label, pos) {
const button = createButton(label);
button.size(80, 40);
button.position(pos.x, pos.y);
return button;
}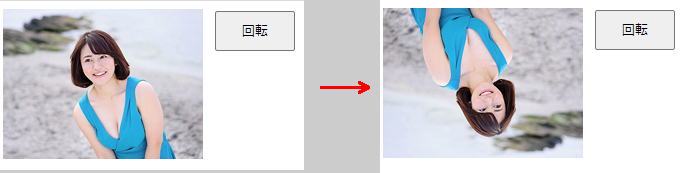
しかし、本稿でやろうとしているのは、HTMLの<canvas>要素に描いている描画物の一部の回転です。これは上記コードのように要素のスタイルを変えることでは行えません。上記の方法を<canvas>要素に適用すると、<canvas>要素そのものが回転します。
<canvas>要素の描画物(イメージや円や三角など)を回転させるには変換(座標変換、transform)を使用します。具体的にはp5.jsのtranslate()とrotate()関数を使用します。
座標変換の回転を理解する
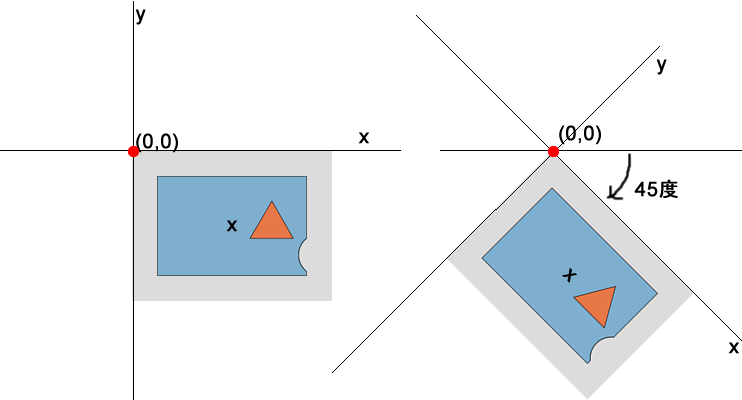
座標変換の回転は、キャンバスの原点をピン留めした状態で右回り(正の角度)に行われます。これはキャンバスの座標システム(X軸とY軸)が傾くという大事件です。傾きの角度はX軸の正方向(真右)を0度として時計回りにスタートします。下図はrotate(45)で45度傾けた例です
キャンバスの原点は座標変換の移動(平行移動)で移すことができます。移動で原点を回転の中心に移してから、回転を行うと、回転は新しい原点を中心に行われます。
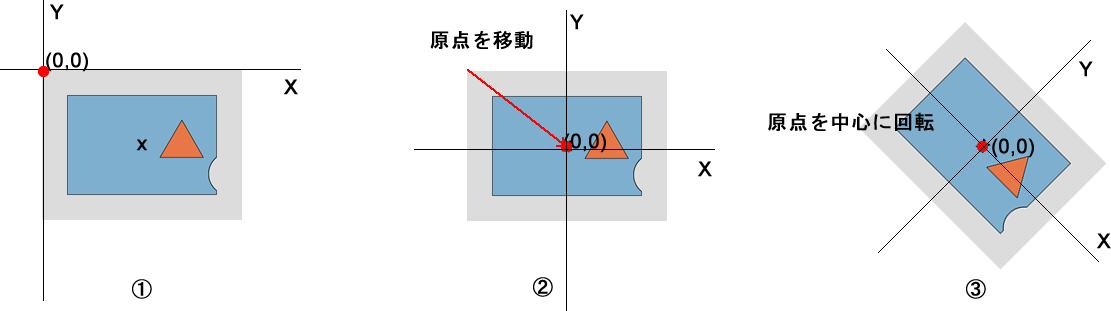
次のコードは、カードがキャンバスセンターを中心に回転する例です。
// 移動 => 回転の基本
let card; // カードのイメージ
let angle = 0; // 座標回転の角度
let centerX; // 回転の中心にする(x,y)座標
let centerY;
function preload() {
card = loadImage('images/card.png');
}
function setup() {
createCanvas(400, 300);
// 角度をラジアン単位で指定する関数を度単位で指定できるようにする
// rotate(度数)
angleMode(DEGREES);
// イメージをそのセンターから描画するようにする
imageMode(CENTER);
// 回転の中心を決める。この場合はキャンバスセンター
centerX = width / 2;
centerY = height / 2;
// 円の塗り色
fill(color(200, 0, 0));
}
function draw() {
background(220);
// 原点をキャンバスセンターに移す
translate(centerX, centerY);
// キャンバスセンターを基準にangle度座標システムを回転させる
rotate(angle);
// 原点は(centerX, centerY)に移動しているので、
// カードを(centerX, centerY)に描くには、(x,y)を(0,0)にする
image(card, 0, 0);
// 回転の中心を示す赤い円
ellipse(0, 0, 10, 10);
angle++;
}カードのイメージがキャンバスセンターを中心に時計回りにつづけて回転します。
コードを上から見ていきましょう。変数angleはdraw()関数内で1ずつ大きくし、回転の角度に使用します。centerXとcenterYは回転の中心位置を示す座標に使用します。
setup()関数内のangleMode()関数は角度をラジアン単位で指定するか(デフォルト)、度単位で指定するかを決めます。rotate()やsin()、cos()などの関数はラジアン単位の値を取ります。ラジアン単位ではピンとこない場合には、angleMode(DEGREES)を呼び出しておくと、慣れた度が使用できます。このおかげで変数angleには1(度)が指定できます。
イメージはデフォルトでその左上隅を基準に描画されますが、imageMode(CENTER)を呼び出しておくと、image()関数に渡す(x,y)値をイメージのセンターとすることができるので、イメージをそのセンターで回転させたいときに便利です。
centerXとcenterYにはキャンバスのセンターに当たる値を指定しています。
変換を適用するのはdraw()関数内です。まず translate(centerX, centerY)によって、座標システムの原点がキャンバスのセンターに移ります。そしてrotate(angle)によって、座標システムがangle度だけ時計回りに回転します。angleは1フレームで1ずつ大きくなるので、キャンバスは1度ずつ傾いていくわけです。
そしてimage(card, 0, 0)でカードを描いています。(0,0)は座標の原点を意味するので、この0,0には違和感があるかもしれません。しかし原点は、translate(centerX, centerY)によって(centerX, centerY)に移動しているので、0,0は前の原点から見ると、centerX, centerYなのです。imageMode(CENTER)によって、image(card, 0, 0)で描かれるカードは(0,0)をセンターとして描かれるので、カードは(0,0)を中心に回転することになります。
最後のellipse(0, 0, 10, 10)は回転の中心を示すための赤い円を描画しています。変換はこの円にも及ぶので、円の座標は(0,0)です(これも前の原点から見ると、centerX, centerの位置にあります)。
何らかの理由で、描画にcenterX, centerYを使用したい場合には、rotate()の後、translate(-centerX, -centerY)を呼び出して、原点を通常の原点に戻します。
// 原点をキャンバスセンターに移す
translate(centerX, centerY);
// キャンバスセンターを基準にangle度座標システムを回転させる
rotate(angle);
// 原点を元に戻す
translate(-centerX, -centerY);
image(card, centerX, centerY)
ellipse(centerX, centerY, 10, 10);* 変換はdraw()関数の呼び出しごとにリセットされて適用されます。移動と回転については、「5_1:移動(translate) p5.js JavaScript」、「5_2:回転(rotate) p5.js JavaScript」、「5_3:移動(translate)と回転(rotate) p5.js JavaScript」で詳しく述べています。
右側に三角をかいてカードを180度回転する
では、お題の例にあった「右側に三角をかいてカードを180度回転する」を表現するプログラムを見ていきましょう。
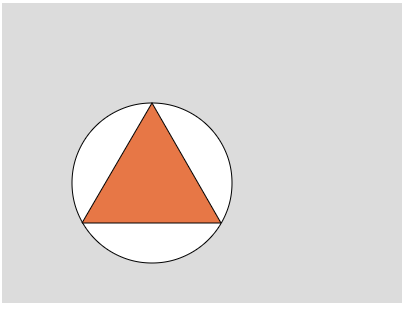
ここで少し問題になるのが、三角形をどうやって描くかです。p5.jsには三角形を描画するtriangle()関数があり、これが使用できます。しかしこの関数は引数として三角形の3つの頂点の座標を取るので、ある決めた位置に正三角形を描きたい場合、triangle()を呼び出す前に、3つの頂点の座標を調べておく必要があります。
正三角形の3つの頂点を知る方法はいくつもあるようですが、本稿で取ったのは下図に示す方法です。
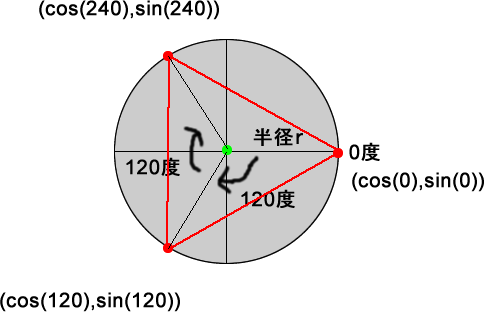
円に接する三角形を想定すると、三角形が正三角形の場合には、円周上を0度、120度、240度進んだところが頂点に当たると考えられます。この3点は次の式で求まります。
// (centerX, centerY)を中心とする半径がradiusの円
// 円周上のx座標値
const x = centerX + cosValue * radius;
// 円周上のy座標値
const y = centerY + sinValue * radius;* 円とサイン、コサインの関係は「7_6:円運動 p5.js JavaScript」で述べています。
これをもとに、円の中心座標と半径を受け取り、そこから正三角形の3つの頂点座標を計算して返す関数は次のように定義できます。
// 円の中心座標と半径を受け取り、そこから正三角形の3つの頂点座標を計算して返す
function getTrianglePoinsts(centerX, centerY, radius) {
let result = []; // 結果を入れる配列
let angle = -90; // 角度は-90度(真上の角度)から始める
// 3回繰り返す
for (let i = 0; i < 3; i++) {
// 角度のコサインとサイン値を得る
const cosValue = cos(angle);
const sinValue = sin(angle);
// (centerX,centerY)を中心とする半径radiusの円周周上のxとy座標
const x = centerX + cosValue * radius;
// 円周上のy座標値
const y = centerY + sinValue * radius;
// (x,y)を配列として結果の配列に追加
result.push([int(x), int(y)]);
// 角度に120度を足す
angle += 120;
}
return result;
}この関数では、正三角形の頂点を真上に持ってくるために、変数angleのスタート値を0でなく、90度分引いた-90にしています。
getTrianglePoinsts()関数は次のように使用します。
function setup() {
createCanvas(400, 300);
angleMode(DEGREES);
background(220);
// (150,100)を中心とする半径80の円
fill(color(255));
ellipse(150, 180, 80 * 2);
fill(color(231, 116, 70));
// (150,100)を中心とする半径80の円に接する正三角形
const points = getTrianglePoinsts(150, 180, 80);
triangle(points[0][0], points[0][1], points[1][0], points[1][1], points[2][0], points[2][1]);
}下図はこの実行結果です。
ここまで見てきた事柄を使用すると、「右側に三角をかいてカードを180度回転するプログラム」は次のように記述できます。
let card; // カードのイメージ
let angle = 180; // 座標回転の角度
let centerX; // 回転の中心にする(x,y)座標
let centerY;
function preload() {
// カードのサイズは00 x 200
card = loadImage('images/card.png');
}
function setup() {
createCanvas(400, 300);
angleMode(DEGREES);
imageMode(CENTER);
centerX = width / 2;
centerY = height / 2;
}
function draw() {
background(220);
// 画面のマウスプレスで変換適用
if (mouseIsPressed) {
// 座標の原点をカードのセンターに移動
translate(centerX, centerY);
// キャンバスセンターを中心に座標システムを180度時計回りに回転
rotate(angle);
// 座標を元の原点(0,0)に戻す
translate(-centerX, -centerY);
}
// 移動 -> 回転 -> 移動した座標システム上で描画
drawCard();
drawTriangle('right');
}
// キャンバスセンターをセンターとしてカードのイメージを描く
function drawCard() {
image(card, centerX, centerY);
}
function drawTriangle(pos) {
fill(color(231, 116, 70));
let x;
if (pos === 'right') {
x = 280
}
else if (pos === 'left') {
x = 80;
}
// 円の中心座標と半径を渡して、正三角形の3つの頂点座標を得る
const points = getTrianglePoinsts(x, width / 2 - 50, 50);
triangle(points[0][0], points[0][1], points[1][0], points[1][1], points[2][0], points[2][1]);
}
// 円の中心座標と半径を受け取り、そこから正三角形の3つの頂点座標を計算して返す
function getTrianglePoinsts(centerX, centerY, radius) {
let result = []; // 結果を入れる配列
let angle = -90; // 角度は-90度(真上の角度)から始める
// 3回繰り返す
for (let i = 0; i < 3; i++) {
// 角度のコサインとサイン値を得る
const cosValue = cos(angle);
const sinValue = sin(angle);
// (centerX,centerY)を中心とする半径radiusの円周周上のxとy座標
const x = centerX + cosValue * radius;
// 円周上のy座標値
const y = centerY + sinValue * radius;
// (x,y)を配列として結果の配列に追加
result.push([int(x), int(y)]);
// 角度に120度を足す
angle += 120;
}
return result;
}下は実行画面です。画面のマウスプレスでカードが180度回転します。
左側に円をかいてカードを180度回転し、左側に三角をかく
つづいて「左側に円をかいてカードを180度回転し、左側に三角をかくプログラム」を見ていきましょう。
実世界で人間が、左側に円をかいてカードを180度回転し、左側に三角をかくと、おそらく下図のように三角の頂点を真上にかくでしょう。
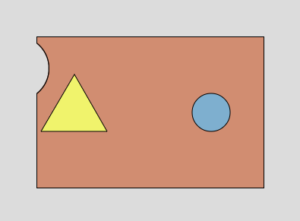
これを、ここまでのプログラミングの立場から考えると、
- カードと円には変換を適用し、三角には適用しない
- カードと円と三角に変換を適用し、三角にはさらに逆の回転を適用する
となります。まずは(1)から見ていきましょう。
カードと円には変換を適用し、三角には適用しない
上図は、カードと円が180度回転し(上下左右が逆になり)、三角は回転していない(左側に描かれ、頂点が真上)ことを示しています。これは、カードと円に変換を適用し、三角には適用しない、ということです。
変換関数(translate()やrotate())を呼び出すと、それ以降のすべての描画はその影響を受けます。これは、描画物すべてに変換を適用したい場合には問題になりませんが、適用したくない描画が含まれるときには問題になります。今の場合、三角は上下左右を逆にしたくないので、変換を適用したくないわけです。
pt.jsには変換が限定できるpop()とpush()という使い勝手のよい関数があります。使い方は簡単で、限定したい変換をpop()とpush()で囲むだけです。pop()とpush()については「5_6:変換状態の保存と復元 p5.js JavaScript」で述べています。
次のコードでは、push()とpop()を使って変換の適用をマウスプレス時に限定しています(提示していないコードは前のものと同じです)。
function draw() {
background(220);
if (mouseIsPressed) {
// 変換の適用範囲を限定---->
push();
translate(centerX, centerY);
rotate(angle);
translate(-centerX, -centerY);
// 変換適用後のカードと円を描画
drawCard();
drawCircle('left');
angle++
pop(); // 変換の適用範囲はここまで---->
}
else {
// 回転なし
angle = 0;
// 変換が適用されないカードと円を描画
drawCard();
drawCircle('left');
}
// 三角には変換は適用されない
drawTriangle('left');
}
// 指定位置に青い円を描く
function drawCircle(pos) {
fill(color(124, 176, 207));
let x;
if (pos === 'right') {
x = 280;
}
else if (pos === 'left') {
x = 120;
}
ellipse(x, height / 2, 50);
}マウスプレスでカードと円は回転しますが、三角はしません。
draw()内のコードは大きく下図の3つに分けることができます。

translate()とrotate()の変換はpop()とpush()関数に囲まれているので、マウスプレス時にしか効果を発揮しません。マウスプレス時もマウスプレス時でないときも同じdrawCard()とdrawCircle(‘left’)を呼び出していますが、前者には変換が適用され、後者には適用されないので、描画結果が異なってきます。三角はマウスプレスと変換に関係のないところで描画しているので、通常通り描画されます。
カードと円と三角に変換を適用し、三角にはさらに逆の回転を適用する
これは結果は同じですが、やり方が異なる方法で、いったん全部に変化を適用し、三角にだけ逆の回転を適用します。draw()の1回の呼び出し中において変換は累積されるので、適用したくない分をマイナスするという発想です。
if (mouseIsPressed) {
push(); // 変換の適用範囲を限定(外側)---->
translate(centerX, centerY);
rotate(angle);
translate(-centerX, -centerY);
// 変換適用後のカードと円を描画
drawCard();
drawCircle('left');
push(); // 変換の適用範囲を限定(内側)---->
translate(centerX, centerY);
rotate(-angle);
translate(-centerX, -centerY);
drawTriangle('left');
pop(); // 変換の適用範囲はここまで(内側)---->
angle++
pop(); // 変換の適用範囲はここまで(外側)---->
}
else {
// 回転なし
angle = 0;
// 変換が適用されないカードと円を描画
drawCard();
drawCircle('left');
drawTriangle('left');
}上記コードでは、push()/pop()がネストされています。外側のpush()/pop()では、translate(centerX, centerY)とrotate(angle)、translate(-centerX, -centerY)がカードと円、三角の描画に適用され、内側のpush()/pop()ではtranslate(centerX, centerY)、rotate(-angle)、translate(-centerX, -centerY)が三角の描画に適用されます。
三角の回転に注目すると、外側のpush()/pop()でrotate(angle)が適用され、内側のpush()/pop()でrotate(-angle)が適用されるので、角度は相殺される(つまり変化しない)ことになります。

左側に円をかいてカードを180度回転し、左側に三角をかくプログラム
お題の答えを得るためのコードはほとんど出来上がっていると言えますが、ワンクリックで円を描画し、カードを180度回転させて三角を描画するプログラムを示しておきます。
次のコードでは、変換を適用する関数を入れる配列と、変換を適用しない配列を新たに設け、そこに関数と引数への参照を持つオブジェクトを追加して、関数を呼び出すという、少しトリッキーな方法を使っています。
let card;
let centerX;
let centerY;
let angle = 0;
let isRotation = false;
let transformFunctions = []; // 変換を適用する関数を入れる配列
let noTransformFunctions = []; // 変換を適用しない関数を入れる配列
function preload() {
card = loadImage('images/card.png');
}
function setup() {
createCanvas(400, 300);
angleMode(DEGREES);
imageMode(CENTER);
centerX = width / 2;
centerY = height / 2;
// drawCardは変換を適用する関数なのでtransformFunctions配列に入れる
// 追加するのは、funcプロパティとargumentsプロパティを持つObjectオブジェクト
transformFunctions.push({
func: drawCard,
arguments: null
});
// [START]ボタン
const startdButton = setButton('START', {
x: 160,
y: 300
});
startdButton.mousePressed(() => {
// transformFunctions配列にdrawCircle('left')を表すオブジェクトを追加
transformFunctions.push({
func: drawCircle,
arguments: 'left'
});
// isRotationをtrueにして変換開始
isRotation = true;
});
}
function draw() {
background(220);
// 変換を適用-----> ここから
push();
if (isRotation) {
translate(centerX, centerY);
rotate(angle);
// 回転を180度で止める
if (angle >= 180) {
angle = 180;
// noTransformFunctions配列に追加するのはdrawTriangle1つ
if (noTransformFunctions.length === 0) {
noTransformFunctions.push({
func: drawTriangle,
arguments: 'left'
});
}
}
else {
angle++;
}
translate(-centerX, -centerY);
}
// 変換を適用する関数に引数を渡して実行する
for (let i = 0; i < transformFunctions.length; i++) {
const obj = transformFunctions[i];
// オブジェクトのfuncプロパティに()をつづけ、argumentsプロパティを渡す
// => 関数に引数を渡して呼び出したことになる
obj.func(obj.arguments);
}
pop(); // 変換を適用------>ここまで
// 変換を適用しない関数に引数を渡して実行する
if (noTransformFunctions.length >= 1) {
for (let i = 0; i < noTransformFunctions.length; i++) {
const obj = noTransformFunctions[i];
obj.func(obj.arguments);
}
}
}
function drawCircle(pos) {
fill(color(124, 176, 207));
let x;
if (pos === 'right') {
x = 280;
}
else if (pos === 'left') {
x = 120;
}
ellipse(x, height / 2, 50);
}
function drawCard() {
image(card, centerX, centerY);
}
function drawTriangle(pos) {
fill(color(243, 241, 107));
let x;
if (pos === 'right') {
x = 280
}
else if (pos === 'left') {
x = 100;
}
const points = getTrianglePoinsts(x, width / 2 - 50, 50);
triangle(points[0][0], points[0][1], points[1][0], points[1][1], points[2][0], points[2][1]);
}
function getTrianglePoinsts(cX, cY, radius) {
let result = [];
let ang = -90;
for (let i = 0; i < 3; i++) {
const cosValue = cos(ang);
const sinValue = sin(ang);
const x = cX + cosValue * radius;
const y = cY + sinValue * radius;
result.push([int(x), int(y)]);
ang += 120;
}
return result;
}
function setButton(label, pos) {
const button = createButton(label);
button.size(120, 50);
button.position(pos.x, pos.y);
return button;
}[START]ボタンをクリックすると、カードの上に青い円が描かれ、カード(と円)が180度回転し、最後に黄色の三角が描かれます。
前述した少しトリッキーな方法について、簡単に述べておきます。配列に入れるのは、funcプロパティとargumentsプロパティを持つObjectオブジェクトです。
transformFunctions.push({ func: drawCircle, arguments: ‘left’ });
funcプロパティには定義してある関数への参照(drawCircle)を割り当てます。これは文字列ではなく、JavaScriptのFunction(関数)オブジェクトを参照する名前です。argumentsプロパティにはその関数に渡す引数を割り当てます。
呼び出すときには、配列からそのオブジェクトのfuncプロパティを参照し、その後にかっこをつづけて、かっこの中に同じオブジェクトのargumentsプロパティを指定します。transformFunctions[0].funcは関数への参照(drawCircle)で、関数への参照につづけるかっこ()は関数を実行するという意味を持ちます。そのかっこ内にtransformFunctions[0].arguments(‘left’)を指定すると、その関数に引数が渡された実行されます(drawCircle(‘left’))。
transformFunctions[0].func(transformFunctions[0].arguments)
JavaScriptの関数はオブジェクトなので、このような使い方もできるわけです。変換を用いる関数や用いない関数が多い場合には、この方法が役立つかもしれません。
カードの上に円と三角を描画する
また別の論理として、p5.jsのp5.Graphicsオブジェクトを使う方法も考えられます。p5.Graphicsオブジェクトは、言わば画面外のキャンバス(オフスクリーンキャンバス)です。キャンバスの外で、p5.Graphicsオブジェクトを使って暫定的な描画作業を行い、それをimage()関数でキャンバスに描画します。
オフスクリーンキャンバスをカードに見立て、オフスクリーンキャンバスで円や三角を描きます。円や三角はカード上に描かれているので、変換を適用しオフスクリーンキャンバスを描画するだけで、カードと円、三角は回転します。オフスクリーンキャンバスについては「1:構造(Structure)」の「グラフィックを作成(p5.Renderer)」で述べています。
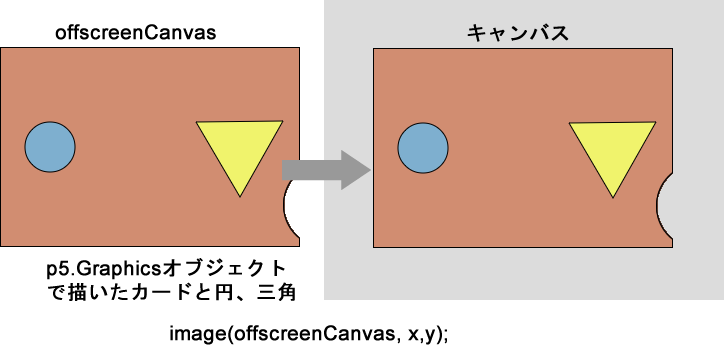
以下はオフスクリーンキャンバスを使ってカードの上に円と三角を描画するプログラムの全コードです。
let card;
let angle = 0;
let centerX;
let centerY;
let offscreenCanvas; // オフスクリーンキャンバス
let isCardRotation = false; // カードが回転しているかどうか
let isCircleDrawing = false; // 円が回転しているかどうか
let isTriangleDrawing = false; // 三角形が回転しているかどうか
function preload() {
card = loadImage('images/card.png');
}
function setup() {
createCanvas(400, 300);
angleMode(DEGREES);
imageMode(CENTER);
centerX = width / 2;
centerY = height / 2;
// オフスクリーンキャンバスをカードのイメージサイズで作成
offscreenCanvas = createGraphics(card.width, card.height);
// [左に丸を描く]ボタン
const circleButton = setButton('左に丸を描く', {
x: 20,
y: 320
});
circleButton.mousePressed(() => {
// 円を描画
isCircleDrawing = true;
});
// [カードを180度回転]ボタン
const rotateCardButton = setButton('カードを180度回転', {
x: 160,
y: 320
});
rotateCardButton.mousePressed(() => {
// カードを回転
isCardRotation = true;
});
// [左に三角形を描く]ボタン
const triangleButton = setButton('左に三角形を描く', {
x: 300,
y: 320
});
triangleButton.mousePressed(() => {
// 三角を描画
isTriangleDrawing = true;
});
}
function draw() {
background(220);
translate(centerX, centerY);
// [カードを180度回転]ボタンが押されたら
if (isCardRotation) {
rotate(angle);
if (angle >= 180) {
angle = 180;
}
else {
angle++;
}
}
// オフスクリーンキャンバスにカードを描画
offscreenCanvas.image(card, 0, 0);
// [左に丸を描く]ボタンが押されたら
if (isCircleDrawing) {
// オフスクリーンキャンバスに円を描画
drawCircle('left');
}
// [左に三角形を描く]ボタンが押されたら
if (isTriangleDrawing) {
// オフスクリーンキャンバスに三角を描画
// カードが180度回転した状態で描画するので、三角形の位置は"右"にする
drawTriangle('right');
}
// ここまで描いてきたオフスクリーンキャンバスをキャンバスに描画
image(offscreenCanvas, 0, 0);
}
// オフスクリーンキャンバスに円を描画
function drawCircle(pos) {
offscreenCanvas.fill(color(124, 176, 207));
let x;
if (pos === 'right') {
x = 240;
}
else if (pos === 'left') {
x = 50;
}
offscreenCanvas.ellipse(x, 100, 50);
}
// オフスクリーンキャンバスに三角を描画
function drawTriangle(pos) {
offscreenCanvas.fill(color(243, 241, 107));
let x;
if (pos === 'right') {
x = 240
}
else if (pos === 'left') {
x = 50;
}
const points = getTrianglePoinsts(x, offscreenCanvas.height / 2, 50);
offscreenCanvas.triangle(points[0][0], points[0][1], points[1][0], points[1][1], points[2][0], points[2][1]);
}
// 中心位置と半径から正三角形の頂点を計算して返す
function getTrianglePoinsts(cX, cY, radius) {
let result = [];
// カードが180度回転した状態で描画するので、三角形の頂点を真下向きにする
let ang = 90;
for (let i = 0; i < 3; i++) {
const cosValue = cos(ang);
const sinValue = sin(ang);
const x = cX + cosValue * radius;
const y = cY + sinValue * radius;
result.push([int(x), int(y)]);
ang += 120;
}
return result;
}
function setButton(label, pos) {
const button = createButton(label);
button.size(100, 50);
button.position(pos.x, pos.y);
return button;
}3つのボタンはどのタイミングでもクリックできます。三角はオフスクリーンキャンバスに描いているので、カードの回転といっしょに回転します。
