プログラミング はじめの一歩 JavaScript + p5.js編
35：家から学校までの道　どれが一番早く着くかな(ダイクストラ法)

この記事の詳しい内容には毎日新聞の「家から学校までの道　どれが一番早く着くかな」ページから有料記事に進むことで読めます。

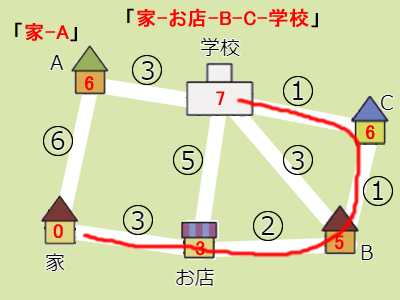
概要

下図は、学校周辺の地図を示しています。丸の中の数は、その道を通ったときにかかる分数です。たとえば家とお店の間は３分かかることが分かります。

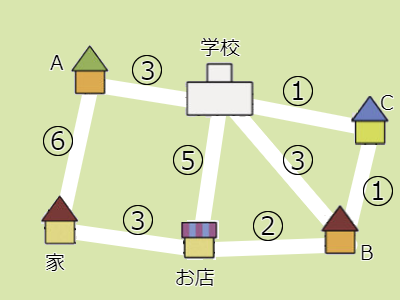
ここで問題です。家から学校まで移動するとき、

• 家からお店まで最も早い道を選ぶ
• お店から学校まで最も早い道を選ぶ

ことを条件とした場合、どのルートを取るのが一番早いでしょうか？　同じ道は何度も通ることができます。

手で書いて考えてみる

示されている条件通りに、地道に手で書いて考えてみます。

まず、「家からお店まで最も早い道を選ぶ」ということなので、家からお店までは、家 – A – 学校 – お店 (6+3+5=14分かかる)というルートではなく、家 – お店(3分かかる)というルートを選びます。

次の条件は「お店から学校まで最も早い道を選ぶ」です。お店 – 学校は5分、お店 – B – 学校も5分(2+3)ですが、お店 – B – C – 学校は4分(2+1+1)なので、これが早く着くルートになります。

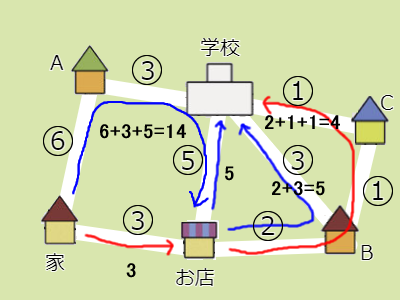
したがってお題の答えは、家 – お店 – B – C – 学校 のルートです。3+2+1+1=7分で到着します。

論理を考える

このお題の答えを求めること自体は難しくありませんが、これをプログラミングで考えるとなると、それは相当高いハードルです。

ざっと考えるだけでも、まずたどれるルートをどのように設定するかを考える必要があります。これは、たとえば、家からはお店やAには進めますが、BやCには直接は進めないことをプログラミングでどう表すか、ということです。また家から出て、次の地点に着いたときにはそのたびにかかった分数を足していく必要があり、その合計分数をルート別にメモしておいて比べる必要があります。

さらに言えば、このお題の地図だけでなく、ほかの場合にも適用できるプログラムにしたいという希望もあります。

とは言えこの難題に１人で取り組む必要はありません。この問題は「最短経路問題」という用語で、優れた先人たちによってすでに解き方が公開されています。

最短経路問題
グラフ理論における最短経路問題（さいたんけいろもんだい、英: shortest path problem）とは、重み付きグラフの与えられた2つのノード間を結ぶ経路の中で、重みが最小の経路を求める最適化問題である。

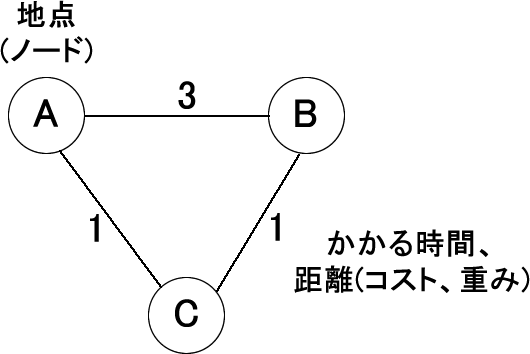
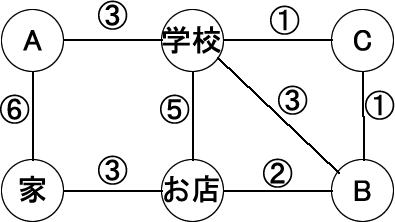
この説明文はずいぶん難しく書かれていますが、分かりやすくいうと、ノードとは地点を言っており、スタート地点や経由地点、ゴール地点などがあります。それを結ぶ線はエッジと呼ばれ、エッジには重みが付けられます。これはあるノードからあるノードへの行きやすさ(または行きにくさ)、つまり移動にかかる時間や距離と考えることができます。

下図のAからBに移動するとき、一見すると「A – B」というルートが早そうに見えますが、重みが3(3分かかる)です。一方、「A – C – B」はCを経由するので時間がかかりそうに思えますが、重みが2(1 + 1)なので、このルートが最短と考えられます。このように、ノードやエッジのつながりで表された構造はグラフと呼ばれます。前述した、家からはお店やAには進めるがBやCには直接は進めないことや、移動にかかる時間はこのグラフのデータ構造で表すことができます。

最短経路問題を解く方法には、有名なものに「ダイクストラ法」や「ベルマン-フォード法」があります。「ダイクストラ法」は重みが正の数の場合に使用できるのに対し、「ベルマン-フォード法」は重みが負の数の場合でも使用できるという違いがあります。今回のお題は重みが全部正なので、「ダイクストラ法」が使用できます。

ダイクストラ法

「ダイクストラ法」の優れた点は、考えられるすべての経路を計算しなくても、効率的に最短の経路が探索できることにあると言われます。次の手順は「ダイクストラ法」で使われる計算の考え方(アルゴリズム)です。YouTubeで公開されている「グラフ理論(5)(ダイクストラのアルゴリズム)」を参考にしています。

1. 始点に0を書き込む(ほかの地点は無限大にする)
2. 未確定の地点の中から最も小さい値を持つ地点を１つ選び、その値を確定させる。ルートも記録する
3. ２で確定した地点から直接つながっていてかつ未確定な地点に対し、かかる時間を計算し、書き込まれている値より小さければ更新する
4. すべての地点で確定していれば終了する。そうでなければ２に戻る

ではこの手順にしたがって、お題の最短距離を１つずつ探っていきましょう。

お題をダイクストラ法で１つずつ探る

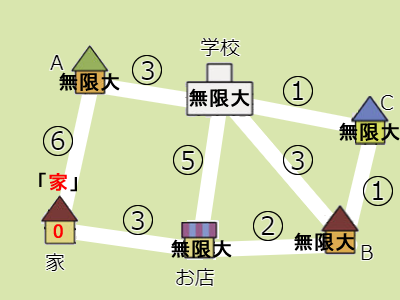
1. 手順1では、始点に0を書き込むということなので、家に0を書き込みます。またほかの地点は無限大にします。
   
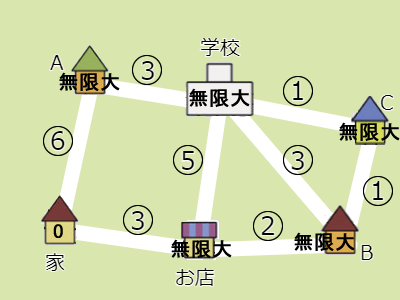
2. 手順２は「未確定の地点の中から最も小さい値を持つ地点を１つ選び、その値を確定させる」です。確定した地点はまだなく、最も小さな値を持つ地点は家(0)です。これを確定させます(赤字は確定を示します)。またルートも記録します。ルートは「家」のみです(スタート地点に立った状態)。
   
3. 次の手順３は「２で確定した地点から直接つながっていてかつ未確定な地点に対し、かかる時間を計算し、書き込まれている値より小さければ更新する」です。手順２で確定した地点(家)から直接つながっていてかつ未確定な地点というのは、お店とAです。家からかかる時間は、お店までが3分で、Aまでが6分です。書き込まれている無限大よりどちらも小さいので、これらを更新します。
   
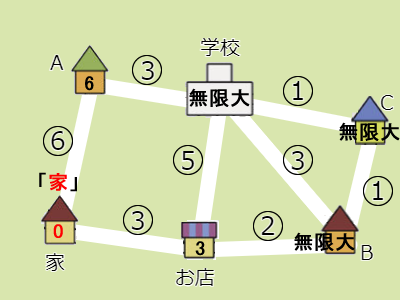
4. 次の手順４は「すべての地点で確定していれば終了する。そうでなければ２に戻る」です。まだ始めたばかりで確定していない地点はたくさんあるので、手順２に戻ります。
5. 「未確定の地点の中から最も小さい値を持つ地点」はお店(3)なので、これを確定させます。ルートは「家 – お店」になります。
   
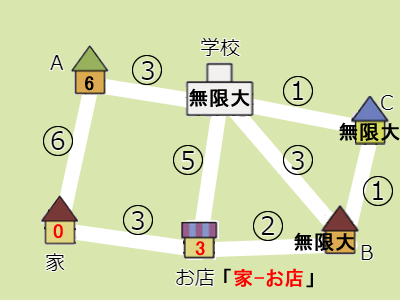
6. 「２で確定した地点」はお店で、そこ「から直接つながっていてかつ未確定な地点」は学校とBです。家からかかる時間は、学校までが8分(3+5)で、Bまでが5分(3+2)です。書き込まれている値無限大より小さいので、更新します。
   
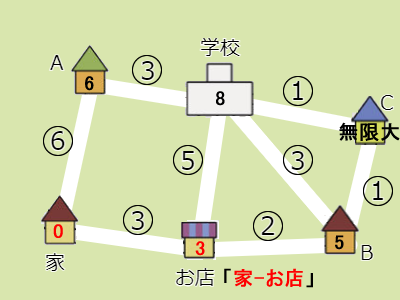
7. 未確定の地点はまだまだ残っているので、手順２に戻ります。
8. 未確定の地点はA(6)、B(5)、C(無限大)、学校(8)です。この中で最も小さな値を持つ地点はBなので、これを確定させます。ルートは「家 – お店 – B」となります。
   
9. Bから直接つながっていて未確定なのは、Cと学校です。家からCまでかかる時間は6分(3+2+1)で、学校までは8分(3+2+3)です。Cの6は無限大より小さいので値を更新します。学校はすでに8なので更新しません。ここまでで無限大がなくなりました。
   
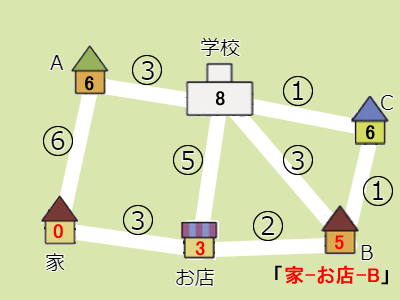
10. かなり進んで来ましたが、まだすべての地点で確定していないので、手順２に戻ります。
11. 「未確定の地点の中から最も小さい値を持つ地点を１つ選び、その値を確定させ」ます。しかし今、最も小さな値を持つ地点は、A(6)とC(6)の２つです。選べるのは１つだけなので、まずAを確定させます(どれを先に選んでも構いません)。ルートは「家 – A」となります。これは、ここまでつないできたルートとは別のルートです。
    
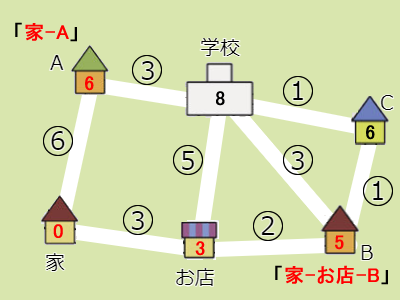
12. 確定させたAから直接つながっていてかつ未確定な地点は学校で、かかる時間は9分(6+3)です。これは、すでに書き込まれている8よりも大きいので更新しません。
13. Aを確定させたので、Aと同じ6のCを確定させます。ルートは「家 – お店- B – C」となります。
    
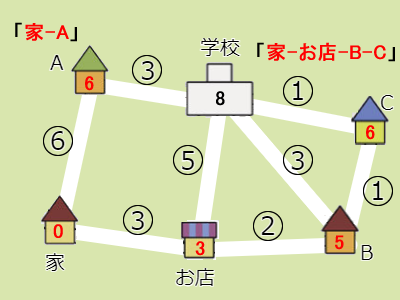
14. 確定させたCから直接つながっていてかつ未確定な地点は学校で、かかる時間は7分(3+2+1+1)です。これは、すでに書き込まれている8よりも小さいので更新します。
    
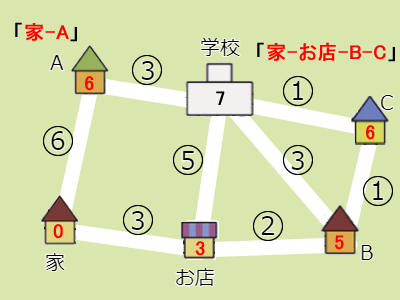
15. 学校だけ確定していないので、手順２に戻ります。
16. 未確定の地点の中の最も小さい値を持つ地点は学校なので、その値を確定させます。ルートは「家 – お店- B – C – 学校」です。
    
17. 確定させた学校から直接つながっている未確定な地点はありません。
18. すべての地点で確定したので終了します。

書籍やほかのページなら省略しそうな細部も見たので、相当長くなりましたが、前の「手で書いて考えてみる」と同じ結果が得られました。

「ダイクストラ法」によるプログラムコード

では、お題を「ダイクストラ法」で解決するプログラムのコードを見ていきましょう。

グラフを表す

JavaScriptのコードで表したいのは、下図のグラフです。

この構造を表すには、いくつかの方法が考えられます。

たとえば次の方法は、JavaScriptの汎用オブジェクト(Objectオブジェクト)を使った連想配列と呼ばれる構造による方法です。この方法では、キー:値 の形式でデータを保持するので、ノード間の関係性が分かりやすくなります。たとえば、house: { shop: 3, A: 6 } というキー:値 の形式で、houseノードは、shopとAに接続し、それぞれ3と6のコストを持つということが表せます。

let graphData = {
  house: { shop: 3, A: 6 },
  shop: { house: 3, school: 5, B: 2 },
  school: { A: 3, shop: 5, B: 3, C: 1 },
  A: { house: 6, school: 3 },
  B: { shop: 2, school: 3, C: 1 },
  C: { school: 1, B: 1 }
}

また２次元配列でも表すことができます。具体的なノード名がないので分かりづらくはありますが、配列の中に数値が並んでいるだけなので、データへのアクセスが容易です。

let graphData = [
    [0, 6, 0, 0, 0, 3],
    [6, 0, 3, 0, 0, 0],
    [0, 3, 0, 1, 3, 5],
    [0, 0, 1, 0, 1, 0],
    [0, 0, 3, 1, 0, 2],
    [3, 0, 5, 0, 2, 0]
];

この２次元配列は、下図に示すエクセルの表に置き換えることができます。ポイントは、横の行(2,3,4,5,6,7)が接続元のノードに対応し、縦の列の接続先(B,C,D,E,F,G)に接続することを表す、という点です。

たとえばschool – A はコスト3なので、セルC4は3です。0はつながっていないことを表します。また自分から自分への接続は0と考えることができるので、home – home や A – A は0です。

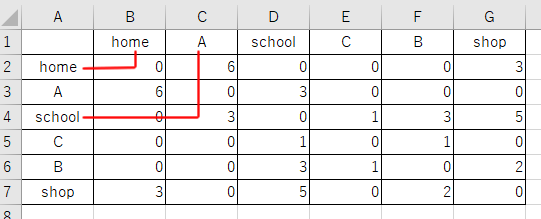
２次元配列を使った方法は、数値の要素の並びを間違えない限り、連想配列の方法より数値の取り出しが少し簡単なので、グラフの構造は２次元配列で表すことにします。

では、前述した手順に沿って、プログラムのコードを見ていきましょう。

手順１までのコード

graphDataという名前の２次元配列を作成した後、手順１までのコードは次のように記述できます。

...
// ノードの名前。家から右回り
let nodeNames = ['home', 'A', 'school', 'C', 'B', 'shop'];
// ノードを表すMapオブジェクトを入れる配列
let nodeMaps = [];
let startNode;
let goalNode; // ゴールのノード

function setup() {
        noCanvas();
        // ノードのデータ分だけMapオブジェクトを作成し、配列に追加する
        for (let i = 0; i < graphData.length; i++) {
            const map = new Map();
            map.set('name', nodeNames[i]); // 名前
            map.set('nodeData', graphData[i]); // 値はノードの情報の配列
            map.set('cost', Number.MAX_VALUE); // 非常に大きな値に設定
            map.set('visited', false); // 訪問(確定)したかどうか
            map.set('parent', null); // 親ノード(このノードへの接続元)
            nodeMaps.push(map);
        }

        startNode = nodeMaps[0]; // スタートは家
        goalNode = nodeMaps[2]; // ゴールは学校

        // スタートノードのコストを0にする
        // => (手順１) 始点に0を書き込む)(ほかの地点は無限大にする)
        for (let i = 0; i < nodeMaps.length; i++) {
            const map = nodeMaps[i];
            if (map === startNode) {
                map.set('cost', 0);
            }
        }

手順１は「始点に0を書き込む(ほかの地点は無限大にする)」です。上記コードでは、「ほかの地点は無限大にする」を、１つめのforループのmap.set(‘cost’, Number.MAX_VALUE);で行っています。これにより作成されるMapオブジェクトのcost値は全部非常に大きな数値になります。そして、２つめのforループで、starNode値と比較してスタートノードのcost値を0に設定しています。

nodeNames配列は、graphData２次元配列のデータとの関連付けに使用するので、文字列の並び順をgraphDataのデータの並び順と同じにする必要があります。graphDataのデータの順番は、前のエクセルの表の通り、「家」から右回りに進んだ順番(home, A, school,C,B,shop)です。

Mapオブジェクトに設定しているvisitedはそのノードを確定したかどうかに、parentはそのノードの接続元への参照に使用します。

変数startNodeにはスタート地点に当たるノードを、goalNodeにはゴール地点に当たるノードを指定します。お題の場合、スタート地点は「家」なのでnodeMaps[0]を、ゴール地点は「学校」なのでnodeMaps[2]を割り当てていますが、これは自由に変更できる仕様にします。

手順２までのコード

手順２は「未確定の地点の中から最も小さい値を持つ地点を１つ選び、その値を確定させる。ルートも記録する」です。「未確定の地点の中から最も小さい値を持つ地点を１つ選ぶ」コードは次のように記述できます。

// 未訪問のノードのうち、コストが最小のものを調べて返す
function getMinNode() {
    // 未訪問のノードを調べる
    const unvisitedNodes = nodeMaps.filter((map) => {
        return !map.get('visited');
    });
    // 未訪問のノードのうちコストが最小のものを調べる
    const minNode = unvisitedNodes.reduce((a, b) => {
        if (a.get('cost') <= b.get('cost')) {
            return a;
        }
        else {
            return b;
        }
    });
    return minNode;
}

ここでは配列のfilter()とreduce()メソッドを使って、欲しいノードを求めています。filter()は「与えられた関数によって実装されたテストに合格したすべての配列からなる新しい配列を生成する」ので、ここでは、nodeMaps配列に入っているMapオブジェクトに対して、visitedがfalseであるものを集めた配列unvisitedNodesを作成しています。

reduce()は「配列の各要素に対して (引数で与えられた) reducer 関数を実行して、単一の出力値を生成する」ので、ここではunvisitedNodes配列に含まれる(visitedがfalseである)Mapオブジェクトaとbのコスト値の大小を比べ、最小のコスト値を持つMapオブジェクトをminNodeとして確定させています。

次のコードでこの関数を呼び出し、返された結果を出力すると、

const node = getMinNode();
print(node);

次のhomeノードが表示されます。

プログラムの開始時点では、全部のMapオブジェクトのvisitedはfalseなので、unvisitedNodes配列にはすべてのノードが含まれることになります。そしてcost値はhomeだけが0で、ほかのノードは全部Number.MAX_VALUEなので、homeが返されます。

コスト値を確定させるのは、(一連の作業の後)次のコードで行います。

// (手順２) その値を確定させる
closestNode.set('visited', true);

またルートの記録は(一連の作業の途中)次のコードで行います。

// (手順２) ルートも記録する
targetMap.set('parent', closestNode);

手順３までのコード

手順３は「手順２で確定した地点から直接つながっていてかつ未確定な地点に対し、かかる時間を計算し、書き込まれている値より小さければ更新する」です。

「手順２で確定した地点」というのはgetMinNode()関数が返すノードのMapオブジェクトです。これが「直接つながってい」る地点は、getMinNode()関数が返したMapオブジェクトのnodeData値の配列で分かります。

具体的に、最初のgetMinNode()への呼び出しで見ていくと、このときにはhomeノードが返されます。このMapオブジェクトのnodeDataは[0, 6, 0, 0, 0, 3]です。直接つながっているノードは0でない地点なので、6の「A」と3の「お店」だと分かります(配列の並びは、家、A、学校、C、B、お店の順です)。このノードに対してコストの大小を調べ、必要ならその値を更新します。

こうした作業を行うコードは次のように記述できます。

// (手順２) 未確定の地点の中から最も小さい値を持つ地点を１つ選ぶ
const closestNode = getMinNode();
// ノードの情報。これは配列
let costsArray = closestNode.get('nodeData');
// 配列の要素(cost)とインデックス番号を使って、
costsArray.forEach((cost, index) => {
    // コストが正の場合に
    if (cost > 0) {
        // 対象となるノード
        const targetMap = nodeMaps[index];
        // (手順３) ２で確定した地点から直接つながっていてかつ未確定な地点に対し、かかる時間を計算し、
        // 書き込まれている値より小さければ更新する
        if (targetMap.get('cost') > cost + closestNode.get('cost')) {
            targetMap.set('cost', cost + closestNode.get('cost'));
            // (手順２) ルートも記録する => 対象Mapの親ノードを記録しておくと、後でたどることができる
            targetMap.set('parent', closestNode);
        }
    }
});// (手順２) その値を確定させる
closestNode.set('visited', true);

上記コードには、手順２のルートの記録とノードの確定も含まれています。

手順４までのコード

手順４は「すべての地点で確定していれば終了する。そうでなければ２に戻る」です。

「すべての地点で確定してい」るとは、全部のMapオブジェクトのvisitedがtrueになっているということです。そうでなければ、手順２のgetMinNode()の呼び出しから繰り返します。

コードは次のように記述できます。ここでは変数loopを設定し、これがtrueである間、whileループを繰り返します。

let loop = true; // loop変数がtrueの間繰り返す
while (loop) {
    // (手順２) 未確定の地点の中から最も小さい値を持つ地点を１つ選ぶ
    const closestNode = getMinNode();
    // ノードの情報。これは配列
    let costsArray = closestNode.get('nodeData');
    // 配列の要素(cost)とインデックス番号を使って、
    costsArray.forEach((cost, index) => {
        // コストが正の場合に
        if (cost > 0) {
            // 対象となるノード
            const targetMap = nodeMaps[index];
            // (手順３) ２で確定した地点から直接つながっていてかつ未確定な地点に対し、かかる時間を計算し、
            // 書き込まれている値より小さければ更新する
            if (targetMap.get('cost') > cost + closestNode.get('cost')) {
                targetMap.set('cost', cost + closestNode.get('cost'));
                // (手順２) ルートも記録する => 対象Mapの親ノードを記録しておくと、後でたどることができる
                targetMap.set('parent', closestNode);
            }
        }
    });
    // (手順２) その値を確定させる
    closestNode.set('visited', true);

    // (手順４) すべての地点で確定していれば終了する。そうでなければ２に戻る
    let count = 0;
    nodeMaps.forEach((node) => {
        if (node.get('visited') === true) {
            count++;
            if (count === graphData.length - 1) {
                loop = false;
            }
        }
    });
}

whileループは、visitedがtrueであるMapオブジェクトの数を数えるcount変数がグラフのgraphData配列の要素数-1になったタイミングで、loop変数をfalseにすることで停止します。

結果の収集

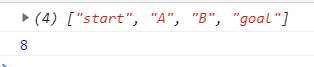
ここまで見てきたコードを実行し、最後にnodeMapsを出力すると、下図の結果が得られます。

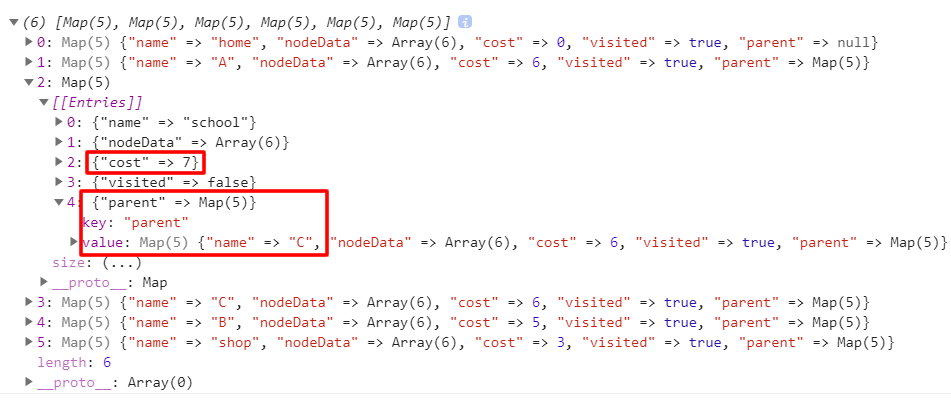
ゴール地点である「学校」を表すschoolノードのcost値を見ると、7であることが分かります(上の赤枠内)。これは「手で書いて考えてみる」で出した答え、3 + 2 + 1 + 1 = 7分 と一致する値です。

またschoolのparentはCノードであることも分かります(下の赤枠)。各ノードのMapオブジェクトはparentがnullでない限り、接続元を持っています。これをゴール地点からたどると、スタート地点からゴール地点までの最短経路が分かります。

このコードは次のように記述できます。

// 親ノードのリスト(各Mapの接続元を集める)
let parents = [goalNode]; // 最後はゴールノード
let parent = parents[0].get('parent'); // ゴールノードの親ノード
while (parent) {
    // parentistの最初の要素の親ノード
    parent = parents[0].get('parent');
    if (parent !== null) {
        // parentistの先頭に追加する。経路が定まる
        parents.unshift(parent);
    }
}
let routeList = [];
parents.forEach((parent) => {
    routeList.push(parent.get('name'))
});

print(routeList); // 経路が分かる
print(goalNode.get('cost')); // ゴールノードまでのコスト

全コード

以下は「ダイクストラ法」を使ったプログラムに使用できる全コードです。

// ６つのノードのつながりとコストに関する情報
// 行、列ともに、家 -> A -> 学校 -> C -> B -> お店 の順番
// 家から右回り。0は接続がないことを表す
let graphData = [
    [0, 6, 0, 0, 0, 3], // 家：家(0)、A(6),学校(0)、C(0),B(0),お店(3)
    [6, 0, 3, 0, 0, 0], // A：家(6),A(0)、学校(3),C(0),B(0)、お店(0)
    [0, 3, 0, 1, 3, 5],
    [0, 0, 1, 0, 1, 0],
    [0, 0, 3, 1, 0, 2],
    [3, 0, 5, 0, 2, 0]
];
// ノードの名前。家から右回り
let nodeNames = ['home', 'A', 'school', 'C', 'B', 'shop'];
// ノードを表すMapオブジェクトを入れる配列
let nodeMaps = [];
let startNode;
let goalNode; // ゴールのノード

function setup() {
    noCanvas();
    // ノードのデータ分だけMapオブジェクトを作成し、配列に追加する
    for (let i = 0; i < graphData.length; i++) {
        const map = new Map();
        map.set('name', nodeNames[i]); // 名前
        map.set('nodeData', graphData[i]); // 値はノードの情報の配列
        map.set('cost', Number.MAX_VALUE); // 非常に大きな値に設定
        map.set('visited', false); // 訪問(確定)したかどうか
        map.set('parent', null); // 親ノード(このノードへの接続元)
        nodeMaps.push(map);
    }

    startNode = nodeMaps[0]; // スタートは家
    goalNode = nodeMaps[2]; // ゴールは学校

    // スタートノードのコストを0にする
    // => (手順１) 始点に0を書き込む)(ほかの地点は無限大にする)
    for (let i = 0; i < nodeMaps.length; i++) {
        const map = nodeMaps[i];
        if (map === startNode) {
            map.set('cost', 0);
        }
    }

    let loop = true; // loop変数がtrueの間繰り返す
    while (loop) {
        // (手順２) 未確定の地点の中から最も小さい値を持つ地点を１つ選ぶ
        const closestNode = getMinNode();
        // ノードの情報。これは配列
        let costsArray = closestNode.get('nodeData');
        // 配列の要素(cost)とインデックス番号を使って、
        costsArray.forEach((cost, index) => {
            // コストが正の場合に
            if (cost > 0) {
                // 対象となるノード
                const targetMap = nodeMaps[index];
                // (手順３) ２で確定した地点から直接つながっていてかつ未確定な地点に対し、かかる時間を計算し、
                // 書き込まれている値より小さければ更新する
                if (targetMap.get('cost') > cost + closestNode.get('cost')) {
                    targetMap.set('cost', cost + closestNode.get('cost'));
                    // (手順２) ルートも記録する => 対象Mapの親ノードを記録しておくと、後でたどることができる
                    targetMap.set('parent', closestNode);
                }
            }
        });
        // (手順２) その値を確定させる
        closestNode.set('visited', true);

        // (手順４) すべての地点で確定していれば終了する。そうでなければ２に戻る
        let count = 0;
        nodeMaps.forEach((node) => {
            if (node.get('visited') === true) {
                count++;
                if (count === graphData.length - 1) {
                    loop = false;
                }
            }
        });
    }

    // 親ノードのリスト(各Mapの接続元を集める)
    let parents = [goalNode]; // 最後はゴールノード
    let parent = parents[0].get('parent'); // ゴールノードの親ノード
    while (parent) {
        // parentistの最初の要素の親ノード
        parent = parents[0].get('parent');
        if (parent !== null) {
            // parentistの先頭に追加する。経路が定まる
            parents.unshift(parent);
        }
    }
    let routeList = [];
    parents.forEach((parent) => {
        routeList.push(parent.get('name'))
    });

    print(routeList); // 経路が分かる
    print(goalNode.get('cost')); // ゴールノードまでのコスト

}

// 未訪問のノードのうち、コストが最小のものを調べて返す
function getMinNode() {
    // 未訪問のノードを調べる
    const unvisitedNodes = nodeMaps.filter((map) => {
        return !map.get('visited');
    });
    // 未訪問のノードのうちコストが最小のものを調べる
    const minNode = unvisitedNodes.reduce((a, b) => {
        if (a.get('cost') <= b.get('cost')) {
            return a;
        }
        else {
            return b;
        }
    });
    return minNode;
}

結果は下図のように出力されます。

別のグラフでテスト

YouTubeで公開されている「グラフ理論(5)(ダイクストラのアルゴリズム)」の例で取り上げられている下図のグラフでテストしてみましょう。

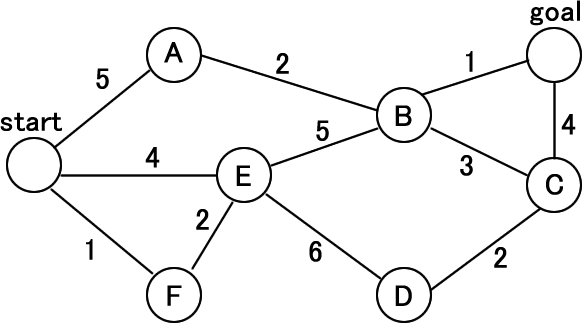
前述したプログラミングコードに適用するために、グラフの２次元配列やノード名の配列、スタートノードやゴールノードの変数を設定します。

let graphData = [
    [0, 5, 0, 0, 0, 0, 4, 1],
    [5, 0, 2, 0, 0, 0, 0, 0],
    [0, 2, 0, 1, 3, 0, 5, 0],
    [0, 0, 1, 0, 4, 0, 0, 0],
    [0, 0, 3, 4, 0, 2, 0, 0],
    [0, 0, 0, 0, 2, 0, 6, 0],
    [4, 0, 5, 0, 0, 6, 0, 2],
    [1, 0, 0, 0, 0, 0, 2, 0]
];
// ノードの名前。startから右回り
let nodeNames = ['start', 'A', 'B', 'goal', 'C', 'D', 'E', 'F'];

...

startNode = nodeMaps[0]; // スタートはstart
goalNode = nodeMaps[3]; // ゴールはgoal

下図はこの実行結果です。

最短経路を示すアプリ

では最後に、お題の学校周辺の地図を題材に、スタート地点とゴール地点を選び、その間の最短経路を示すアプリを紹介しておきます。

以下はアプリの全コードです。

// 視覚化

// ６つのノードのつながりとコストに関する情報
// 行、列ともに、家 -> A -> 学校 -> C -> B -> お店 の順番
// 家から右回り。0は接続がないことを表す
let graphData = [
    [0, 6, 0, 0, 0, 3], // 家：家(0)、A(6),学校(0)、C(0),B(0),お店(3)
    [6, 0, 3, 0, 0, 0], // A：家(6),A(0)、学校(3),C(0),B(0)、お店(0)
    [0, 3, 0, 1, 3, 5],
    [0, 0, 1, 0, 1, 0],
    [0, 0, 3, 1, 0, 2],
    [3, 0, 5, 0, 2, 0]
];
// ノードの名前。家から右回り
let nodeNames = ['home', 'A', 'school', 'C', 'B', 'shop'];
// ノードを表すMapオブジェクトを入れる配列
let nodeMaps = [];

// 描画関連
// 描画物の配置に使用するベース位置。これを基本にほかのものの描画位置を決める
let baseX = 60,
    baseY = 220;
// 赤線ルートを表す線の描画に使用する位置
let centerPos = [{
    x: baseX,
    y: baseY + 10
}, {
    x: baseX + 30,
    y: baseY - 140
}, {
    x: baseX + 160,
    y: baseY - 120
}, {
    x: baseX + 310,
    y: baseY - 90
}, {
    x: baseX + 280,
    y: baseY + +20
}, {
    x: baseX + 140,
    y: baseY + 30
}];
let nodeImages = []; // ノードを表すイメージを入れる配列
let lines = []; // 赤線ルートを表す線の座標を入れる配列
let isDrawPath = false; // trueのとき赤線ルートを描画する

// イメージを読み込み、nodeImages配列に追加する
function preload() {
    for (let i = 0; i < nodeNames.length; i++) {
        const img = loadImage('images/' + nodeNames[i] + '.png');
        nodeImages.push(img);
    }
}

function setup() {
    createCanvas(400, 300);
    background(219, 229, 174);
    // イメージのセンターにもとづいて描画するモード
    imageMode(CENTER);

    // スタート場所を設定するselect要素
    // nodeNamesと同じ順番
    const startSel = createSelect();
    startSel.position(50, 310);
    startSel.option('家', 0);
    startSel.option('A', 1);
    startSel.option('学校', 2);
    startSel.option('C', 3);
    startSel.option('B', 4);
    startSel.option('お店', 5);
    startSel.selected(0);
    // 文字を描画する
    const p1 = createP('から');
    p1.position(110, 293);
    // 終了場所を設定するselect要素
    const endSel = createSelect();
    endSel.position(150, 310);
    endSel.option('家', 0);
    endSel.option('A', 1);
    endSel.option('学校', 2);
    endSel.option('C', 3);
    endSel.option('B', 4);
    endSel.option('お店', 5);
    endSel.selected(2);
    // 文字を描画する
    const p2 = createP('まで');
    p2.position(210, 293);
    // [GO]ボタン
    const goButton = setButton('GO', {
        x: 270,
        y: 310
    });
    // マウスプレスで、探索開始
    goButton.mousePressed(() => {
        // nodeMapsとlines配列を初期化
        nodeMaps = [];
        // ノードのデータ分だけMapオブジェクトを作成し、配列に追加する
        for (let i = 0; i < graphData.length; i++) {
            const map = new Map();
            map.set('name', nodeNames[i]); // 名前
            map.set('nodeData', graphData[i]); // 値はノードの情報の配列
            map.set('cost', Number.MAX_VALUE); // 非常に大きな値に設定
            map.set('visited', false); // 訪問(確定)したかどうか
            map.set('parent', null); // 親ノード(このノードへの接続元)
            map.set('centerPos', centerPos[i]);
            nodeMaps.push(map);
        }

        lines = [];
        isDrawPath = false;
        // 2つのselect要素の値を調べdijkstra()関数に渡してこれを呼び出す。
        const startIndex = startSel.value();
        const endIndex = endSel.value();
        // dijkstraはダイクストラ
        const resultArray = dijkstra(nodeMaps[startIndex], nodeMaps[endIndex]);
        // 結果の配列に含まれるMapオブジェクトのcenterPosを使って、赤線を描く
        for (let i = 0; i < resultArray.length; i++) {
            const pos = resultArray[i].get('centerPos');
            lines.push(pos);
        }
        isDrawPath = true;
    });
}

function dijkstra(startMap, endMap) {
    startNode = startMap;
    goalNode = endMap;
    // スタートノードのコストを0にする
    // => (手順１) 始点に0を書き込む)(ほかの地点は無限大にする)
    for (let i = 0; i < nodeMaps.length; i++) {
        const map = nodeMaps[i];
        if (map === startNode) {
            map.set('cost', 0);
        }
    }

    let loop = true; // loop変数がtrueの間繰り返す
    while (loop) {
        // (手順２) 未確定の地点の中から最も小さい値を持つ地点を１つ選ぶ
        let closestNode = getMinNode();
        // ノードの情報。これは配列
        let costsArray = closestNode.get('nodeData');
        // 配列の要素(cost)とインデックス番号を使って、
        costsArray.forEach((cost, index) => {
            // コストが正の場合に
            if (cost > 0) {
                // 対象となるノード
                const targetMap = nodeMaps[index];
                // (手順３) ２で確定した地点から直接つながっていてかつ未確定な地点に対し、かかる時間を計算し、
                // 書き込まれている値より小さければ更新する
                if (targetMap.get('cost') > cost + closestNode.get('cost')) {
                    targetMap.set('cost', cost + closestNode.get('cost'));
                    // (手順２) ルートも記録する => 対象Mapの親ノードを記録しておくと、後でたどることができる
                    targetMap.set('parent', closestNode);
                }
            }
        });
        // (手順２) その値を確定させる
        closestNode.set('visited', true);

        // (手順４) すべての地点で確定していれば終了する。そうでなければ２に戻る
        let count = 0;
        nodeMaps.forEach((node) => {
            if (node.get('visited') === true) {
                count++;
                if (count === graphData.length - 1) {
                    loop = false;
                }
            }
        });
    }
    // 親ノードのリスト(各Mapの接続元を集める)
    let parents = [goalNode]; // 最後はゴールノード
    let parent = parents[0].get('parent'); // ゴールノードの親ノード
    while (parent) {
        // parentistの最初の要素の親ノード
        parent = parents[0].get('parent');
        if (parent !== null) {
            // parentistの先頭に追加する。経路が定まる
            parents.unshift(parent);
        }
    }
    let routeList = [];
    parents.forEach((parent) => {
        routeList.push(parent.get('name'))
    });
    print(routeList); // 経路が分かる
    print(goalNode.get('cost')); // ゴールノードまでのコスト
    return parents;
}

// 描画
function draw() {
    background(219, 229, 174);
    // 道を描画
    stroke(255);
    strokeWeight(15);
    drawRoad();

    // かかる分数を描画
    strokeWeight(1);
    textSize(25);
    drawMin();
    // 建物(ノード)とその名前を描画
    drawNodeImage();
    drawNodeName();
    // line配列が持っている値を使って赤線を描く
    if (isDrawPath) {
        strokeWeight(5);
        stroke(255, 0, 0);
        for (let i = 0; i < lines.length - 1; i++) {
            line(lines[i].x, lines[i].y, lines[i + 1].x, lines[i + 1].y)
        }
        stroke(255);
    }
}

// 道を描画
function drawRoad() {
    // 家 - 店の道
    line(baseX, baseY + 10, baseX + 140, baseY + 30);
    // 家 - Aの道
    line(baseX, baseY + 10, baseX + 35, baseY - 150);
    // A - 学校の道
    line(baseX + 35, baseY - 135, baseX + 160, baseY - 115);
    // 店 - 学校の道
    line(baseX + 140, baseY + 20, baseX + 160, baseY - 115);
    // 店 - Bの道
    line(baseX + 140, baseY + 30, baseX + 280, baseY + 25);
    // 学校 - Bの道
    line(baseX + 170, baseY - 115, baseX + 290, baseY + 25);
    // C - Bの道
    line(baseX + 315, baseY - 100, baseX + 285, baseY + 25);
    // C - 学校の道
    line(baseX + 315, baseY - 90, baseX + 160, baseY - 120);
}

// かかる分数の描画
function drawMin() {
    // 家 - 店
    text('3', baseX + 70, baseY + 10);
    // 家 - A
    text('6', baseX - 10, baseY - 70);
    // A - 学校
    text('3', baseX + 80, baseY - 140);
    // 店 - 学校
    text('5', baseX + 120, baseY - 50);
    // 店 - B
    text('2', baseX + 200, baseY + 15);
    // 学校 - B
    text('3', baseX + 230, baseY - 50);
    // C - B
    text('1', baseX + 310, baseY - 20);
    // C - 学校
    text('1', baseX + 230, baseY - 120);
}

// ノード(地点の建物のイメージ)の描画
function drawNodeImage() {
    // 家
    image(nodeImages[0], baseX, baseY);
    // お店
    image(nodeImages[1], baseX + 140, baseY + 20);
    // 学校
    image(nodeImages[2], baseX + 160, baseY - 130);
    // A
    image(nodeImages[3], baseX + 30, baseY - 150);
    // B
    image(nodeImages[4], baseX + 280, baseY + 10);
    // C
    image(nodeImages[5], baseX + 310, baseY - 100);
}

// ノード名の描画
function drawNodeName() {
    textSize(20);
    text('家', baseX - 15, baseY + 50);
    text('お店', baseX + 115, baseY + 65);
    text('学校', baseX + 140, baseY - 165);
    text('A', baseX - 10, baseY - 150);
    text('B', baseX + 300, baseY + 40);
    text('C', baseX + 320, baseY - 110);
}

// 未訪問のノードのうち、コストが最小のものを調べて返す
function getMinNode() {
    // 未訪問のノードを調べる
    const unvisitedNodes = nodeMaps.filter((map) => {
        return !map.get('visited');
    });
    // 未訪問のノードのうちコストが最小のものを調べる
    const minNode = unvisitedNodes.reduce((a, b) => {
        if (a.get('cost') <= b.get('cost')) {
            return a;
        }
        else {
            return b;
        }
    });
    return minNode;
}

function setButton(label, pos) {
    const button = createButton(label);
    button.size(100, 30);
    button.position(pos.x, pos.y);
    return button;
}

下はアプリの実行画面です。select要素でスタート地点とゴール地点を設定し、[GO!]ボタンをクリックすると、２地点間の最短経路が赤線で示されます。