本稿は、毎日新聞の「プログラミング・はじめの一歩」とは関係のないオリジナル記事です。
目次
概要
本稿では、前の「31:番外編 円とサイン」で見たsin()やcos()関数を使って、三角形を描くときの考え方を探っていきます。
line()関数とtriangle()関数
p5.jsには図形の描画を行いやすくするための専用の関数が数多く提供されています。line()関数を使うと、2点を結ぶ線が描画でき、triangle()関数を使うと、3点を結ぶ三角形が描画できます。
const x1 = 30, y1 = 75, x2 = 58, y2 = 20, x3 = 86, y3 = 75;
// 3点をline()で結ぶ
line(x1, y1, x2, y2);
line(x2, y2, x3, y3);
line(x3, y3, x1, y1);
const offsetX = 70; // 右方向への移動量
// 3点を頂点とする三角形を描く
triangle(x1 + offsetX, y1, x2 + offsetX, y2, x3 + offsetX, y3);下図左はline()関数を、右はtriangle()関数を使った三角形の描画結果です。
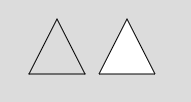
line()関数は2点を結ぶ線を描くだけなので、当然のことながら、三角形の内側は塗られません。これに対し、triangle()関数を使うと、辺で囲まれた部分を好みの色で塗ることができます。
3つの頂点を持つ三角形を描くだけならtriangle()関数に適当な3点の座標を指定すれば済みますが、三角形のとがった先を真上や真横に向かせるには、3点の座標の値を調整する、実際、triange()だけで二等辺三角形や正三角形を希望する位置に描くのは相当面倒です。そこで思いつくのが、円を描くときのサインとコサインです。
円と三角形
円は「7_6:円運動」の「サインとコサインと円」で述べているように、角度のコサイン値をx、サインをy値とする座標(x,y)の集まりです。
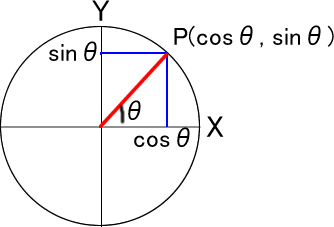
この点(x,y)は次の計算で求めることができます。
// (centerX, centerY)を中心とする半径がradiusの円
// 円周上のx座標値
const x = centerX + cos(angle) * radius;
// 円周上のy座標値
const y = centerY + sin(angle) * radius;cos()とsin()関数に渡す角度の値を変えると、その円周上にある異なる点が分かるので、点を3つ計算して、それらを頂点とする三角形を描くことができます。
不等辺三角形を描く
不等辺三角形とは、二等辺三角形でも正三角形でもない、3つの辺の長さが異なる、つまり適当に描ける三角形のことです。
点(centerX,centerY)を中心とする半径radiusの円の円周上にある3つの任意の点は、次のコードで決めることができます。
const rndNum = int(random(360));
const x = centerX + cos(rndNum) * radius;
const y = centerY + sin(rndNum) * radius;3つの点はtriangle()関数に与えると、三角形が描画できます。そのときには点(x,y)を[x,y]という配列に入れ、3つの点の配列を囲む2次元配列の使い勝手が良さそうです。次のdrawTriangle()関数では、[[x1,y1],[x2,y2],[x3,y3]]という2次元配列を受け取ることを前提としています。
// 三角形を描く。パラメータは3点の2次元配列
function drawTriangle(arr) {
fill(255); // 塗りを白にする
// 渡された2次元配列に含まれる3点を使って三角形を描く
triangle(arr[0][0], arr[0][1], arr[1][0], arr[1][1], arr[2][0], arr[2][1]);
}ランダムな3つの点を含んだ2次元配列を返す関数は、次のようなものが考えられます。
function getRandom3PointsOnCircle() {
let result = [];
for (let i = 0; i < 3; i++) {
const rndNum = int(random(360));
const x = centerX + cos(rndNum) * radius;
const y = centerY + sin(rndNum) * radius;
result.push([x, y]);
}
return result;
}次のコードでは、ボタンをクリックするたびに、新しい不等辺三角形が描画できます。
let centerX, centerY;
const radius = 100;
function setup() {
createCanvas(400, 300);
angleMode(DEGREES);
centerX = width / 2;
centerY = height / 2;
background(220);
// [描画]ボタン
const drawButton = setButton('描画', {
x: 300,
y: 270
});
drawButton.mousePressed(() => {
drawCircle();
const res = getRandom3PointsOnCircle();
drawTriangle(res);
});
}
// ランダムな角度で円周上の3点を作成して、それを入れた2次元配列を返す
function getRandom3PointsOnCircle() {
let result = [];
for (let i = 0; i < 3; i++) {
const rndNum = int(random(360));
const x = centerX + cos(rndNum) * radius;
const y = centerY + sin(rndNum) * radius;
result.push([x, y]);
}
return result;
}
// 三角形を描く。パラメータは3点の2次元配列
function drawTriangle(arr) {
fill(255); // 塗りを白にする
//fill(random(255), random(255), random(255));
// 渡された2次元配列に含まれる3点を使って三角形を描く
triangle(arr[0][0], arr[0][1], arr[1][0], arr[1][1], arr[2][0], arr[2][1]);
}
// p5.jsのellipse()関数で円を描く
function drawCircle() {
// 円はあくまでも補助なので塗りを背景色と同じにする
fill(220);
ellipse(centerX, centerY, radius * 2);
}
function setButton(label, pos) {
const button = createButton(label);
button.size(100, 30);
button.position(pos.x, pos.y);
return button;
}下はその実行画面です。
これを応用すると、不等辺三角形が連続して描かれ、全体の形状が円に見えるようになる面白い効果が作成できます。
let centerX, centerY;
const radius = 100;
let isAction = false;
function setup() {
createCanvas(400, 300);
angleMode(DEGREES);
centerX = width / 2;
centerY = height / 2;
background(220);
const res = getRandom3PointsOnCircle();
drawTriangle(res);
}
function draw() {
if (isAction) {
if (frameCount % 10 === 0) {
const res = getRandom3PointsOnCircle();
drawTriangle(res);
}
}
}
function mousePressed() {
isAction = !isAction;
}
// ランダムな角度で円周上の3点を作成して、それを入れた2次元配列を返す
function getRandom3PointsOnCircle() {
let result = [];
for (let i = 0; i < 3; i++) {
const rndNum = int(random(360));
const x = centerX + cos(rndNum) * radius;
const y = centerY + sin(rndNum) * radius;
result.push([x, y]);
}
return result;
}
// 三角形を描く。パラメータは3点の2次元配列
function drawTriangle(arr) {
//fill(255); // 塗りを白にする
fill(random(255), random(255), random(255));
// 渡された2次元配列に含まれる3点を使って三角形を描く
triangle(arr[0][0], arr[0][1], arr[1][0], arr[1][1], arr[2][0], arr[2][1]);
}下はこのコードの実行画面です。画面のクリックで動作のオン/オフが切り替えられます。
正三角形を描く
不等辺三角形は、円の円周上の点を3つランダムに選んで、その3点をtriangle()関数に渡すことで作成しました。では、正三角形を描画するには、どうすればよいでしょうか。
前の「番外編 円とサイン」の「円を描く」で述べているように、円周上の点の角度0は、円の真右の方向です。具体的に言うと、円の中心からx軸方向に進んだ、円周との交点の方向です。
正三角形の角の角度はどれも等しいので、この角度0をスタート地点とすると、120度ずつ時計回りに進んだ円周上の点を三角形の頂点にすれば、正三角形が描けるはずです。また、三角形のとがった先を真上に向けたい場合には、スタート地点を-90度にします。
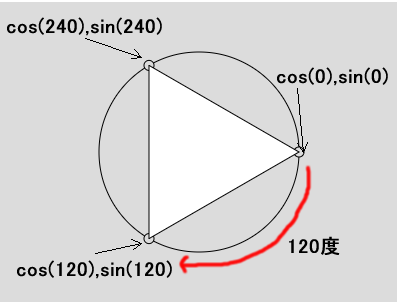
次のget3PointsOnCircle()関数は、渡された角度angleでの点(x1,y1)、そこから120度時計回りに進んだ点(x2,y2)、同じく240度進んだ点(x3,y3)を配列にまとめ、全体を2次元配列として返します。
function get3PointsOnCircle(angle) {
const x1 = centerX + cos(angle) * radius;
const y1 = centerY + sin(angle) * radius;
const x2 = centerX + cos(angle + 120) * radius;
const y2 = centerY + sin(angle + 120) * radius;
const x3 = centerX + cos(angle + 240) * radius;
const y3 = centerY + sin(angle + 240) * radius;
return [
[x1, y1],
[x2, y2],
[x3, y3]
];
}次の例では、画面をクリックすると、正三角形が次々に回転して描画されます。
let centerX, centerY;
const radius = 100;
let angle = -90;
let isAction = false;
const num = 13;
function setup() {
createCanvas(400, 300);
angleMode(DEGREES);
centerX = width / 2;
centerY = height / 2;
background(220);
const res = get3PointsOnCircle(angle);
drawTriangle(res);
}
function draw() {
if (isAction) {
if (frameCount % 10 === 0) {
const res = get3PointsOnCircle(angle);
drawTriangle(res);
}
angle += num;
}
}
/* 円に接する正三角形を想定すると、正三角形の頂点は、0度、120度、240度の位置にあると考えられる。
正三角形の上の頂点を真上方向に向けたい場合には、90度を引く
*/
function get3PointsOnCircle(angle) {
const x1 = centerX + cos(angle) * radius;
const y1 = centerY + sin(angle) * radius;
const x2 = centerX + cos(angle + 120) * radius;
const y2 = centerY + sin(angle + 120) * radius;
const x3 = centerX + cos(angle + 240) * radius;
const y3 = centerY + sin(angle + 240) * radius;
return [
[x1, y1],
[x2, y2],
[x3, y3]
];
}
// 三角形を描く。パラメータは3点の2次元配列
function drawTriangle(arr) {
fill(random(255), random(255), random(255));
// 渡された2次元配列に含まれる3点を使って三角形を描く
triangle(arr[0][0], arr[0][1], arr[1][0], arr[1][1], arr[2][0], arr[2][1]);
}
function mousePressed() {
isAction = !isAction;
}変数angleに数値を足すと、正三角形の頂点の位置を変えることができます。この数値の変数numに代入する値を変えると、結果として下図に示すような面白い結果が得られます。

二等辺三角形を描く
二等辺三角形を描くにあたって、わたしは次のように考えました。
- 三角形の1つの角が真上を向いていると、その頂点は(cos(-90),sin(-90))になる
- ここを基点に時計回りに-90+angle度進むと、(cos(-90+angle),sin(-90+angle))に着く
- 同様に反時計回りに-90-angle度進むと、(cos(-90-angle),sin(-90-angle))に着く
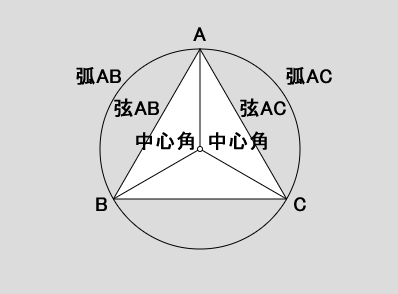
- 下図のAからC、AからBへ、方向は違えど同じ角度分だけ移動したのだから、ACとABの長さは同じになるはず
- 2辺の長さが等しければ二等辺三角形だと言える
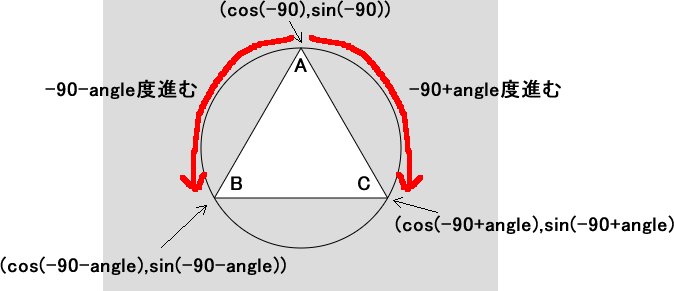
この考えの裏付けを取るべく、数学関係のWebページを調べて回り、円の中心角と弧、弦には、
- 等しい中心角に対する弧と弦の長さは等しい
- 等しい長さの弧に対する中心角と弦は等しい
- 等しい長さの弦に対する中心角と弧は等しい
という定理があることを見つけました(「円の中心角,弧,弦」)。
下図で言うと、弦ACと弦ABの長さは等しくなるので、三角形ABCは二等辺三角形だと言えるわけです。
この考え方は次のget6PointsOnCircle()関数でコード化できます。
function get6PointsOnCircle(angle) {
const x1 = centerX + cos(-90) * radius;
const y1 = centerY + sin(-90) * radius;
const x2 = centerX + cos(-90 + angle) * radius;
const y2 = centerY + sin(-90 + angle) * radius;
const x3 = centerX + cos(-90 - angle) * radius;
const y3 = centerY + sin(-90 - angle) * radius;
// 2点間の距離が等しいので二等辺三角形である
// print(dist(x1, y1, x2, y2));
// print(dist(x3, y3, x1, y1));
return [
[x1, y1],
[x2, y2],
[x3, y3]
];
}次のコードはget6PointsOnCircle()関数の使用例で、二等辺三角形を連続して描画します。
let centerX, centerY;
const radius = 100;
let angle = 90;
let isAction = false;
function setup() {
createCanvas(400, 300);
angleMode(DEGREES);
//noStroke();
centerX = width / 2;
centerY = height / 2;
background(220);
const res = get6PointsOnCircle(angle);
drawTriangle(res);
}
function draw() {
if (isAction) {
if (frameCount % 10 === 0) {
const res = get6PointsOnCircle(angle);
drawTriangle(res);
angle += 10;
}
}
}
function mousePressed() {
isAction = !isAction;
}
function get6PointsOnCircle(angle) {
const x1 = centerX + cos(-90) * radius;
const y1 = centerY + sin(-90) * radius;
const x2 = centerX + cos(-90 + angle) * radius;
const y2 = centerY + sin(-90 + angle) * radius;
const x3 = centerX + cos(-90 - angle) * radius;
const y3 = centerY + sin(-90 - angle) * radius;
// 2点間の距離が等しいので二等辺三角形である
// print(dist(x1, y1, x2, y2));
// print(dist(x3, y3, x1, y1));
return [
[x1, y1],
[x2, y2],
[x3, y3]
];
}
// 三角形を描く。パラメータは3点の2次元配列
function drawTriangle(arr) {
//fill(255); // 塗りを白にする
fill(random(255), random(255), random(255), 70);
// 渡された2次元配列に含まれる3点を使って三角形を描く
triangle(arr[0][0], arr[0][1], arr[1][0], arr[1][1], arr[2][0], arr[2][1]);
}画面のクリックで、二等辺三角形の連続描画のオン/オフを切り替えることができます。
N角形を描く
次のコードは、円周上の頂点を線で結ぶことでN角形を描画する例です。
// LineShapeオブジェクトを入れる配列
let ls = [];
function setup() {
createCanvas(400, 300);
angleMode(DEGREES);
}
function draw() {
background(220);
// ls配列に要素がある場合に
if (ls.length > 0) {
// LineShapeオブジェクトを描画
for (let i = 0; i < ls.length; i++) {
ls[i].drawShapeByLine();
}
}
}
// 画面のマウスプレスでLineShapeインスタンスを作成して配列に追加
function mousePressed() {
const num = int(random(3, 12)); // ランダムなN角形
const radius = int(random(5, 20)); // ランダムなサイズ
const lineShape = new LineShape(mouseX, mouseY, num, radius);
ls.push(lineShape);
}
class LineShape {
constructor(x, y, num, r) {
this.x = x; // 円の中心
this.y = y;
this.num = num; // N角形
this.angle = 360 / num; // 角度(360度をN等分)
this.radius = r; // 半径
this.color = color(random(255), random(255), random(255)); // カラー
}
drawShapeByLine() {
let arr = [];
//stroke(this.color);
fill(this.color);
// 円周上の(x,y)座標(N角形の頂点)を配列に入れ、(x,y)に小さな円を描く
for (let i = 0; i < 360; i += this.angle) {
const xpos = this.x + cos(i) * this.radius;
const ypos = this.y + sin(i) * this.radius;
arr.push([xpos, ypos]);
ellipse(xpos, ypos, 5, 5);
}
// N角形を描く(実際には頂点を線で結ぶ)
for (let i = 0; i < arr.length - 1; i++) {
line(arr[i][0], arr[i][1], arr[i + 1][0], arr[i + 1][1]);
}
line(arr[arr.length - 1][0], arr[arr.length - 1][1], arr[0][0], arr[0][1], )
}
}画面をクリックすると、クリックした位置を中心として、ランダムなN角形が描画されます。
星形
星形は三角形ではありませんが、sin()とcos()を使って大小2つの円を想定し、星形の頂点数の倍の点を結んでいくことで作成できます。詳細は「2:形(Form)」の「星形」で読むことができます。
以下はコードの例です。
let isAction = false;
let centerX, centerY;
let count = 0;
function setup() {
createCanvas(400, 300);
angleMode(DEGREES);
noStroke();
centerX = width / 2;
centerY = height / 2;
fill(random(255), random(255), random(255));
}
function draw() {
background(220);
if (isAction) {
translate(centerX, centerY);
rotate(count);
if (count % 60 === 0) {
fill(random(255), random(255), random(255));
}
star(0, 0, 30, 70, 5);
count++;
}
else {
translate(centerX, centerY);
rotate(count);
star(0, 0, 30, 70, 5);
}
}
function star(x, y, radius1, radius2, npoints) {
// 等分に刻む角度 =>外側の大きな円に使用
let angle = 360 / npoints;
// その半分の角度 => 内側の小さな円に使用
let halfAngle = angle / 2.0;
beginShape();
for (let a = 0; a < 360; a += angle) {
// 外側の大きな正npoints角形の頂点
let sx = x + cos(a) * radius2;
let sy = y + sin(a) * radius2;
vertex(sx, sy);
// 内側の小さな正npoints角形の頂点
// (sx, sy)は、時計回りの方向にhalfAngle分だけずれて、radius1の小さな円周上を移動する
sx = x + cos(a + halfAngle) * radius1;
sy = y + sin(a + halfAngle) * radius1;
vertex(sx, sy);
}
endShape(CLOSE);
}
function mousePressed() {
isAction = !isAction;
}下は実行画面です。画面のクリックで動作のオン/オフを切り替えることができます。

高校のプログラミング演習の参考にさせて頂きます。