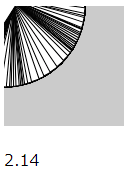
rotate()関数は座標システムを回転させます。引数には角度(ラジアン単位)を取り、(0, 0)に対しての、つまり原点を中心とした回転を作成します。
// 赤の矩形
fill(255, 0, 0);
rect(20, 20, 20, 40);
// 座標システムを反時計回りに15度回転
rotate(PI / 12.0); // => 15度
// 緑の矩形
fill(0, 255, 0);
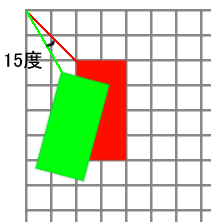
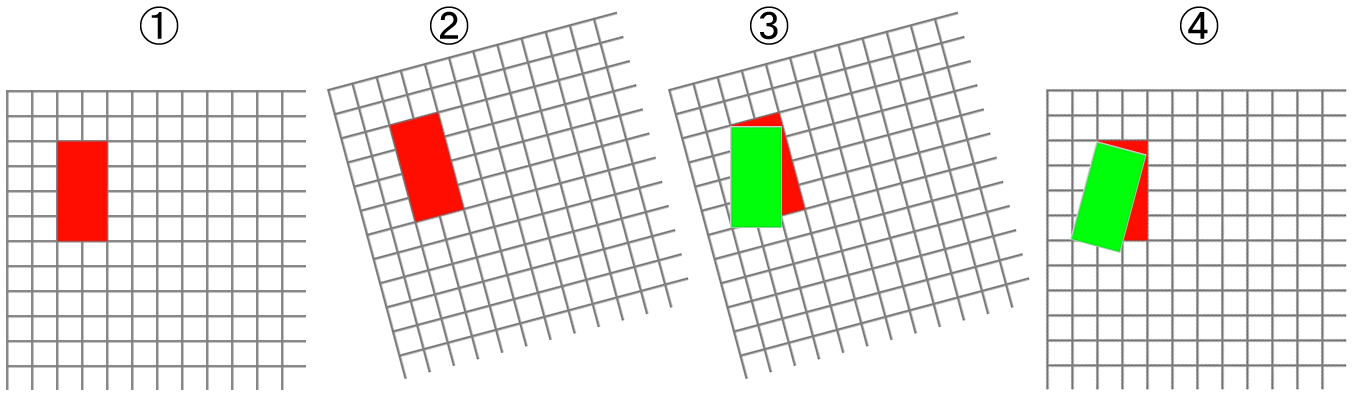
rect(20, 20, 20, 40);上記コードでは、比較のため、まず赤い矩形を作成し、その後座標軸を15度、反時計回りに回転させています。そして塗り色を緑にして、赤い矩形と同じ引数を与えてrect()を呼び出しています。下図からは、緑の矩形はキャンバスの原点と自身の左上隅とを結んだ直線によって、時計方向に15度、回ったように見えます。
ではこれを、移動のときと同様に、回転行列で行ってみます。点(x, y)を原点を中心に、反時計周りにθ度回転する計算は次の行列の掛け算で行います。
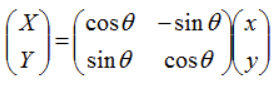
次のコードは、赤い矩形を描画した後、緑の矩形の4隅に相当する座標値を回転行列を使って変換し、その結果を黒い線で結びます。
// 回転させる角度(ラジアン単位)
const rad = PI / 12.0;
// 回転の変換行列
const RM = tf.tensor2d([cos(rad), -sin(rad), sin(rad), cos(rad)], [2, 2]);
RM.print();
// 矩形の4隅は(20,20),(40,20),(40,60),(20,60)
const xs = [20, 40, 40, 20];
const ys = [20, 20, 60, 60];
const result = xs.map((elm, index) => {
const m = tf.tensor2d([xs[index], ys[index]], [2, 1]);
return RM.matMul(m).dataSync();
});
print(result);
stroke(0);
strokeWeight(2);
line(result[0][0], result[0][1], result[1][0], result[1][1]);
line(result[1][0], result[1][1], result[2][0], result[2][1]);
line(result[2][0], result[2][1], result[3][0], result[3][1]);
line(result[3][0], result[3][1], result[0][0], result[0][1]);
下図に示すように、rotate()関数を使ったときと同様の結果が得られます。
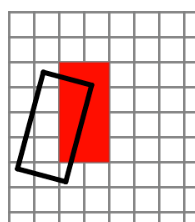
ところで、上記の回転行列は、座標軸を反時計回りに回転させますが、描画物が時計回りに回っているように見えます。これは次のように考えることができます。
- 赤い矩形を描画する。
- 座標軸を反時計回りに15度回転させる
- 回転させた座標軸で、緑の矩形を描画する
- しかし実際には、座標軸は水平と垂直方向でブラウザ画面に表示される
目次
rotate()
説明
シェイプをangleパラメータで指定された量だけ回転させる。この関数はangleModeを踏まえて動作するので、角度はRADIANSでもDEGREESでもどちらでも入力できる。
オブジェクトはつねに、原点に対する相対位置を中心に回転し、正数はオブジェクトを時計回りに回転させる。変換は、その後に発生するすべてのものに適用され、関数への以降の呼び出しによって効果が蓄積される。たとえば、rotate(HALF_PI)を呼び出しその後rotate(HALF_PI)を呼び出すことは、rotate(PI)と同じ。すべての変換はdraw()が新しく始まるときにリセットされる。
厳密に言うと、rotate()は回転行列と現在の変換行列を掛ける。この関数は、push()とpop()関数の使用によってさらに制御することができる。
シンタックス
rotate(angle, [axis])
sin()
説明
角度のサインを計算する。この関数は現在のangleModeを踏まえて動作する。返される値は-1から1までの範囲。
シンタックス
sin(angle)
cos()
説明
角度のコサインを計算する。この関数は現在のangleModeを踏まえて動作する。返される値は-1から1までの範囲。
シンタックス
cos(angle)
(0, 0)を中心としたシェイプの隅の回転
シェイプを回転させるには、まずrotate()で回転させる角度を決めます。描画はその後で行います。
let p;
function setup() {
createCanvas(120, 120);
background(204);
p = createP();
}
function draw() {
const angle = mouseX / 100.0;
rotate(angle);
p.html(angle);
rect(40, 30, 160, 20);
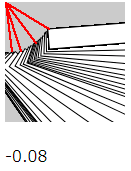
}マウスを動かすと、矩形の左上隅と原点とを結ぶ直線に振られるかのように矩形が動いて見え、矩形の左上隅の軌跡が原点を中心とした弧を描きます。
(0, 0)を中心としたシェイプのセンターの回転
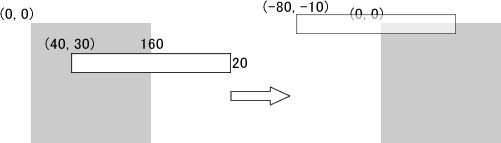
シェイプをそのセンターを中心に回転させるには、シェイプのセンターを(0, 0)に置いて描画する必要があります。下図に示す幅が160、高さが20の矩形を、そのセンターで回転させるには、矩形の左上隅から右に80、下に10進んだ矩形のセンターを、(0 ,0)に揃える必要があります。したがってこの矩形の左上隅は(-80, -10)の位置に来ることになります。
function draw() {
const angle = mouseX / 100.0;
rotate(angle);
p.html(angle);
// 矩形のセンターが(0, 0)と重なる位置に矩形を描画
rect(-80, -10, 160, 20);
}