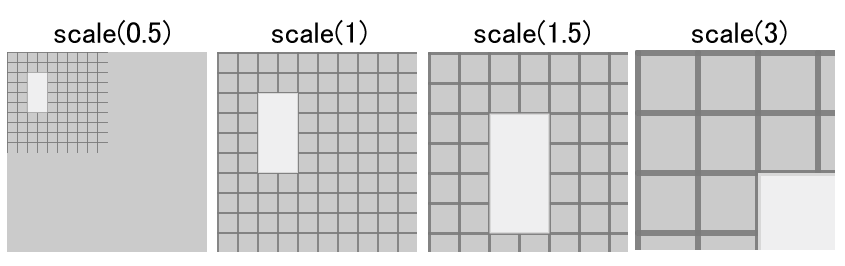
scale()関数はキャンバスの座標を引きのばしたり縮めたりします。スケール(縮尺比)の変化に合わせて、座標が伸縮するので、キャンバスの描画物すべてのサイズが大きくなったり小さくなったりします。スケールの量は小数点付きのパーセントで記述します。たとえばscale()のパラメータ1.5は150%に相当し、3は300%に相当します。
次のコードの変数scaleValにスケール値を指定すると、scale()関数の効果を目で確認することができます。グリッドを描画する前にscale()を実行しているので、グリッドも伸縮します。
function setup() {
const scaleVal = 1.5;
scale(scaleVal);
background(204);
// 10刻みのグリッドを描画
const step = 10;
for (let i = 0; i < width; i += step) {
for (let j = 0; j < height; j += step) {
stroke(125, 50);
strokeWeight(1);
line(i, 0, i, height);
line(0, j, width, j);
}
}
fill(240);
rect(20, 20, 20, 40);
}
点(x, y)を(0, 0)に関してX軸方向にSx倍、Y軸方向にSy倍する計算は次の行列の掛け算で行います。
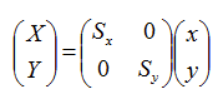
行列の扱いが得意なTensorFlow.jsライブラリを使って、計算してみます。変数SxとSyにスケール処理したい数値を代入します。
function setup() {
// x軸方向とy軸方向の倍率
const Sx = 1.5;
const Sy = 1.5;
// 拡大縮小の変換行列
const SM = tf.tensor2d([Sx, 0, 0, Sy], [2, 2]);
SM.print();
// 矩形の4隅は(20,20),(40,20),(40,60),(20,60)
const xs = [20, 40, 40, 20];
const ys = [20, 20, 60, 60];
const result = xs.map((elm, index) => {
const m = tf.tensor2d([xs[index], ys[index]], [2, 1]);
return SM.matMul(m).dataSync();
});
print(result);
background(204);
stroke(0);
strokeWeight(2);;
line(result[0][0], result[0][1], result[1][0], result[1][1]);
line(result[1][0], result[1][1], result[2][0], result[2][1]);
line(result[2][0], result[2][1], result[3][0], result[3][1]);
line(result[3][0], result[3][1], result[0][0], result[0][1]);
}scale()関数を使ったときと同様の結果が得られました。
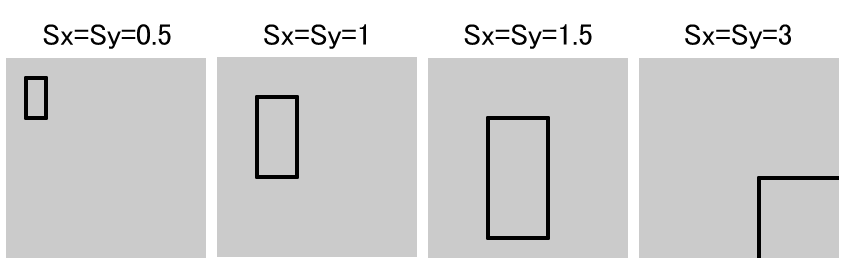
目次
scale()
説明
頂点を伸縮させることでシェイプのサイズを拡大または縮小する。対象物はつねに、座標システムに相対的な原点から伸縮する。スケール値は小数点付きパーセンテージとして指定する。たとえば関数呼び出しscale(2.0)はシェイプのサイズを200%大きくする。
変換は累積的に作用する。その後に発生するすべてのものに適用され、関数への以降の呼び出しによって効果が蓄積される。たとえばscale(2.0)を呼び出しその後scale(1.5)を呼び出すことは、scale(3.0)と同じ。draw()内でscale()を呼び出すと、変換は、次のループが始まるときにリセットされる
zパラメータはWEBGLモードが有効な場合のみ。この関数は、push()とpop()関数の使用によってさらに制御することができる。
シンタックス
scale(s, [y], [z])
scale(scales)
スケーリング
scale()関数は、rotate()と同様、変換を原点から実行します。
let p;
function setup() {
createCanvas(120, 120);
p = createP();
background(204);
fill(255, 255, 0);
}
function draw() {
// 矩形のサイズはmouseXに比例する
scale(mouseX / 60.0);
rect(0, 0, 30, 30);
p.html(mouseX / 60.0);
}(mouseX / 60.0)はマウスが右へ行くほど大きく、左へ行くほど小さくなるので、描かれる矩形のサイズもそれに比例します。このとき矩形は左上隅が原点と重なった状態で拡大縮小します。

したがって、シェイプをそのセンターから拡大縮小したいときには、rotate()のときと同じように、一度その位置に移動し、それから拡大縮小して、シェイプのセンターを(0, 0)に置いて描画します。
function draw() {
// 矩形はマウスに追随する
translate(mouseX, mouseY);
// 矩形のサイズはmouseXに比例する
scale(mouseX / 60.0);
rect(-15, -15, 30, 30);
p.html(mouseX / 60.0);
}
とはいえ、いちいちrect(-15, -15, 30, 30)の-15などを計算するのは面倒なので、setup()内でrectMode(CENTER)を実行し、draw()でrect(0, 0, 30, 30)を呼び出す方が簡単です。
線の太さを維持する
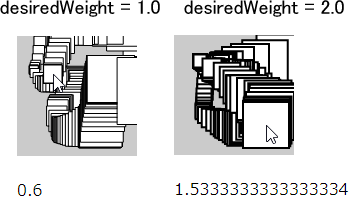
scale()関数による拡大は線の太さ(ストロークの重み)にも影響するので、シェイプが大きくなると線も太くなります。線の太さを一定にしたい場合には、希望するストロークの重みを実数値で割ります。
let p;
const desiredWeight = 1.0;
function setup() {
createCanvas(120, 120);
rectMode(CENTER);
p = createP()
background(204);
}
function draw() {
translate(mouseX, mouseY);
// 実数
const scalar = mouseX / 60.0;
p.html(scalar)
scale(scalar);
// 線の太さをdesiredWeightに維持する
strokeWeight(desiredWeight / scalar);
rect(0, 0, 30, 30);
}
p5.jsのScaleサンプル解説
p5.jsの「Scale」ページにはscale()関数のサンプルコードが公開されています。以下はその解説です。
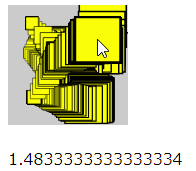
このサンプルをブラウザで実行すると、白と黒の矩形が左右に移動し、大きくなったり小さくなったりします。よく見ると、白の方が左右への移動量が多く、拡大率も大きいことが分かります。そして何より、2つの矩形は同じことをずっと繰り返します。
変数aとs
移動はtranslate()に、拡大縮小はscale()に行わせるのは想像できますが、ずっと同じことを継続して行わせるには、そういう数値をずっと与える必要があります。aとsはそういう数値の作成に関係する変数です。
aもsも最初、0に初期化されています。setup()とdraw()関数の外で作成されているので、setup()の中からも、draw()の中からもアクセスできます。
let a = 0.0;
let s = 0.0;draw()内でaはほんの少しずつ大きくなっています。sはこのaのコサイン値の2倍になります。
// aは少しずつ大きくなる。
a = a + 0.04;
// このaのコサインを使って滑らかな周期運動を作成する
s = cos(a) * 2;コサインと聞くと、いきなり頭の中が真っ白になるかもしれません。そういうときは具体化してみるのがよい方法です。具体化とは、たとえば具体的な数値を割り当てて、それらが結果にどのように影響するかを観察する、というようなことです。また視覚化も理解に役立ちます。
plotly.jsというライブラリでaとsを視覚化すると、次のようになります。
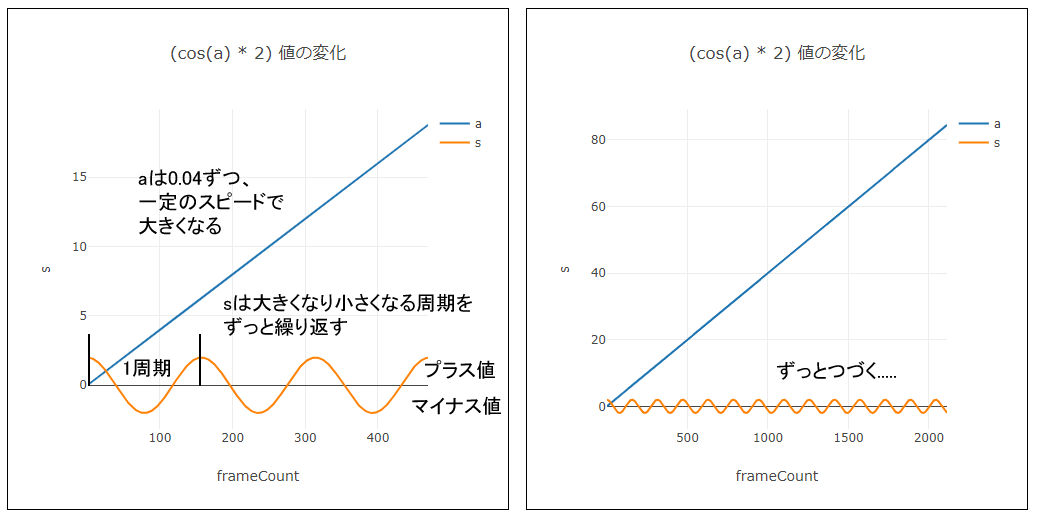
aは欲しいsを生み出すためにcos()に与えるネタです。ごく微量ずつ大きくすることで、得られるsの変化も微量になります。sは2を掛けてはいますが、要するにaのコサイン値です。2はsを倍にする働きを持ちます。
sは、
- 2から始まり滑らかに-2まで小さくなる。0までは正数で、その後は負数
- -2を境に滑らかに2まで大きくなる。0までは負数で、その後は正数
を1周期として、ずっと繰り返します。このsをscale()に適用すると、滑らかな拡大縮小を延々繰り返すアニメーションが作成できます。
黒の矩形
sの変化が分かったので、黒の矩形を描画してみます。
let a = 0.0;
let s = 0.0;
function setup() {
createCanvas(720, 400);
noStroke();
rectMode(CENTER);
}
function draw() {
background(102);
// aは少しずつ大きくなる。
a = a + 0.04;
// このaのコサインを使って滑らかな周期運動を作成する
s = cos(a) * 2;
// 原点からキャンバスのセンターに移動
translate(width / 2, height / 2);
// sでスケール => sは滑らかな周期運動なので、滑らかな拡大縮小を繰り返す
scale(s);
fill(51);
rect(0, 0, 50, 50);
}ここではtranslate(width / 2, height / 2)で座標軸をキャンバスのセンターに移動させてから、scale(s)を呼び出し、矩形のセンターを(0, 0)として描画しています。これらを記述したdraw()関数は1秒間に60回呼び出され、sは微小に変化するので、キャンバスには矩形が滑らかに拡大縮小をつづけるアニメーションが描かれます。

白の矩形
次は白の矩形の描画です。
// 移動と拡大縮小の変換は累積するので、この移動は2つめの白い矩形を1つめより遠くに移動し、
// 拡大縮小の効果も2倍になる。
// sはコサインによって正負両方の値になるので、左右を往復する動きになる。
translate(75, 0);
fill(255);
scale(s);
rect(0, 0, 50, 50);translate(75, 0)は座標軸を右に75移動させますが、これは前のtranslate(width / 2, height / 2)に累積されて適用されるので、translate(75, 0)以降の矩形は(width /2 + 75, height / 2)をそのセンターとして描画されることになります。この累積は拡大縮小でも同様で、白い矩形にはscale(s)が2回適用され、結果として、白い矩形は黒い矩形よりも多く移動し、大きく拡大されることになります。

